大学物理光的干涉

大学物理光的干涉

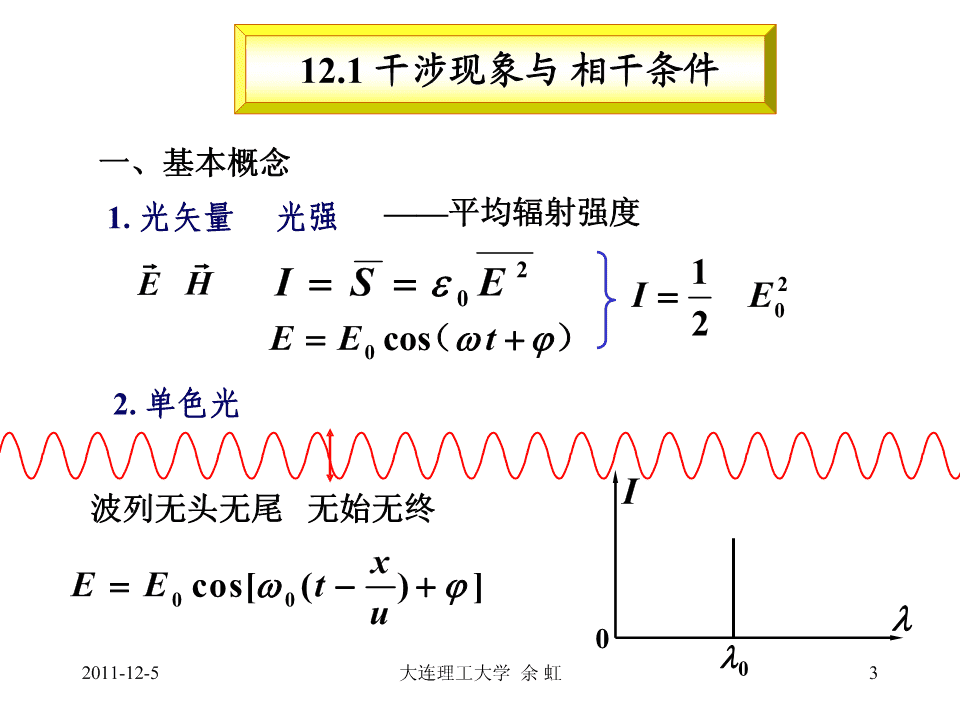
第11章几何光学的基本概念第12章光的干涉第13章光的衍射第14章光的偏振第15章光与物质相互作用2011-12-5大连理工大学余虹1\n12.1干涉现象与相干条件12.2杨氏双缝干涉12.3光的时空相干性12.4分振幅干涉12.5迈克尔孙干涉仪2011-12-5大连理工大学余虹2\n12.1干涉现象与相干条件一、基本概念1.光矢量光强——平均辐射强度21EHISEIE20002EEcos（t）02.单色光I波列无头无尾无始无终xEEcos[(t)]00u002011-12-5大连理工大学余虹3\n3.复色光准单色光实际波列有限长——复色光间断振动一般原子发光810s0I准单色光1410Hz8c310m/s波列长度lc0000波列越长单色性越好准单色光：002011-12-5大连理工大学余虹4\n二、相干光和相干条件我开了两盏灯,1.波的独立性原理和叠加原理为什么没看见干涉条纹？光的干涉是有条件的！EEES122S12011-12-5大连理工大学余虹5\n——I不处处为0的条件122.相干条件在交叠区(1)相同EE1E2(2)夹角E12E不随t变化，π且222(EI1EE2)?(3)相位差是常量(不随时22间变化）EE2EE1212III干涉项1212若I处处为012IEEcoscos121020非相干叠加2IIcos12I=I+I122011-12-5大连理工大学余虹6\n3.相干叠加光强分布只是空间的函III2IIcos数，因此光强在空1212间呈稳定分布。在=2k处k=0，1，2，…当III120III2IIM1212II4在=(2k1)处k=1，2，…M0I0mIII2IIm1212原子发光具有随机性、间断性，即使同一个原子发出的前后两列波，也很难保证同时满足三个相干条件。要获得相干光需要采取特殊的方法。2011-12-5大连理工大学余虹7\n4.获得相干光的主要方法分波阵面法——具有确定相分振幅干涉法——透射位差的波阵面上的两个次级光与反射光子光源WW反入W透WWW入反透2WE02011-12-5大连理工大学余虹8\n12.2杨氏双缝干涉x一、现象rxsn11SIrd2OsD2条件:dDxDEEEcostS1S20r1EEcos(t)10ur2EEcos(t)202011-12-5大连理工大学余虹u9\nIII2IIcos二、光强分布1212x当缝宽相等III120()rrsnr1x12121udr2O2πsO()rr212Du2π()rrnr121E1EE00cos(cos(tt1))nur12πr12uEEEcoscos((t))2002u=2k(0k,1,)kIM4I0（明）0=（2k1）(2k1)I（暗）2m(1k,2,)2011-12-5大连理工大学余虹10\n三、条纹位置xk明r1x（）21k暗sn21dr2r2r1s2hdsinshodDx2DsintanxDDxndxndk明条纹中心：kn(rr)21DDDxk(0k,1,2)knd条纹间距：暗条纹中心：DDxxk(2－1)(k1,2,)knd2nd2011-12-5大连理工大学余虹11\n例题杨氏双缝实验，=500nm，在一光路中插入玻璃片（n=1.5）后O点变为4级明纹中心。求：玻璃片厚度e。解：光程差改变neex条纹移动N=4(e,n)sN1ONes2n14n14000nm2011-12-5大连理工大学余虹12\n四、洛埃镜实验nr1直射光光程nr1r2反射光光程nr2a22Dk明k=0,1,2……n(rr)212（）21k暗k=1,2……2思考与杨氏双缝实验比干涉条纹有哪些相同、不同之处？2011-12-5大连理工大学余虹13\n12.3光的时空相干性一、准单色光的谱线宽度——与时间相关原子发光持续时间为波列长度Lc有限(视为)无限长波列的集合越长L越长集合中的波列越少单色性越好II单色光准单色光0I02光强降到一半时曲线的宽度——谱线宽度0000222011-12-5大连理工大学余虹14\n二、时间相干性I1.准单色光双缝干涉条纹IM0I/2M102202单色光双缝干涉I总光强Dxndx2级条纹开始消失不同波长——非相干叠加——光强叠加发光时间对干涉条纹清晰度的影响——时间相干性2011-12-5大连理工大学余虹15\n2.相干长度第k级由于光源的非单色性,202重合k级以上条纹消失！第k+1级102()k()(k)10022kkkk000222k200相干长度第k级明条Mk纹的光程差M0相干长度～谱线宽度～原子发光持续时间都描述时间相干性2011-12-5大连理工大学余虹16\n三、空间相干性光源的空间拓展对干涉条纹清晰度的影响R2当RR12bd2sR1RD光强叠加的结果干涉条纹消失22db2R22RbdRR()12122bdbd()RRRRb()ddb1212222RRR2RR()12222bdR0b光源宽度极限b002R2d光源宽度越是小于b0d令称相干孔径相干性越好R2011-12-5大连理工大学余虹17\n12.4分振幅干涉一、等倾干涉1.等倾干涉相长与相消的条件ABcosih22ABnADnADACsini121SLACitan22h22hnhn1sini2222hni22t2thihinin1122aann22sinsinsini2coscosii22cosi2csoi2in1D2hncosi122kA（明）Cnh22222hnnsini()=B211(2k1)n223i（暗）2n1n2n3n1n2n3考虑半波损失2011-12-5大连理工大学余虹18\n2.等倾干涉的特点SL1.倾角相同的光线形成的干涉光光强相同。i2.所有的平行光汇聚在透镜焦平面1n上的同一点。使条纹的对比度更1高。n2h3.透镜正放，焦面上条纹是一组n同心圆。3问题：透射光的干涉情况如何？2011-12-5大连理工大学余虹19\n二、等厚干涉1.劈尖薄膜的等厚干涉(1i0nn)113k明2hn2k暗2(2kk1)(12,明)2hn2kk（,012,）暗h第m条暗纹对应膜厚hk厚度差hhh相邻kk12n两条纹h中心间距llsin2n2011-12-5大连理工大学余虹20\n例题白光照射空气中的平行薄膜，已知h=0.34m，n=1.33问：当视线与膜法线成60º和30º时观察点各呈什么颜色？222解2hnnsinim21122260o30o2hnsini2(m)112hnoi6014576.nmm2224hnsini1oi302m115587.nmm12011-12-5大连理工大学余虹21\n2.等厚干涉的应用(1)增透膜与增反膜玻璃（n=1.5）镀MgF（n=1.38），放在空气中，白322光垂直射到膜的表面，欲使反射光中=550nm的成分相消，求：膜的最小厚度。nnn123n112(hn21k)相消2hn.13822n35.12hnk2hk24n2反射光相消=增透思考：若n>n会得23效果最好——nnn213到什么结果？2011-12-5大连理工大学余虹22\n(2)测长度微小变化(3)检查光学平面的缺陷玻璃板向上平移动移纹条温度升高涉干相邻两条纹中h条纹偏向膜（空气）厚部表心对应高度差2示平面上有凸起。条纹整体移NHN根，高度变化2H平面上有凹坑。材料膨胀系数T2011-12-5大连理工大学余虹23\n(4)测凸透镜的曲率半径/见大学物理实验k明2hn221k暗2中心hk00暗半径rRhRk第k级暗环对应k膜厚hkr2nh222RR()hrkk2222Rhhrrkkkk牛特点顿2级次—内低外高nrk环R间距—内疏外密k2011-12-5大连理工大学余虹24\n(5)牛顿环在光学冷加工中的应用压压环外扩：要打磨中央部分环内缩：要打磨边缘部分2011-12-5大连理工大学余虹25\n12.5迈克尔孙干涉仪/见大学物理实验nnn1123M1MM//M1h12MM22实现等倾干涉ii12k明2h/cosii21M(2k1)暗12M条为动镜1注意：h~k为增函数条纹特点1.同心圆望远镜2h2.内疏外密m03.中心明暗不定上式成立时为明纹级次m02011-12-5大连理工大学余虹26\n2hm0平移Mh变化条纹分布变化1M1更高级次的环从M2h~k为增函数中心“涌出”，所有hk的环都往外扩。原最高级次的环hki1M1从中心“缩进”，所有的环都往里缩。2h变化，条纹集体移一个间距。望远镜h0条纹消失！hN22hLc劈尖（n）插入，条纹移N根，厚度？2011-12-5大连理工大学余虹27