大学物理课件 (1)

大学物理课件 (1)

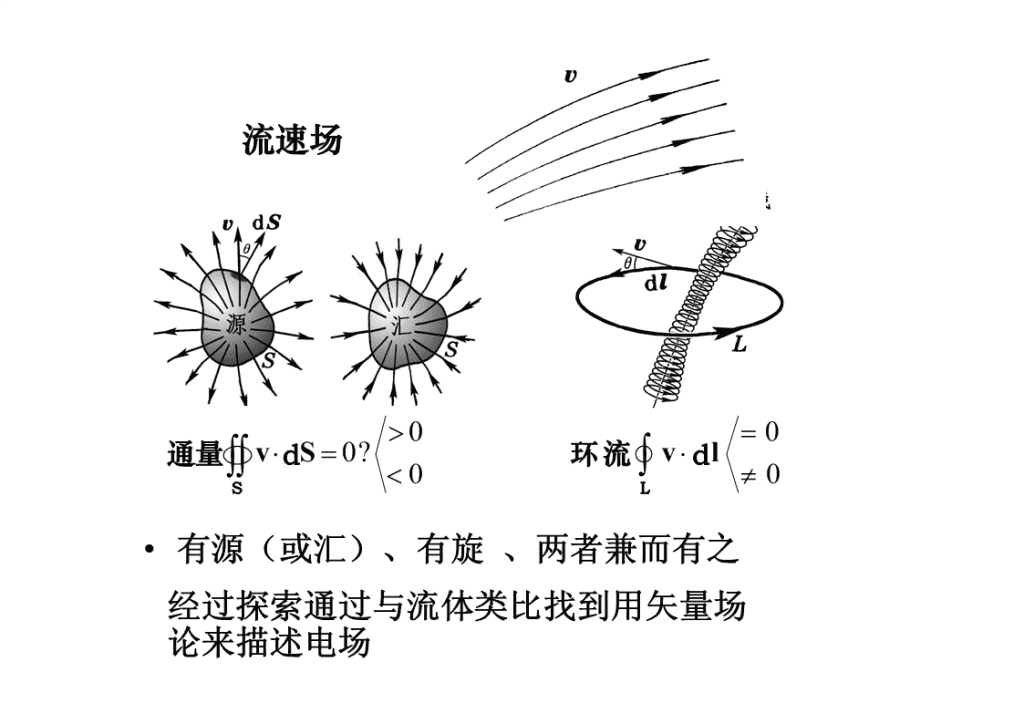
期中考试时间：第九周周五（4月20日18:30）内容：力学、相对论、静电学（前五章，14章）第九周周四停课\n例6.一半径为R的均匀带电半球面。其面电荷密度为，求该半球面球心处的电场强度大小。解：今取一半径为r，宽度为Rdr的带电细圆环hhdqoddEhRcos34R0dq2rRd()2(sin)(RRd)32RsincosddEsincosd34R2002整个半球面EdEsincosd02400\n流速场00通量vdS0?环流vdl00SL•有源（或汇）、有旋、两者兼而有之经过探索通过与流体类比找到用矢量场论来描述电场\n§5―4电场强度通量高斯定理一电场线1.电场线：描述电场分布情况的曲线。⑴曲线上每一点的切线方向表示该点电场强度E方向。⑵曲线的疏密表示该点处场强E的大小。即：通过电场中某点垂直于E的单位面积的电场线数，在数值上就等于该点处电场强度的大小。dNdSEEdS电场线密度\n2.几种常见的电场线：正点电荷负点电荷+\n一对等量正点电荷的电场线++\n一对等量异号点电荷的电场线+\n带电平行板电容器的电场线++++++++++++3.静电场中电场线的特点：⑴电场线起始于正电荷，终止于负电荷。⑵电场线不闭合，不相交。⑶电场线密集处电场强，电场线稀疏处电场弱。\n二电场强度通量电场强度通量（电通量）e—通过电场中任一曲面的电场线条数。1、均匀电场中通过平面S的电通量SSnnEEeESeEScosES\n2、非均匀电场的电通量nEdEcosdSEdSdSEcosdSEdSeSSS对闭合曲面的电通量：nEcosdSEdSθEeSSθn规定：外法线方向为正S（1）当<90°时：电场线穿出闭合曲面，电通量为正（2）当>90°时：场电线穿进闭合曲面，电通量为负（3）当=90°时：电场线与曲面相切，电通量为零\n例1.有一三棱柱放在电场强度为E=200N·C-1的均匀电场中。求通过此三棱柱的电场强度通量。解：ynEScosESθ111nEθS5S01ox234S4zSSEScosES3n2551012345\n三高斯定理1.高斯定理的表述和表达式：在真空中，通过任一闭合曲面的电场强度通量等于该曲面所包围的所有电荷的代数和的1/倍。o此闭合曲面—高斯面E1nineEdSqiSoi1SdS2.高斯定理的证明：+R⑴点电荷在球形高斯面的球心处qE2dEcos0dS4ReoqdSq2q4ReS224R4Rooo\n⑵点电荷在任意形状的高斯面内E通过球面S的电场线也必通过任意曲面S′，即它S'S++们的电通量相等,为q/o。qEdSeSo⑶点电荷在高斯面以外ES)穿进曲面的电场线条数n等于穿出曲面的电场线条数。(EdS0＋eS\n(4)高斯面内含有任意电荷系—点电荷的集合体1nineSEdSSEdSiqiq1i0i1q2qq讨论：n(1)高斯定理是电磁理论的基本方程。(2)高斯面是一闭合曲面。(3)电场强度通量不等于零，说明静电场是有源场。(4)E是总场，由高斯面内外电荷决定。只由内部电荷决定。e\n四高斯定理的应用（用高斯定理求解的静电场必须具有一定的对称性）其步骤为对称性分析；根据对称性选择合适的高斯面；应用高斯定理计算.\n例1.求均匀带电球壳的场强分布。（已知薄球壳半径为R，带电量为Q）解：由于电荷分布球对称，则场强分布球对称。场中任意点场强方向沿径矢，球面上各点场强大小相等。QRqiE由高斯定理：EdSOrPS在r>R处0Q2高斯面EdSEdSEdSE4rSSSE0QQEEe22r4r4r00OEdSEr2Rr在rRErR2qq12qqE2122EdSEdSE4r40rSS0\n例6.无限长的同轴圆柱与圆筒均匀带电。圆柱的半径为R，其电荷体密度为，圆筒的内外半径分别11为R和R（R＜R＜R）其电荷体密度为，求空间231232任一点的电场强度？R解：场强具有轴对称性，由高斯定R12理解题，取圆柱面为高斯面。R3q12iEdSr⑴r＜RSl1012EdSE2rlrl1S0r1E⑵R1＜r＜R220122EdSE2rlR1l1E1R1S02r0\n⑶R＜r＜R23RR12EdSE2rlR3S121222Rl(rR)l2r112l01222ER11(rR2)21122r0⑷r>R3EdSE2rlS1222222ER(RR)2R1l1(R3R2)l211322r0\n由高斯定理求解场强：1均匀带电球类2无限长均匀带电直线类3无限大均匀带电平面类