大学物理热力学

大学物理热力学

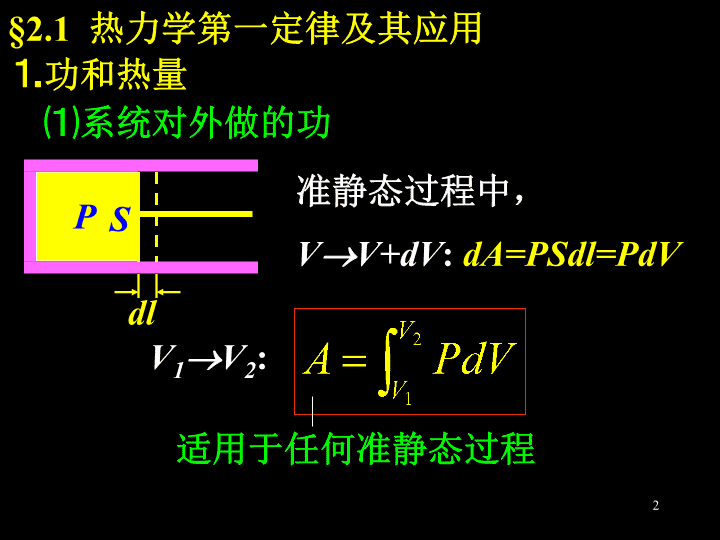
第二章热力学第一定律(TheFirstLawofThermodynamics)主要内容：热力学第一定律等体过程等压过程等温过程绝热过程循环过程卡诺循环1\n§2.1热力学第一定律及其应用⒈功和热量⑴系统对外做的功PSdl准静态过程中，VV+dV:dA=PSdl=PdVV1V2:适用于任何准静态过程2\nPV12AV2V1ONotes:①功是过程量,其值依赖于过程.②功还可通过热Ⅰ律计算。3\n⑵系统吸收的热量准静态过程中,TT+dT:Notes:①C是过程量,其量值依赖于过程.e.g.绝热压缩过程：dQ=0,dT>0C=0等温膨胀过程：dQ>0,dT=0C系统在该过程中的摩尔热容4\n③Q也是过程量.②若过程中C=const.，则有e.g.等体过程：等压过程：④Q还可通过热Ⅰ律计算。5\n⒉热力学第一定律⑴无限小过程：dQ=dE+dAdQ——系统吸收的热量dE——系统内能的增量dA——系统对外做的功⑵有限过程：Q=（E2-E1）+A6\nNotes:①E是状态量。理想气体：PV12Oab状态1状态2：E2-E1确定，过程不同，A不同，Q也就不同7\n②热Ⅰ律本质：能量守恒。它普遍适用于任何系统(固、液、气)的任何过程(准静态或非准静态)。⒊等体过程(isochoricprocess)V=const.dA=0,dQ=dEPV12O8\n由摩尔定体热容得——常量于是(适用于等体过程)(适用于任何过程)9\n⒋等压过程(isobaricprocess)P=const.dQ=dE+dAPV12O因摩尔定压热容10\n故有——迈耶(Mayer)公式or——常量于是此外11\n仅适用于等压过程因此⒌等温过程(isothermalprocess)T=const.dE=0,dQ=dAPV12O12\n13\n⒍绝热过程(adiabaticprocess)dQ=0dE+dA=0PV12Oisothermadiabat推导：约束条件(dQ=0)＋状态方程⑴绝热过程方程14\n①②①②→③——比热容比其中(ratioofspecificheat)15\n对③积分，得——泊松(Poisson)公式④利用状态方程，又可得⑥⑤④⑤⑥——绝热过程方程。C1,C2,C3是常量16\nNote:绝热过程方程是状态方程在绝热过程中退化的结果，在其它典型过程中也有类似的形式.e.g.等体过程：等温过程：等压过程：17\n⑵绝热过程中功的计算此外，若(E2-E1)易求，则A=(E2-E1)⒎绝热自由膨胀(freeexpansion)P1,V1T1P2,V2,T2该过程不是准静态过程,但仍服从热Ⅰ律.18\n绝热→Q=0自由膨胀→A=0E2E1=0T2=T1PV12Oisotherm19\n§2.2循环过程(CyclicProcess)——系统经历一系列变化后又回到初态的整个过程。正循环(A>0)——热机逆循环(A<0)——致冷机PVOA20\nQ1Q2A高温热库T1低温热库T2系统⒈热机的效率在一个循环中：系统从T1吸热量——Q1向T2放热量——Q2对外做功——A热Ⅰ→Q1Q2=A热机的效率：21\ne.g.Steamlocomotive=8%gasolineengine25%Dieselengine37%steamturbine46%Note:通常,Q1=Q1i,Q2=Q2i.[例2-1]双原子理想气体作如图的循环，V2/V1=2，求.PVacObV1V2isotherm22\n解：Q1=Qab+QbcQ2=Qca其中ab——等体升压(吸热)bc——等温膨胀(吸热)ca——等压压缩(放热)23\n其中于是因此24\n⒉致冷机的致冷系数高温热库T1低温热库T2系统在一个循环中：系统从T2吸热量——向T1放热量——外界对系统做功——热Ⅰ→25\n致冷系数：通常w>1⒊卡诺循环(Carnotcycle)S.Carnot(1796~1832),Frenchengineer1824年，提出Carnotcycle.26\nCarnotcycle:由两条等温线和两条绝热线构成。正循环——卡诺热机逆循环——卡诺致冷机⑴卡诺热机(Carnotengine)PVT1T2Odabc27\n证：又，对于状态b和c，有对于状态a和d，有于是28\nNote:上式实际上对于任意工质的卡诺热机都成立。[思考]①在卡诺循环中，两条等温线下的面积是否相等？为什么？②两条绝热线下的面积是否相等？物理意义？因此29\n[例2-2]1mol理想气体作卡诺循环，T1=400k，T2=300k，在400k的等温线上起始体积V1=0.001m3，终止体积V2=0.005m3，求气体在每一循环中①从高温热源吸收的热量Q1；②所做净功A；③传给低温热源的热量Q2。解：PVT1T2OdabcV1V2①30\n②③31\n(自证)Note:上式实际上对于任意工质的卡诺致冷机都成立。⑵卡诺致冷机(Carnotrefrigerator)32\nSUMMARY⒈系统对外做功——过程量⒉系统吸热——过程量⒊理想气体内能增量——取决于始末态33\n⒋热Ⅰ律dQ=dE+dAQ=(E2-E1)+A⒌等体过程A=0Q=E⒍等压过程34\n⒎等温过程E=0⒏绝热过程Q=0E+A=0——绝热过程方程35\n⒐绝热自由膨胀——非准静态过程Q=A=E=0T2=T1⒑热机效率卡诺热机：⒒致冷机的致冷系数卡诺致冷机：36\nEXERCISES⒈理想气体的状态变化遵从PV2=B的规律(B为正常数)，则当体积由V1膨胀至2V1时，气体对外做功A=。解：[思考]设气体分子自由度为i,则E=?Q=?37\n解：⒉某理想气体的比热容比＝7/5，处于温度为T的平衡态，则该气体的定容摩尔热容量CV=；一个分子的平均转动动能。⑴38\n[思考]若已知一个分子的平均转动动能为,则=?Cv=?⑵∵分子的转动自由度为5-3=239\n⒊1mol的理想气体在等压过程中温度上升1k，内能增加20.78J，则气体对外做功为，气体吸收热量为。解：⑴⑵[思考]①其它解法？②若为等体过程，结果？③若为绝热过程，结果？40\n答：⒋如图，MT为等温线，MQ为绝热线，则在AM,BM,CM三种准静态过程中，温度升高的是过程；气体吸热的是过程。⑴BM,CM理由：(TB,TC)0Q>0(吸热)但Q=QCM+QQC而QQC<0(放热)故QCM>0(吸热)PVACOBMTQ41\n[思考]①P-V图上等温线两侧的温度分布有何特点？②对本题第二问的其它分析方法？类似地，可判定BM,AM是放热过程。42\n解：⒌一定量的氮气经绝热压缩,压强变为原来的2倍,问气体分子平均速率变为原来的几倍？(A)(B)(C)(D)[]由绝热过程方程知43\n[思考]①方均根速率是原来的几倍？②若为单原子或多原子气体,结果？③若氮气经绝热压缩,体积变为原来的1/2,结果？故44\n⒍理想气体初态为(T,V)，绝热膨胀到2V，再经等容过程使温度恢复为T，再经等温过程压缩到原体积V，则在此循环过程中(A)气体向外界放热.(B)气体对外界做功.(C)气体内能增加.(D)不确定.[]解：PVOV2V此为逆循环，A<0Q<0（放热）(A)[思考](B)(C)为什么不对？45\n⒎一定量的理想气体经历如图所示的循环过程，其中ab、cd是绝热过程，则该循环的效率=.解：该循环是卡诺循环，故P(atm)T(k)O3004005abcd[思考]为什么该循环对应于卡诺热机而不是卡诺致冷机？46\n⒏总容积为40l的绝热容器中间有一绝热隔板，其重量忽略，可无摩擦地升降。A、B两部分各有1mol的氮气，初压强均为1.013105Pa，初始时隔板停在容器正中间。现在使微小的电流通过B中的电阻缓缓加热，直到A部气体体积缩小到一半。求在此过程中：⑴A部气体经历了什么过程？⑵A、B两部分气体各自的最后温度。⑶B中气体吸收的热量。IAB47\n解：⑴绝热压缩；⑵A部：初态温度由绝热过程方程,得末态温度：48\nB部：末态压强末态温度：⑶热Ⅰ→QB=EB+AB其中EB=CV(TB2-TB1)=CV(TB2-TA1)AB=EA=CV(TA2-TA1)49\n于是[思考]“隔板重量忽略”、“可无摩擦地升降”、“缓缓加热”各意味着什么？50