大学物理16-2

大学物理16-2

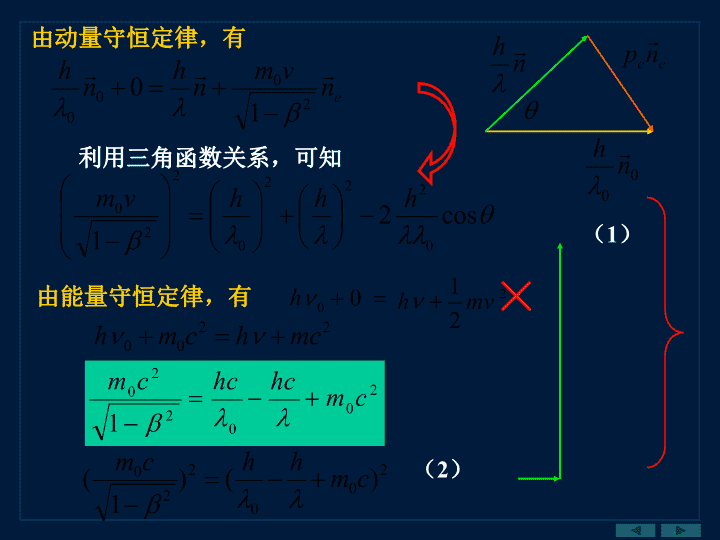
UniversityPhysicsQuantum2\n黑体——1.斯特藩——玻耳兹曼定律2.维恩位移定律黑体辐射的基本规律和普朗克的能量子假设普朗克的能量子假设h=6.63×10-34J·s=h能够全部吸收各种波长的辐射能的物体光电效应方程\n由动量守恒定律，有利用三角函数关系，可知由能量守恒定律，有（1）（2）\n康普顿效应公式康普顿波长讨论：(1)波长差与散射物质的种类、与入射光的波长无关。(2)在可见光范围内，——康普顿效应主要显示在短波长范围内。(3)反冲电子的动能将（2）-（1），可得\n3.X射线光子和原子内层电子相互作用光子质量远小于原子，碰撞时光子不损失能量，波长不变。原子λ0λ0内层电子被紧束缚，光子相当于和整个原子发生碰撞。光子内层电子外层电子波长变大的散射线波长不变的散射线(1)结论(2)波长0轻物质（多数电子处于弱束缚状态）弱强重物质（多数电子处于强束缚状态）强弱原子实=原子核+内层电子四.意义1.支持了“光量子”概念，首次证实了“光子具有动量”2.证实了在微观中动量和能量守恒定律成立\n例波长λ0=0.02nm的X射线与静止的自由电子碰撞，在与入射方向成90°角的方向上观察时。解(1)λ0λmv(1)散射X射线的波长多大？求(2)反冲电子的动能、动量各为多少？(2)反冲电子的动能、动量和速度各为多少？eV\n§16.4氢原子光谱玻尔的氢原子理论光谱:电磁辐射的波长成分和强度分布的记录1.实验装置记录氢原子光谱原理示意图氢放电管2~3kV狭缝全息干板三棱镜（或光栅）一.氢原子光谱\n2.光谱特征(1)分立线状光谱，每条谱线具有确定波长。1885年，巴耳末发现，氢原子在可见光区中谱线的波长可由一个简单的经验公式给出氢光谱的里德伯常量(2)巴耳末推测可存在别的氢光谱线系，它们可表示为k=1(n=2,3,4,…)谱线系——赖曼系（1906年）——巴耳末系k=3(n=4,5,6,…)谱线系——帕邢系（1908年）（3）进一步实验还发现所有元素的光谱都是线光谱，且都有其特征，是鉴别元素的极灵敏的方法，波长都可表示为\n3.经典理论解释氢原子的线状光谱遇到困难卢瑟福原子模型经典电磁理论解释：电子绕核运动辐射电磁波能量逐渐减小逐渐靠拢核原子不稳定旋转频率变化连续的光谱二.玻尔氢原子理论1.定态假设原子中的电子只能占有某些轨道，（1913年）每一个轨道具有确定的能量，不辐射电磁波。\n3.角动量量子化假设电子在定态时，轨道角动量为分立值2.跃迁假设：原子能量的任何变化（发射或吸收电磁辐射），仅在两个定态间以跃迁方式进行，电磁辐射频率为——Bohr频率公式r玻尔根据上述三条假设，应用经典力学和电磁学理论，建立了氢原子模型。\n电子绕核运动的向心力是库仑力由上两式得,第n个定态的轨道半径为r2=4r1r3=9r1电子能量-13.6eV玻尔半径波数(波长的倒数)当时实验测得其中计算得到\nEn(eV)氢原子能级图莱曼系巴耳末系帕邢系布拉开系-13.6-1.51-3.390光频n=1n=2n=3n=4n=5n=6\n里德伯-里兹并合原则(1896年)卢瑟福原子的有核模型（1911年）普朗克量子假设（1900年）玻尔氢原子理论(1913年）说明成功的把氢原子结构和光谱线结构联系起来。局限性:不能处理复杂原子的问题，根源在于对微观粒子的处理仍沿用了牛顿力学的观念玻尔的最伟大的贡献，就在于把量子化的原则推广到原子结构和电子运动的研究中，揭示了原子行为中存在的特殊的量子化原则，使量子论进入了原子物理学。\n例解双原子气体分子由质量为m的两个原子构成。这两个原子相隔一定的距离d并围绕其连线的中垂线旋转，假定它的角动量象玻尔氢原子理论中那样是量子化的，试确定其转动动能的可能值。mm角动量为角动量量子化有转动动能可能值为说明严格的量子理论给出分子转动动能为\n被重视被忽视光波波动性(λ,ν)粒子性(m,p)实物粒子粒子性(m,p)？16-5微观粒子的波粒二象性不确定关系一、德布罗意假设与物质波(MatterWave)1924年，法国物理学家德布罗意（deBroglie）提出假设:实物粒子具有波动性，实物的波粒二象性(wave-particledualism)与光子相类似德布罗意关系相对论效应情况下\n例一个棒球的质量m=1千克，速度v=10m/s求它的德布罗意波长解当今最精密的仪器也无法测出计算经过电势差U1=150V和U2=104V加速的电子的德布罗意波长（不考虑相对论效应）。例解根据，加速后电子的速度为根据德布罗意关系p=h/λ，电子的德布罗意波长为波长分别为可以通过晶体衍射证实电子的波动性\n例从德布罗意波导出氢原子波尔理论中角动量量子化条件.解两端固定的弦，若其长度等于波长则可形成稳定的驻波.将弦弯曲成圆时电子绕核运动其德布罗意波长为角动量量子化条件\n二、戴维孙（C.J.Davisson）和革末（L.H.Germer）实验1927年，实验观察到电子衍射，证实电子具有波性。电子枪晶体探测器电子束晶体戴维孙—革末电子散射实验（波长相同）X射线电子束布拉格公式德布罗意公式\n单缝双缝三缝四缝五缝1961年，约恩荪（C.Jonson）电子衍射实验，衍射图样为结论：波粒二象性是所有物质的普遍属性，是“遍及整个物质世界的一种绝对普遍的现象”。电子的单缝、双缝、三缝和四缝衍射实验（约恩逊1961）还验证了质子、中子和原子等实物粒子都具有波动性，并满足德布洛意关系。\n“forhisdiscoveryofthewavenatureofelectrons”TheNobelPrizeinPhysics1929deBroglie\n二.不确定关系(1927年,海森堡)1.动量—坐标不确定关系微观粒子的位置坐标x、动量分量px不能同时具有确定的值。一个量确定的越准确，另一个量的不确定程度就越大。分别是x、px的不确定量，其乘积说明(1)微观粒子的运动原则上没有轨道.(2)微观粒子不能静止.(3)若粒子的位置空间范围有限，且动量p>>p(104)，则粒子的位置和动量就是确定的，粒子可近似看作经典的质点.(4)不确定性关系是波粒二象性及其统计关系的直接结果.\npx电子束x电子经过狭缝，其坐标x的不确定量为△x；大部分电子落在中央明纹△x2.动量—坐标不确定关系说明\n动量分量px的不确定量为px0电子经过狭缝，其坐标x的不确定量为△x；电子束△xx减小缝宽△x,x确定的越准确px的不确定度,即△px越大\n子弹（m=0.10g,v=200m/s）穿过0.2cm宽的狭缝.例解求沿缝宽方向子弹的速度不确定量.子弹速度的不确定量为若让\n原子的线度约为10-10m，求原子中电子速度的不确定量。电子速度的不确定量为氢原子中电子速率约为106m/s。速率不确定量与速率本身的数量级基本相同，因此原子中电子的位置和速度不能同时完全确定，也没有确定的轨道。原子中电子的位置不确定量10-10m，由不确定关系例解说明\n例氦氖激光器所发红光波长=6328Å，谱线宽度=10-8Å.求当这种光子沿x方向传播时，它的x坐标不确定度(波列长度).解\n2.能量—时间不确定关系反映了原子能级宽度△E和原子在该能级的平均寿命△t之间的关系。基态辐射光谱线固有宽度激发态E基态寿命△t光辐射能级宽度平均寿命△t~10-8s平均寿命△t∞能级宽度△E0\n即与同数量级例解试证明粒子运动区域（或障碍物）的线度L与德布罗意波长之比和粒子动量p与其动量不确定量p之比具有相同的数量级设说明和具有相同的数量级，实际判别时只要分析其中的一个就可判别粒子是波动粒子还是经典粒子。如电视显象管中电子的速度v=105m/s，显象管尺寸L=0.1m，问此电子能否看作经典质点？此显象管中的电子可看作经典质点\n§16.6波函数一维定态薛定谔方程问题提出:粒子具有波性数学表述？光子波粒二象性一、概率波（probabilitywave）双缝衍射光子堆积曲线光子概念：光子概率：概率大概率小德国物理学家玻恩提出：“光波是一种概率波”。用概率描述光子分布玻恩假设：物质波是一种概率波，粒子在空间分布可通过概率确定和描述，其概率与图样强度相关。微观粒子堆积曲线\n“forhisfundamentalresearchinquantummechanics,especiallyforhisstatisticalinterpretationoftheWave-function”Bornandhiscolleaguesalsodevelopedthetheoryofcrystallatticevibrations,andthestatisticaltheoryoffluids.M.BornTheNobelPrizeinPhysics1954