大学物理--几何光学

大学物理--几何光学

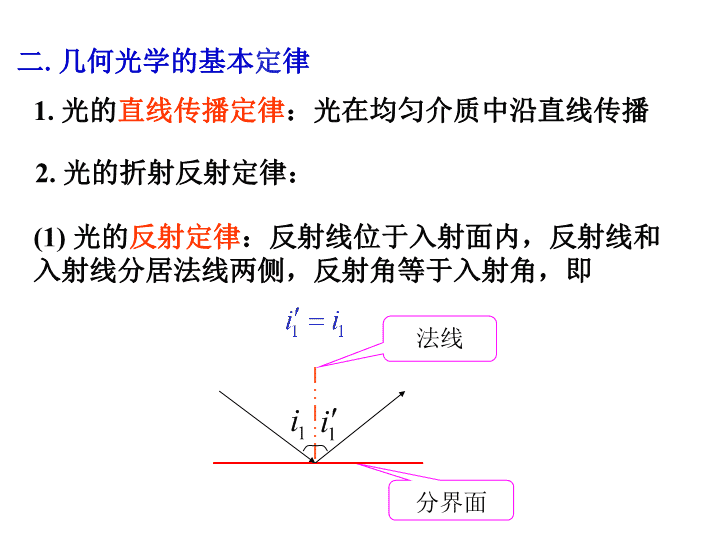
第章　几何光学几何光学是光学的一个重要分支，它以光的直线传播等实验规律为基础，用几何方法研究光在透明介质中的传播及光学仪器的成象等问题。本章主要内容有：几何光学的基本规律、费马原理、与成象有关的基本概念、近轴成象理论、眼睛及常用光学仪器的放大本领。\n§1几何光学的基本定律光线—光能传播方向的几何线光束—有一定几何关系的一些光线的集合一.光源和光线1.光源光源—任何发光物体：太阳、烛焰、钨丝白炽灯、日光灯、高压水银荧光灯等点光源—可看成几何上的点，只有空间位置无体积的光源2.光线和光束\n二.几何光学的基本定律1.光的直线传播定律：光在均匀介质中沿直线传播(1)光的反射定律：反射线位于入射面内，反射线和入射线分居法线两侧，反射角等于入射角，即2.光的折射反射定律：分界面法线\n(2)光的折射定律：折射线位于入射面内,折射线与入射线分居法线两侧，入射角的正弦与折射角的正弦之比为一与入射角无关的常数，即*漫射：当界面粗糙时,各入射点处法线不平行,即使入射光是平行的,反射光和折射光也向各方向分散开———漫反射或漫折射。介绍\n3.光的独立传播定律和光路可逆性原理光在传播过程中与其他光束相遇时，各光束都各自独立传播，不改变其传播方向。光沿反方向传播时，必定沿原光路返回。即在几何光学中，任何光路都是可逆的。三、几何光学定律成立的条件（1）必须是均匀介质，即同一介质的折射率处处相等，折射率不是位置的函数。（2）必须是各向同性介质，即光在介质中传播时各个方向的折射率相等，折射率不是方向的函数。\n（3）光强不能太强，否则巨大的光能量会使线性叠加原理不再成立而出现非线性情况。（4）光学元件的线度应比光的波长大得多，否则不能把光束简化为光线。§2费马原理费马原理是一个描述光线传播行为的原理.一.光程在均匀介质中,光程为光在介质中通过的几何路程l与该介质的折射率n的乘积：\n光程表示光在介质中通过真实路程所需时间内,在真空中所能传播的路程。直接用真空中的光速来计算光在不同介质中通过一定几何路程所需要的时间。分区均匀介质:连续介质:\n二、费马原理1.表述：光在空间两定点间传播时，实际光程为一特定的极值。2.表达式：nBAdl3.说明：意义：费马原理是几何光学的基本原理，用以描述光在空间两定点间的传播规律。极值的含义：极小值，极大值，恒定值。一般情况下，实际光程大多取极小值。\n三.由费马原理导出几何光学定律在均匀介质中折射率为常数1.直线传播定律：所以光在均匀介质中沿直线传播而由公理：两点间直线距离最短的极小值为直线ABAB\n2.光的反射定律P’是P点关于Σ面的对称点。P，Q，O三点确定平面Π。直线QP’与反射面Σ交于O点。则易知当i’=i时，QO+OP为光程最短的路径。Q点发出的光经反射面Σ到达P点\n3.光的折射定律：i2n2B‘C‘’A’C‘CBAn1O’OPMi1XYZＡ点发出的光线入射到两种介质的平面分界面上，折射后到达Ｂ点。①折射线在入射线和法线决定的平面内如图：只需证明折射点C点在交线OO’上即可.反证法：设有另一点C’位于OO’线外，则在OO’上必可找到其垂足C’’，\n即光程ΔAC’B>ΔAC’’B这与费马原理矛盾!所以折射点在交线上，折射线在入射线和法线所决定的平面内②折射线、入射线分居法线两侧A、B、C点坐标如图，沿此方向入射必有ACB光程为：i2n2B‘A’CBAn1O’OPMi1XYZ\ni2n2B‘A’CBAn1O’OPMi1XYZ光程取极值，光程对x求一阶导数,令其为0由三角形几何关系可得此即折射定律\n回转抛物面焦点发出的光，反射后变为平行光，会聚在无穷远处，光程为极大值。AB\n回转椭球面内两焦点间光的路径，光程为恒定值。AB\n在回转椭球面上一点作相切的平面和球面，则经平面反射的光线中，实际光线光程最小；经球面反射的光线中，实际光线光程最大。AB\n4.物像之间的等光程性可以证明：在物点Q与像点Q’之间，不管光线经何路径，凡是由Q通过同样的光学系统到达Q’的光线，都是等光程的。QQ’\n§3.单心光束实像和虚像一.单心光束、实像、虚像1.发光点：只有几何位置而没有大小的发射光束的光源。若光线实际发自于某点，则称该点为实发光点；若某点为诸光线反向延长线的交点，则该点称为虚发光点。2.单心光束：只有一个交点的光束，称单心光束。此交点也称为光束的顶点。\n发散单心光束会聚单心光束3.实像、虚像当顶点为光束的发出点时，该顶点称为光源、物点。当单心光束经光学系统折射或反射后，仍能找到一个顶点，称光束保持了其单心性。该顶点称为象点。\n实象：有实际光线会聚的象点。虚象：无实际光线会聚的象点。（光束反向延长线的交点）。P‘PP’P实像虚像光学系统光学系统\n光学系统实物成虚实象光学系统物空间像空间实物成实象光学系统虚物成实象二、物空间与像空间\n§4光在平面介面上的反射和折射一般情况下，光在介面上反射和折射后，其单心性不再保持。但只要满足适当的条件，可以近似地得到保持。接下来的两节，主要研究在不同介面反射、折射时，光束单心性的保持情况。一、光在平面上的反射DM’MP‘PCBA点光源P发出单心光束，经平面镜反射后，形成一束发散光束，其反向延长线交于一点P‘，且与P点对称。平面镜是一个不破坏光束单心性、理想成像的完善的光学系统。并且也是唯一的一个。\n二、光在平面介面上的折射光束单心性的破坏介质n1中的发光点P发出单心光束经介面XOZ折射后进入介质n2，现取其中一微元光束，在XOY平面内,其折射光束的反向延长线交于P’点，并与OY轴交于P1、P2两点。折射后，光束的单心性已被破坏!xB1B2n2n1OyP2P1PP`i1i2i1+△i1i2＋△i2A1A2●●z×\n三.全反射光学纤维全反射：全反射的条件：只有反射而无折射的现象称为全反射。应用：光学纤维xA3n2n1OyPi1i2icA1A2\n四.棱镜EDCB1.偏向角、最小偏向角：棱镜是一种由多个平面界面组合而成的光学元件。光通过棱镜时，产生两个或两个以上界面的连续折射，传播方向发生偏折。最常用的棱镜是三棱镜。三棱镜两折射面的夹角称三棱镜顶角A。An2n1出射光与入射光之间的夹角称棱镜的偏向角。\nEDCBAn2n1此时，入射角最小偏向角：可以证明：当光路对称+2sin2sinsinsin0212AAiin==q:,1n1=则由折射定律有即若此时三棱镜处于空气中θ达最小值即：\n分光：当用白光入射时，由于折射率的不同，出射光将展开成彩带即光谱。改变光路：如右图示4504502.应用\n§5光在单球面上的近轴成象一.基本概念和符号规则光轴：若光学系统由球面组成，各球心的连线在一条直线上，则称为共轴球面系统，这条直线为该光学系统的光轴。nn´rdhQODCQ´P´-PM光轴顶点\n（1）线段：光轴方向上，以顶点为起点，沿光线进行方向为正，反之为负；垂直方向上，主光轴上方为正，反之为负。（2）球面的曲率半径：球心在球面顶点的右方为正，反之为负。(自左向右为正方向）符号规则：nn´rdhQODCQ´P´-PM★\n（3）物距：自参考点（球面顶点、薄透镜的光心）到物点，沿光线方向为正，反之为负。（4）象距：自参考点（球面顶点、薄透镜的光心）到象点，沿光线方向为正，反之为负。（5）物高和象高：物高和象高垂直于光轴，向上为正，反之为负。（6）角度：以光轴或界面法线为始边，旋转到该光线，旋转方向为顺时针，角度为正，反之为负。此外，还规定在图上只标记角度和线段的绝对值，若某一字母表示负的数值，则在其前面标以负号。★★\nyQ二、球面反射对单心性的破坏PACOP`-s`-r-s-ui-i`-u`从主轴上P点发出单心光束，其中一条光线在球面上A点反射，反射光与主轴交于P’点。即P’为P的像。()()()()()()()()jjcos2cos2'2'2'22rsrrsrlsrrsrrl----+-=--+-+-=在ΔPAC和ΔP’AC中由余弦定理有：\nPACOP`-s`-r-s-ui-i`-u`对给定的物点，不同的入射点，对应着不同的入射线和反射线，对应着不同的。()()()()()()()()jjcos2cos2'2'222''rsrrsrnsrrsrrnnlnlPAP----+-+--+-+-=+=D光程：\n对一定的球面和发光点P（S一定），不同的入射点对应有不同的S‘。即：同一个物点所发出的不同光线经球面反射后不再交于一点。由P点所发出的单心光束经球面反射后，单心性被破坏。\n三、近轴光线下球面反射的物像公式1.近轴光线条件即：对一定的反射球面，Ｓ‘和Ｓ一一对应，而与入射点无关。\n∴由P点所发出的单心光束，经球面反射后将交于一点P‘，光束的单心性得以保持。一个物点将有一个确定像点与之对应。光学上称：很小的区域为近轴（或傍轴）区域，此区域内的光线为近轴光线。∴近轴条件下球面反射不破坏光束的单心性。2.物像公式有当ACOP`-s`-r-sF`焦点：沿主轴方向的平行光束经球面反射后将会聚于主轴上一点，该点称为反射球面的焦点(F’)。2r\nACOP`-s`-r-sF`焦距：焦点到球面顶点的距离（）。说明：1、它是球面反射成像的基本公式，只在近轴条件下成立；2、式中各量必须严格遵从符号法则；3、对凸球面反射同样适用；4、当光线从右至左时同样适用。球面反射的物象公式\n四.球面折射对光束单心性的破坏Pn-u-i1A-i2n`u`CP`Or-ss`设n

查看更多