大学物理讲义(下)

大学物理讲义(下)

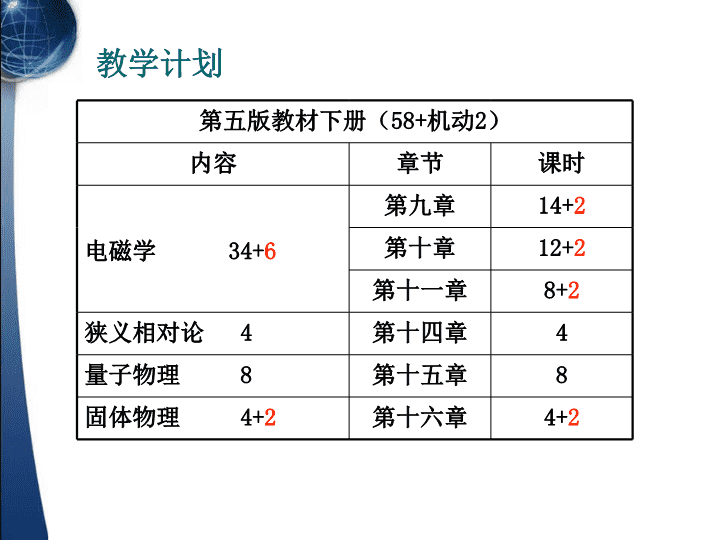
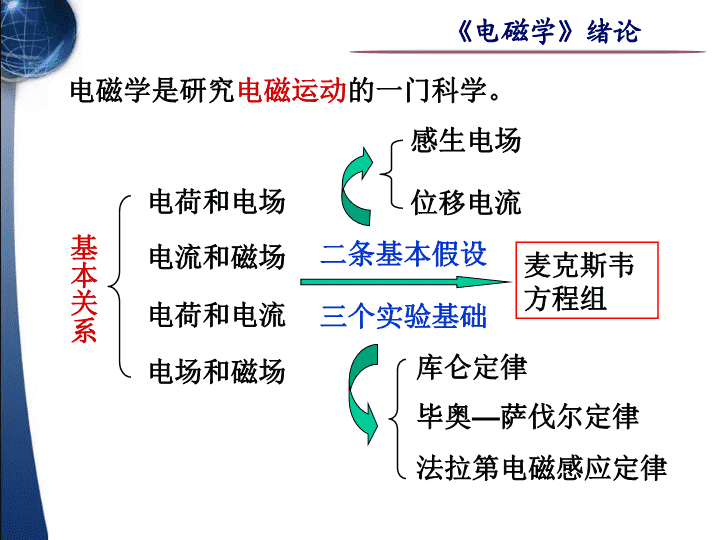
大学物理A(下)主讲教师程庆华开课单位物理科学与技术学院\n第五版教材下册（58+机动2）内容章节课时电磁学34+6第九章14+2第十章12+2第十一章8+2狭义相对论4第十四章4量子物理8第十五章8固体物理4+2第十六章4+2教学计划\n《电磁学》绪论电磁学是研究电磁运动的一门科学。电荷和电场基本关系电流和磁场电荷和电流电场和磁场二条基本假设三个实验基础麦克斯韦方程组库仑定律毕奥—萨伐尔定律法拉第电磁感应定律感生电场位移电流\n第9章静电场图为1930年E.O.劳伦斯制成的世界上第一台回旋加速器\n9-0教学基本要求一掌握描述静电场的两个基本物理量——电场强度和电势的概念，理解电场强度是矢量点函数，而电势V则是标量点函数.二理解静电场的两条基本定理——高斯定理和环路定理，明确认识静电场是有源场和保守场.三掌握用点电荷的电场强度和叠加原理以及高斯定理求解带电系统电场强度的方法.\n9-0教学基本要求四掌握静电平衡的条件，掌握导体处于静电平衡时的电荷、电势、电场分布.五理解电场能量密度的概念，掌握电场能量的计算.六了解电介质的极化机理，掌握电位移矢量和电场强度的关系.理解电介质中的高斯定理，并会用它来计算电介质中对称电场的电场强度.\n一.电荷1.正负性2.量子性盖尔—曼提出夸克模型:3.守恒性在一个孤立系统中总电荷量是不变的。即在任何时刻系统中的正电荷与负电荷的代数和保持不变，这称为电荷守恒定律。4.相对论不变性电荷的电量与它的运动状态无关9.1电荷库仑定律\n二.库仑定律1.点电荷(一种理想模型)当带电体的大小、形状与带电体间的距离相比可以忽略时,就可把带电体视为一个带电的几何点。2.库仑定律处在静止状态的两个点电荷，在真空（空气）中的相互作用力的大小，与每个点电荷的电量成正比，与两个点电荷间距离的平方成反比，作用力的方向沿着两个点电荷的连线。电荷q1对q2的作用力F219.1电荷库仑定律\n电荷q2对q1的作用力F12真空中的电容率（介电常数）讨论：(1)库仑定律适用于真空中的点电荷；(2)库仑力满足牛顿第三定律；(3)一般9.1电荷库仑定律\n三.电场力的叠加q3受的力：对n个点电荷：对电荷连续分布的带电体Qr9.1电荷库仑定律\n已知两杆电荷线密度为，长度为L，相距L解例两带电直杆间的电场力。求L3L2LxO\n一.静电场后来:法拉第提出场的概念早期：电磁理论是超距作用理论电场的特点(1)对位于其中的带电体有力的作用(2)带电体在电场中运动,电场力要作功二.电场强度检验电荷带电量足够小点电荷场源电荷产生电场的电荷==在电场中任一位置处：9.2静电场电场强度\n电场中某点的电场强度的大小等于单位电荷在该点受力的大小，其方向为正电荷在该点受力的方向。三.电场强度叠加原理点电荷的电场定义：点电荷系的电场点电荷系在某点P产生的电场强度等于各点电荷单独在该点产生的电场强度的矢量和。这称为电场强度叠加原理。\n连续分布带电体:线密度:面密度:体密度P\n求电偶极子在延长线上和中垂线上一点产生的电场强度。解例OxP令：电偶极矩Pr在中垂线上\nPxyO它在空间一点P产生的电场强度（P点到杆的垂直距离为a)解dqr由图上的几何关系21例长为L的均匀带电直杆，电荷线密度为求a\n(1)a>>L杆可以看成点电荷讨论(2)无限长直导线PxyOdqr21a\n圆环轴线上任一点P的电场强度RP解dqOxr例半径为R的均匀带电细圆环，带电量为q求圆环上电荷分布关于x轴对称\n(1)当x=0（即P点在圆环中心处）时，(2)当x>>R时可以把带电圆环视为一个点电荷讨论RPdqOxr\n面密度为的圆板在轴线上任一点的电场强度解PrxO例R\n(1)当R>>x，圆板可视为无限大薄板(2)E1E1E1E2E2E2(3)补偿法pxO讨论\nOx圆环对杆的作用力qL解R例已知圆环带电量为q，杆的线密度为，长为L求圆环在dq处产生的电场\n例解相对于O点的力矩(1)力偶矩最大力偶矩为零(电偶极子处于稳定平衡)(2)(3)力偶矩为零(电偶极子处于非稳定平衡)求电偶极子在均匀电场中受到的力偶矩。讨论O\n场强方向沿电力线切线方向，场强大小决定电力线的疏密。电场线是非闭合曲线，不相交。起始于正电荷(或无穷远处)，终止于负电荷(或无穷远处)。dN一.电场线（电力线）9.3电通量高斯定理\n二.电通量在电场中穿过任意曲面S的电场线条数称为穿过该面的电通量。1.均匀场中定义2.非均匀场中dSEn\n非闭合曲面凸为正，凹为负闭合曲面向外为正，向内为负(2)电通量是代数量为正为负对闭合曲面方向的规定：(1)讨论\n三.高斯定理取任意闭合曲面时以点电荷为例建立e——q关系:结论:e与曲面的形状及q在曲面内的位置无关。取球对称闭合曲面-q+q+q\nS+qS1S2q在曲面外时：当存在多个电荷时：q1q2q3q4q5是所有电荷产生的，e只与内部电荷有关。结论:\n（不连续分布的源电荷）（连续分布的源电荷）反映静电场的性质——有源场真空中的任何静电场中，穿过任一闭合曲面的电通量，在数值上等于该曲面内包围的电量的代数和乘以高斯定理意义四.用高斯定理求特殊带电体的电场强度\n均匀带电球面，总电量为Q，半径为R电场强度分布QR解取过场点P的同心球面为高斯面P对球面外一点P:r根据高斯定理++++++例求\nrEOR++++++对球面内一点:E=0电场分布曲线\n例已知球体半径为R，带电量为q（电荷体密度为）R++++解球外r均匀带电球体的电场强度分布求球内()r'电场分布曲线REOr\n解电场强度分布具有面对称性选取一个圆柱形高斯面已知“无限大”均匀带电平面上电荷面密度为电场强度分布求例根据高斯定理有xOEx\n例已知无限大板电荷体密度为，厚度为d板外：板内：解选取如图的圆柱面为高斯面求电场场强分布dSSdxxOEx\n已知“无限长”均匀带电直线的电荷线密度为+解电场分布具有轴对称性过P点作一个以带电直线为轴，以l为高的圆柱形闭合曲面S作为高斯面例距直线r处一点P的电场强度求根据高斯定理得rlP\n电场分布曲线总结用高斯定理求电场强度的步骤：(1)分析电荷对称性；(2)根据对称性取高斯面；高斯面必须是闭合曲面高斯面必须通过所求的点EOr(3)根据高斯定理求电场强度。高斯面的选取使通过该面的电通量易于计算\n一.静电力作功的特点•单个点电荷产生的电场中baLq0(与路径无关)O9.4静电场的环路定理电势能\n结论电场力作功只与始末位置有关，与路径无关，所以静电力是保守力，静电场是保守力场。•任意带电体系产生的电场中电荷系q1、q2、…的电场中，移动q0，有abL••\n在静电场中，沿闭合路径移动q0，电场力作功L1L2二.静电场的环路定理环路定理ab\n静电场是无旋场的旋度(1)环路定理是静电场的另一重要定理，可用环路定理检验一个电场是不是静电场。不是静电场abcd讨论\n(2)环路定理要求电力线不能闭合。(3)静电场是有源、无旋场，可引进电势能。三.电势能•电势能的差力学保守力场引入势能静电场保守场引入静电势能定义：q0在电场中a、b两点电势能之差等于把q0自a点移至b点过程中电场力所作的功。\n•电势能取势能零点W“0”=0q0在电场中某点a的电势能：(1)电势能应属于q0和产生电场的源电荷系统共有。说明(3)选势能零点原则：(2)电荷在某点电势能的值与零点选取有关,而两点的差值与零点选取无关•实际应用中取大地、仪器外壳等为势能零点。•当(源)电荷分布在有限范围内时，势能零点一般选在　无穷远处。•无限大带电体，势能零点一般选在有限远处一点。\n如图所示,在带电量为Q的点电荷所产生的静电场中，有一带电量为q的点电荷解选无穷远为电势能零点bacQq在a点和b点的电势能求例选C点为电势能零点两点的电势能差：\n•电势差一.电势电势差单位正电荷自ab过程中电场力作的功。•电势定义单位正电荷自该点“势能零点”过程中电场力作的功。arq•点电荷的电势9.5电势电势差\n二.电势叠加原理•点电荷系的电势P对n个点电荷\n在点电荷系产生的电场中，某点的电势是各个点电荷单独存在时，在该点产生的电势的代数和。这称为电势叠加原理。对连续分布的带电体三.电势的计算方法（1）已知电荷分布（2）已知场强分布\n均匀带电圆环半径为R，电荷线密度为。解建立如图坐标系，选取电荷元dq例圆环轴线上一点的电势求RPOxdqr\n半径为R，带电量为q的均匀带电球体解根据高斯定律可得：求带电球体的电势分布例++++++RrP对球外一点P对球内一点P1P1\n例真空中有一电荷为Q，半径为R的均匀带电球面.试求（1）球面外两点间的电势差；（2）球面内两点间的电势差；（3）球面外任意点的电势；（4）球面内任意点的电势.\n解（1）（2）\n（3）令（4）\n一.等势面电场中电势相等的点连成的面称为等势面。点电荷电偶极子电场线等势面电场线等势面9.6等势面\n带电平板电容器内部示波管内部的电场电场线等势面电场线等势面\n1.等势面的性质(1)电场线与等势面处处正交。ab沿等势面移动电荷时，电场力所作的功为零。(2)规定相邻两等势面间的电势差都相同等势面密大等势面疏小(3)电场强度的方向总是指向电势降落的方向。\n2.电势与电场强度的微分关系取两相邻的等势面uabu+du把点电荷q0从a移到b，电场力作功为任意一场点处电场强度的大小等于沿过该点等势面法线方向上电势的变化率，负号表示电场强度的方向指向电势减小的方向。\n在直角坐标系中另一种理解：电势沿等势面法线方向的变化率最大电场强度在l方向的投影等于电势沿该方向变化率的负值某点的电场强度等于该点电势梯度的负值\n例求(2，3，0)点的电场强度。已知解\n一.导体的静电平衡9.7静电场中的导体金属导体的微观结构体心立方晶格单元金属导体在电结构方面的重要特征是：具有大量的自由电子导体不带电或不受外电场影响时，自由电子仅有微观热运动。金属性结合示意图+++++\n一.导体的静电平衡在外电场的作用下，导体中出现电荷重新分布。++++++图3+++图2图1设外电场为静电感应\n一.导体的静电平衡1.静电平衡导体内部和表面上任何一部分都没有宏观电荷运动，我们就说导体处于静电平衡状态2.导体静电平衡的条件导体表面3.静电平衡导体的电势导体静电平衡时，导体上各点电势相等，即导体是等势体，表面是等势面\n由导体的静电平衡条件和静电场的基本性质，可以得出导体上的电荷分布(有外场而且导体带电)1.静电平衡导体的内部处处不带电证明：在导体内任取体积元由高斯定理体积元任取导体带电只能在表面！二.导体上电荷的分布导体中各处如果,有空腔,且空腔中无电荷,则如果,有空腔,且空腔中有电荷,则电荷只能分布在外表面！在内外表面都分布有电荷分布！+q---------------\n2.静电平衡导体表面附近的电场强度与导体表面电荷的关系设导体表面电荷面密度为设P是导体外紧靠导体表面的一点,相应的电场强度为为导体外法线方向确定电场强度E和电荷密度的关系:++++ds注意：上式中的电场是合场强。++++\n+++++++++++++++++++尖端放电导体球孤立带电由实验可得以下定性的结论：ABC3.处于静电平衡的孤立带电导体电荷分布（危害、应用）金属尖端绝缘支架金属支架绝缘座\n腔内、腔外的场互不影响。4.静电屏蔽\n如图所示,导体球附近有一点电荷q。解接地即由导体是个等势体O点的电势为0则接地后导体上感应电荷的电量设感应电量为Q0？例求\n两球半径分别为R1、R2，带电量q1、q2，设两球相距很远，当用导线将彼此连接时，电荷将如何分布？解设用导线连接后，两球带电量为R2R1例\n已知导体球壳A带电量为Q，导体球B带电量为q(1)将A接地后再断开，电荷和电势的分布；解A与地断开后,ArR1R2B-q电荷守恒(2)再将B接地，电荷和电势的分布。A接地时，内表面电荷为-q外表面电荷设为设B上的电量为根据孤立导体电荷守恒例求(1)(2)\nB球圆心处的电势总结(有导体存在时静电场的计算方法)1.静电平衡的条件和性质:2.电荷守恒定律3.确定电荷分布,然后求解ArR1R2B-q\n例两块等面积的金属平板，分别带电荷qA和qB，平板面积均为S，两板间距为d，且满足面积的线度远大于d。静电平衡时两金属板各表面上的电荷面密度。求解如图示，设4个表面的电荷面密度分别为q1、q2、q3和q4，dSSqAqB1234由电荷守恒，得在两板内分别取任意两点A和B，则AB①\n代入①，得可见，A、B两板的内侧面带等量异号电荷；两板的外侧面带等量同号电荷。特别地，若qA＝－qB＝q，则电荷只分布在两板的内侧面，外侧面不带电。dSSqAqB1234AB\n电容只与导体的几何因素和介质有关，与导体是否带电无关三.孤立导体的电容单位:法拉(F)孤立导体的电势孤立导体的电容++++++++++++++++Qu↑E↑求半径为R的孤立导体球的电容.电势为电容为R\n若R=Re,则C=714F若C=110–3F,则R=?C=110-3F啊,体积还这么大!1.8m9m通常，由彼此绝缘相距很近的两导体构成电容器。极板极板+Q-Qu使两导体极板带电两导体极板的电势差电容器的电容四.电容器的电容\n电容器电容的计算Q电容器电容的大小取决于极板的形状、大小、相对位置以及极板间介质。duS+Q-Q(1)平行板电容器\n(2)球形电容器R1+Q-QR2ab(3)柱形电容器R1R2l\n若R1>>R2-R1,则C=?讨论uR1R2l\n电容器的应用：储能、振荡、滤波、移相、旁路、耦合等。电容器的分类形状：平行板、柱形、球形电容器等介质：空气、陶瓷、涤纶、云母、电解电容器等用途：储能、振荡、滤波、移相、旁路、耦合电容器等。\n2.5厘米高压电容器(20kV5~21F)(提高功率因数)聚丙烯电容器(单相电机起动和连续运转)陶瓷电容器(20000V1000pF)涤纶电容(250V0.47F)电解电容器(160V470F)12厘米2.5厘米70厘米\nAB以平行板电容器为例，来计算电场能量。+设在时间t内，从B板向A板迁移了电荷在将dq从B板迁移到A板需作功极板上电量从0—Q作的总功为9.8电场能量\n忽略边缘效应，对平行板电容器有能量密度不均匀电场中（适用于所有电场）\n已知均匀带电的球体，半径为R，带电量为QRQ从球心到无穷远处的电场能量解r求例取体积元\n一.充满电介质的电容器电介质:绝缘体(放在电场中的)电介质电场r实验r—电介质的相对介电常数结论:介质充满电场或介质表面为等势面时+Q-Q++++++++++++++++----------------介质中电场减弱9.9静电场中的电介质\n二.电介质的极化极化电荷无极分子有极分子+-无外场时（热运动）整体对外不显电性(无极分子电介质)(有极分子电介质)\n-------+++++++有外场时(分子)位移极化(分子)取向极化束缚电荷´束缚电荷´无极分子电介质有极分子电介质´\n三.电介质内的电场强度r+++++++++---------+++++++++++++++++--------------------\n四.电介质的高斯定理电位移矢量无电介质时加入电介质r+++++++++---------+++++++++++++++++--------------------—介电常数令：\n通过高斯面的电位移通量等于高斯面所包围的自由电荷的代数和，与极化电荷及高斯面外电荷无关。比较介质中的电场能量密度\n例平行板电容器，其中充有两种均匀电介质。求(1)各电介质层中的场强(2)极板间电势差解做一个圆柱形高斯面同理，做一个圆柱形高斯面\n•各电介质层中的场强不同•相当于电容器的串联\n平板电容器中充介质的另一种情况由极板内为等势体考虑到•各电介质层中的场强相同•相当于电容器的并联