- 2022-08-16 发布 |
- 37.5 KB |
- 10页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
大学物理考前习题
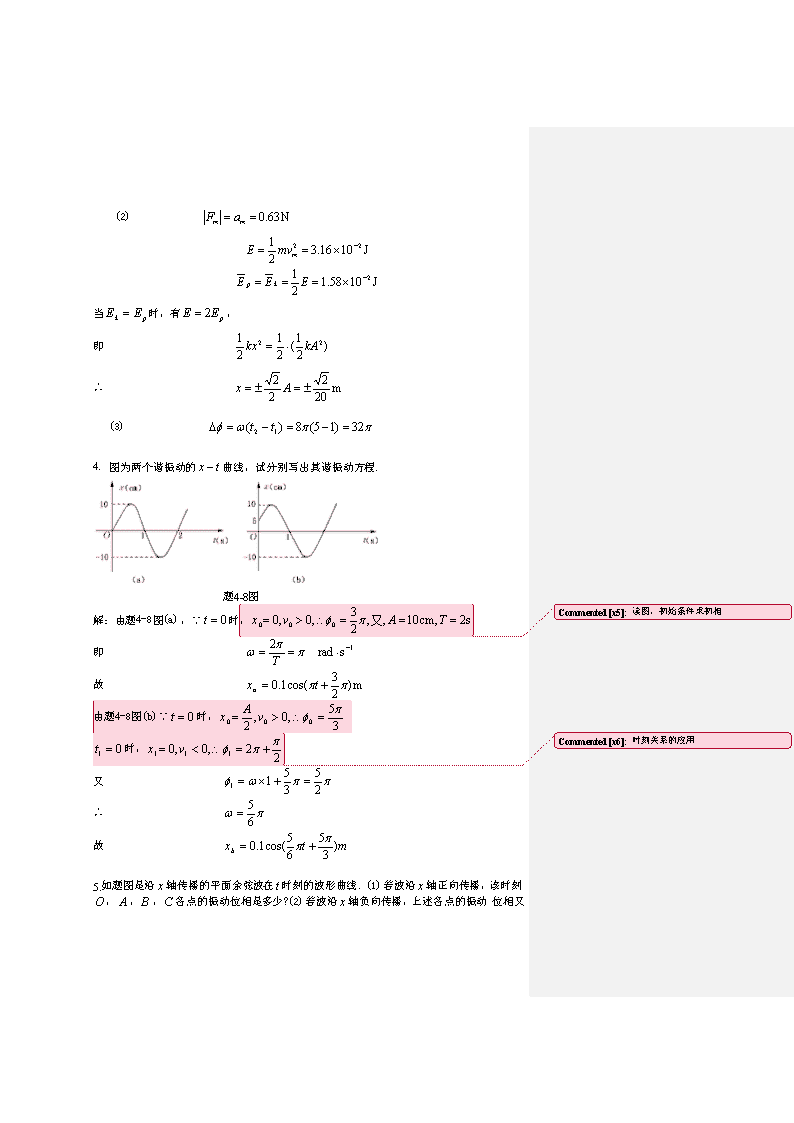
注:这些没有一个考试题目,但只要你会了,考试就不会有任何,但如果你只是背了,呵呵,不知道结果了。1如题4-3图所示,物体的质量为,放在光滑斜面上,斜面与水平面的夹角为,弹簧的倔强系数为,滑轮的转动惯量为,半径为.先把物体托住,使弹簧维持原长,然后由静止释放,试证明物体作简谐振动,并求振动周期.题4-3图解:分别以物体和滑轮为对象,其受力如题4-3图(b)所示,以重物在斜面上静平衡时位置为坐标原点,沿斜面向下为轴正向,则当重物偏离原点的坐标为时,有①②③这类题目,力学分析的应用,包括牛顿定律和转动定律。式中,为静平衡时弹簧之伸长量,联立以上三式,有平衡位置的确定令则有故知该系统是作简谐振动,其振动周期为2.一质量为M的盘子系于竖直悬挂的轻弹簧下端,弹簧的劲度系数为k。现有一质量为m的物体自离盘h\n高处自由下落,掉在盘上没有反弹,以物体掉在盘上的瞬时作为计时起点,求盘子的振动表式。(取物体掉入盘子后的平衡位置为坐标原点,位移以向下为正。)解:与M碰撞前,物体m的速度为由动量守恒定律,碰撞后的速度为碰撞点离开平衡位置距离为碰撞后,物体系统作简谐振动,振动角频率为由简谐振动的初始条件,得初始条件求初相:∴振动表达式为:3.质量为的小球与轻弹簧组成的系统,按的规律作谐振动,求:(1)振动的周期、振幅和初位相及速度与加速度的最大值;(2)最大的回复力、振动能量、平均动能和平均势能,在哪些位置上动能与势能相等?(3)与两个时刻的位相差;解:(1)设谐振动的标准方程为,则知:又谐振动中的关键量都与振幅、频率、相位有关。\n(2)当时,有,即∴(3)4.图为两个谐振动的曲线,试分别写出其谐振动方程.题4-8图解:由题4-8图(a),∵时,读图,初始条件求初相即故由题4-8图(b)∵时,时,时刻关系的应用又∴故5.如题图是沿轴传播的平面余弦波在时刻的波形曲线.(1)若波沿轴正向传播,该时刻,,,各点的振动位相是多少?(2)若波沿轴负向传播,上述各点的振动\n位相又是多少?解:(1)波沿轴正向传播,则在时刻,有对于点:∵,∴对于点:∵,∴对于点:∵,∴对于点:∵,∴(取负值:表示点位相,应落后于点的位相)(2)波沿轴负向传播,则在时刻,有对于点:∵,∴对于点:∵,∴对于点:∵,∴对于点:∵,∴(此处取正值表示点位相超前于点的位相)波形图的理解6.一列机械波沿轴正向传播,=0时的波形如题5-13图所示,已知波速为10m·s-1,波长为2m,求:(1)波动方程;(2)点的振动方程及振动曲线;(3)点的坐标;(4)点回到平衡位置所需的最短时间.解:由题5-13图可知,时,,∴,由题知,,则∴波速、波长、频率(1)波动方程为\n题5-13图(2)由图知,时,,∴(点的位相应落后于点,故取负值)∴点振动方程为(3)∵∴解得(4)根据(2)的结果可作出旋转矢量图如题5-13图(a),则由点回到平衡位置应经历的位相角题5-13图(a)∴所属最短时间为7.已知平面简谐波的波动方程为(SI).(1)写出=4.2s时各波峰位置的坐标式,并求此时离原点最近一个波峰的位置,该波峰何时通过原点?(2)画出=4.2s时的波形曲线.解:(1)波峰位置坐标应满足解得(…)所以离原点最近的波峰位置为.∵故知,∴,这就是说该波峰在波动方程的意义。前通过原点,那么从计时时刻算起,则应是,即该波峰是在时通过原点的. \n题5-15图(2)∵,∴,又处,时,又,当时,,则应有解得,故时的波形图如题5-15图所示8.如题5-12图所示,已知=0时和=0.5s时的波形曲线分别为图中曲线(a)和(b),波沿轴正向传播,试根据图中绘出的条件求:(1)波动方程;(2)点的振动方程.解:(1)由题5-12图可知,,,又,时,,∴,而,,∴读图故波动方程为(2)将代入上式,即得点振动方程为9.在杨氏双缝实验中,双缝间距=0.20mm,缝屏间距=1.0m,试求:(1)若第二级明条纹离屏中心的距离为6.0mm,计算此单色光的波长;(2)相邻两明条纹间的距离.解:(1)由知,,(2)双绛方程,隐含光程差。\n10.波长400nm到750nm的白光垂直照射到某光栅上,在离光栅0.50m处的光屏上测得第一级彩带离中央明条纹中心最近的距离为4.0cm,求:(1)第一级彩带的宽度;(2)第三级的哪些波长的光与第二级光谱的光相重合。解:(1)衍射光栅中波长越小,则离中央明纹就越近,所以:那么750nm的波长的第一级条纹位置在:第一级彩带的宽度:(2)第二级的750nm的波长对应的光的位置:第三级中有一部分和它将重合:对应的波长为400——500nm的波分光,11.用的单色光垂直照射在宽为,共有5000条缝的光栅上。问:(1)光栅常数是多少?(2)第二级主极大的衍射角为多少?(3)光屏上可以看到的条纹的最大级数?解:(1)由光栅衍射明纹公式(2),(3),因为10级是看不到的(没有衍射能量),所以最大级数为9。光栅方程的应用12.一个平面透射光栅,当用光垂直入射时,能在30度角的衍射方向上得到600nm的第二级主极大,但不能得到400nm的第三级主极大,求:(1)此光栅的透光部分的宽度a和不透光部分的宽度b;解:(1)利用:根据题意:30度角的衍射方向上得到600nm的第二级主极大,所以:不能得到400nm的第三级主极大:说明第三级条纹缺级。由缺级的定义可得到:缺级关系所以:a=800nm,b=1600nm。\n13.1mol单原子理想气体从300K加热到350K,问在下列两过程中吸收了多少热量?增加了多少内能?对外作了多少功?(1)体积保持不变;(2)压力保持不变.解:(1)等体过程由热力学第一定律得吸热对外作功(2)等压过程吸热内能增加对外作功热力学第一定律的在等值过程中的应用。14.一卡诺热机在1000K和300K的两热源之间工作,试计算(1)热机效率;(2)若低温热源不变,要使热机效率提高到80%,则高温热源温度需提高多少?(3)若高温热源不变,要使热机效率提高到80%,则低温热源温度需降低多少?解:(1)卡诺热机效率 (2)低温热源温度不变时,若要求K,高温热源温度需提高(3)高温热源温度不变时,若\n要求K,低温热源温度需降低卡诺热机的特点15.设有个粒子的系统,其速率分布如题6-18图所示.求(1)分布函数的表达式;(2)与之间的关系;(3)速度在1.5到2.0之间的粒子数.(4)粒子的平均速率.(5)0.5到1区间内粒子平均速率.题6-18图解:(1)从图上可得分布函数表达式满足归一化条件,但这里纵坐标是而不是故曲线下的总面积为,(2)由归一化条件可得(3)可通过面积计算(4)个粒子平均速率(5)到区间内粒子平均速率分布率的概念\n查看更多