大学物理期末复习

大学物理期末复习

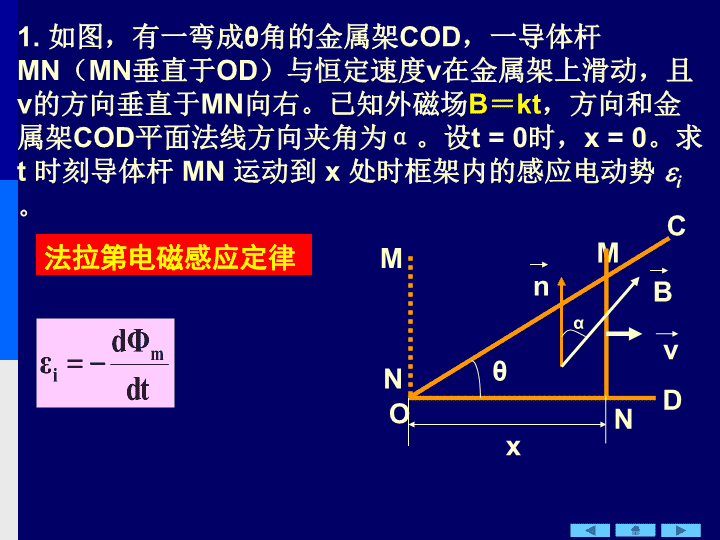
电磁感应感应电动势动生电动势感生电动势自感系数长直密绕螺线管磁场能量磁能密度麦氏方程组\n1.如图，有一弯成θ角的金属架COD，一导体杆MN（MN垂直于OD）与恒定速度v在金属架上滑动，且v的方向垂直于MN向右。已知外磁场B＝kt，方向和金属架COD平面法线方向夹角为α。设t=0时，x=0。求t时刻导体杆MN运动到x处时框架内的感应电动势i。MθNOxvCDMNBnα法拉第电磁感应定律\n法拉第电磁感应定律类似题目：习题集(第7章)（一）1；（四）2M→N顺时针\n1.B常量、v变速2.B不均匀、v匀速两个特例\n2.如图所示,长度为l的直导线ab在均匀磁场B中以速度v运动，直导线ab中的电动势为（A）Blv，（B）Blvsin,（C）Blvcos,（D）0。abl\nBOa3.半圆弧Oa在均匀磁场B中以匀角速度绕O点转动，求Oa两端的电动势（Oa=d）。解：作辅助线，连接Oa，构成闭合回路=0=0方向：a→OVO>VaaO\n4.如图，长直导线中通有电流I，有一四分之一圆弧AB构成的扇形平面在通电导线的平面内，以恒定的速度沿与通电导线平行的方向移动。圆心O点到导线的垂直距离为a。求：任意时刻AB弧中的动生电动势，并指出A、B那端的电势高。ABOvaLI建如图ox轴，取OB上x处微元dx解：连接OA、OB，构成闭合回路OABO，由法拉第电磁感应定律知AB方向B→AVA>VBOx\nEi1Ei2圆柱形均匀的变化磁场产生的感生电场的分布R0，一边长为l的正方形金属框置于磁场中，如图所示，框平面与圆柱形轴线垂直，轴线通过金属框ad边的中点。求：ad、dc和abcda上的电动势。解：Oabcd（1）（3）方向：逆时针方向：d→c\n6.对于单匝线圈取自感系数的定义式为L=／I。当线圈的几何形状、大小及周围磁介质分布不变，且无铁磁性物质时。若线圈中的电流强度变小，则线圈的自感系数L（A）变大，与电流成反比；（B）变小；（C）不变；（D）变大，但与电流不成反比。自感、互感\n7.由麦克斯韦方程组的积分形式确定那一个麦克斯韦方程相当于或包括下列事实：（1）位移电流。[]（2）一个变化的电场，必定有一个磁场伴随它。[]（3）磁感应线是无头无尾的。[]（4）不存在磁单极；[]（5）一个变化的磁场，必定有一个电场伴随它。[]DDCCB（A）（B）（C）（D）麦克斯韦方程组\n解析法机械振动简谐振动（弹簧振子）特征特征量图象法旋转矢量法求解方法能量合成同方向同频率\n8.如图所示，振子放在倾角为的光滑斜面上，弹簧一端固定，则该弹簧振子的周期为mk（A）（B）（C）（D）固有性质\n\n\n9.一个质点作简谐振动,振幅为A，在起始时刻质点的位移为A/2,且向x轴的负方向运动，代表简谐振动的旋转矢量图为t=0X0=A／2V0<0oxωAoxωAoxωAoxωAA.B.C.D.旋转矢量法！！！\n10.一质点沿X轴作简谐振动，振幅A=0.12m，周期T=2s。当t=0时，质点对平衡位置的位移是x0=0.06m，此刻质点向正方向运动。求：（1）谐振动方程；（2）振子第一次通过平衡位置的时刻。ABAOXA/2Ctt+t=0t=t类似题目：教9－14、15、18\n11.一弹簧振子作简谐振动,总能量为E。如果其振幅增加为原来的两倍,振子质量增加为原来的八倍，其他参量不变，则它的总能量变为(A)E/4；(B)E/2；(C)4E；(D)2E。\n12.两个简谐振动的振动方程分别为则合成振动的振动方程为OxA1A2两个同方向,同频率的简谐振动合成后仍为同频率的简谐振动\n机械波简谐波能量波的叠加（干涉）相位依次落后的振动的集合特征量波动方程波源在x＝0处波源在x0处相干条件：频率相同、振动方向相同、相位差恒定相长相消\n波源在坐标原点波源在坐标x=x0处\n13.已知某平面简谐波在t=0时的波形曲线如图所示。波沿x轴正方向传播，已知周期T＝3s，求：（1）坐标轴原点处质点的的振动方程；（2）该波的波动方程。（3）点P处质点的振动方程。t=0y=A／2v>0x=0O点的振动方程x／mOt=0y/cmP240.10.40.8oyωA\nxP=0.8m处质元的振动方程波动方程=4（0.4－0.1）=1.2（m）\n14.如图所示为一平面简谐波在t时刻的波形曲线。若在此时A点处介质质元的振动动能在增大，则A.A点处质元的形变势能在减小；B.B点处质元的振动动能在增大；C.波沿x轴正方向传播；D.C点处质元的形变势能在增大。uxyOACB\n15.一平面简谐波沿x轴正方向传播，t=0时刻的波形图如图所示，则P处质点的振动在t=0时刻的旋转矢量图是xyOPuoyωAoyωAoyωAoyωAA.B.C.D.t=0t=0xp=0v0>0注意：质点下一时刻的运动方向的判断！\n16.一质点作谐振动的振动曲线如图1所示，则质点的初相位1=________；一平面简谐波在t=0时刻的波形曲线如图2所示，则O点处质元的初相位2=__________ytOA/2A图1yxOA/2A图2oyωAoyωA看清楚横轴坐标！分清振动曲线和波动曲线！\n两相干波在P点的相位差:（k=0,1,2,…）（1）干涉相长：=(2k+1)（k=0,1,2,…）（2）干涉相消：S1S2Pr1r2=2k（k=0，1，2…）特例：若2=1，则干涉相长：=k（k=0，1，2…）干涉相消：\n17.S1、S2是振动频率、振动方向均相同的两个点波源，两者相距2／3（如图所示），已知S1的初相位为－／2，求：（1）如果S2C上各点由两列波引起的振动均干涉相长，则S2的初相应为多少？（2）若S1S2连线的中垂线MN上各点由两列波引起的振动均干涉相消，则S2的初相位应为多少？S1S2CMN\nOxS1S2CPr1（1）在S2C连线间任取一点P（k=0）r2\nS1S2CMN（2）在MN连线间任取一点QQr1r2（k=0）\n波动光学等厚干涉双缝干涉偏振衍射惠更斯－菲涅耳原理极小次极大干涉薄膜干涉劈尖单缝衍射三种偏振态起偏检偏N=2kN=2k+1暗纹明纹明纹暗纹光学仪器分辨本领衍射光栅牛顿环↑波带数主极大半角宽主极大线宽←半波损失是否存在？\n光程：光在介质中的几何路程r与折射率n的乘积nr称为光程。光程差相位差为真空中的波长相干条件\n18.在杨氏干涉实验中以钠光灯照射狭缝（=589.3nm）。若将一肥皂膜（n=1.33）放入双缝中S2缝后面的光路中，干涉条纹的中心极大移到原来第二极大处。求：（1）放入肥皂膜后，条纹向哪个方向移动？（2）肥皂膜的厚度？OS1S2r1r2n，dO'r1'r2'k=0k’=0k’=2解:放膜前O点光程差放膜后O点光程差（1）向下移动（2）\nen1n2n3n1>n2>n3n1n3n1>n2n2>n319.（11-13、（17-5））如图所示，用白光垂直照射厚度d=400nm的薄膜，若薄膜的折射率为n2=1.40，且n1>n2>n3。问:反射光中哪种波长的可见光得到加强。（400nm-760nm）解：若n1>n2

查看更多