- 2022-08-16 发布 |
- 37.5 KB |
- 15页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
大学物理驻波课件
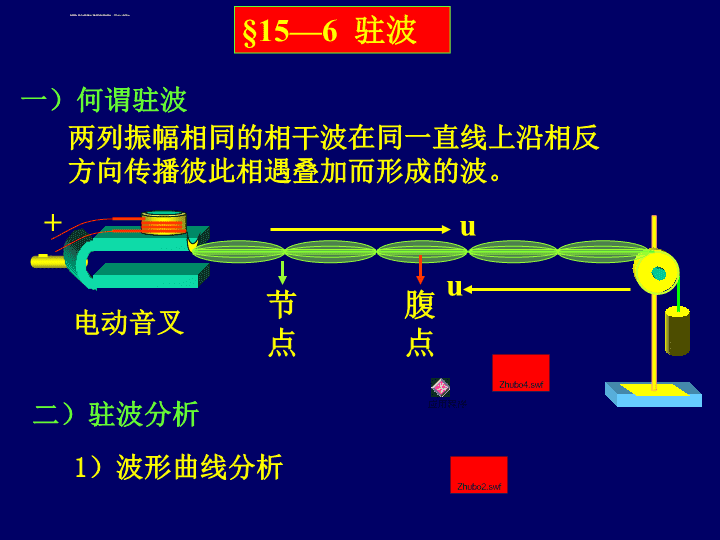
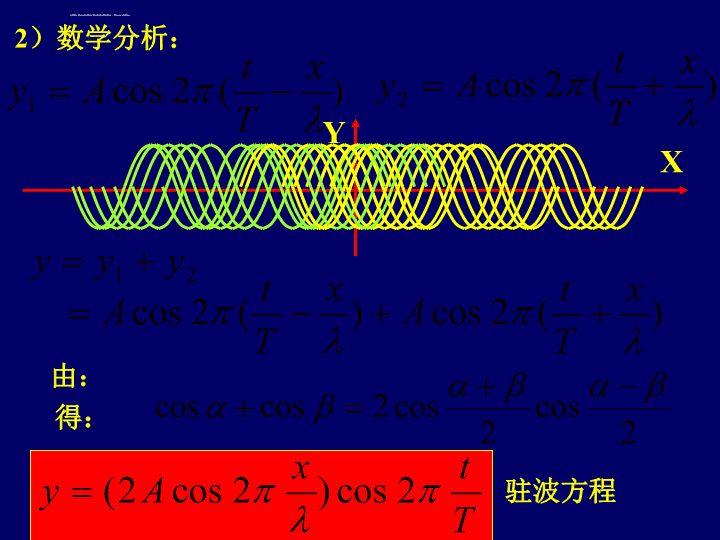
§15—6驻波一)何谓驻波两列振幅相同的相干波在同一直线上沿相反方向传播彼此相遇叠加而形成的波。uu节点二)驻波分析1)波形曲线分析电动音叉+-腹点\n由此可见,驻波特点是:2)相邻两节点间的质点具有相同的相位,节点两侧具有相反的相位。1)驻波波形固定,有波腹点和波节点,且相邻的腹点与腹点,节点与节点间距离为相邻的节点与腹点间的距离为XY\n2)数学分析:XY由:得:驻波方程\nXY驻波方程分析:1驻波波形t1时刻波形:t2时刻波形:t1t2\n驻波方程2质点振动方程X1处质点振动方程:X2处质点振动方程:各处质点振幅不同:\n3腹点与节点位置:腹点取极大值处相邻两腹点间距离为:节点取极小值处相邻两节点间距离为:\nXY4相位关系分析:先看a、b两节点间的质点两节点间质点同相开始计时:obcda再看节点b的两侧质点:节点两侧质点反相\n纵驻波:3)驻波的能量XY驻波中的能流密度为零,实际上是系统的一种稳定的振动状态。\n三)半波损失实验1)反射点为固定端C在反射点出现波节相位突变!相当于=/2半波损失!实验2)反射点自由端uu在反射点出现波腹无半波损失!\n反射波透射波入射波波在两种媒质介面上反射时:u大者为波密介质,u小者为波疏介质若反射波中产生“半波损失”若反射波中无“半波损失”,(从波疏介质进入波密介质)(从波密介质进入波疏介质)\n驻波的应用(了解)(1)作驻波式振动的声源:弦的振动——两端固定波节••L••L••L只有那些半波长的整数倍恰等于弦长的波动,才能在弦中激发起来。即:L=n—22Ln=——n因故n=1,1=2L,基音(基频)A1最大强度最大n=2,2=L,第一泛音……n=k,k=k1A2,A3……较小音调:决定于基音的频率。音色:决定于泛音频率的多少和相对振幅。\nXBlYO例1.一平面波在距反射壁B为l处的振动规律为y=Acost设波速为c(反射时有半波损失)。求:(1)入射波和反射波的表达式;(2)合成后,波节和波腹的位置。解:(1)建立图示坐标,入射波方程xy1=Acos(t—)c在B点(x=l)引起的振动ly1B=Acos(t—)c反射波在B点引起的振动ly2B=Acos[(t—)]c反射波方程(B点为已知点)lxly2=Acos[(t———)]ccx2l=Acos[(t+——)]cc\nXBlYOxy1=Acos(t—)cx2ly2=Acos[(t+——)]cc(2)合成后,波节和波腹的位置。y=y1+y2llx=2Acos[(t—)—]cos[(——)+—]c2c22l=2Asin—(lx)sin(t—)c波节2sin—(lx)=02—(lx)=k波节坐标x=lk—2因xl,所以,k=0,1,2波腹2|sin—(lx)|=12—(lx)=(2k+1)—2波腹坐标x=l(2k+1)/4k=0,1,2\n例2:设波的表达式为x10y=10cos——cos——t。44位于x=1和x=3的两点之相位差。解:求波节位置坐标:xcos——=04x=2(2k+1)x=2,6,10,显然这两点在波节(x=2)两侧,故=。还可将x=1、x=3分别代入,由它们的符号相同与否来判断=0或。\n驻波与行波(1)振幅(2)相位(3)能量随x做周期性变化。波节Amin=0;波腹Amax=2A0;其它处0A2A0不变相邻两节点之间的点同相;节点两侧的点反相。无相位传播,仅在节点处发生相位突变。2(t,x)=t—x+0沿波向逐点落后。沿波向传播能量–1P=—u2A2S2无能量传播。能量时而集中在波节,时而集中在波腹。••••查看更多