- 2022-08-16 发布 |
- 37.5 KB |
- 21页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
大学物理作业课件
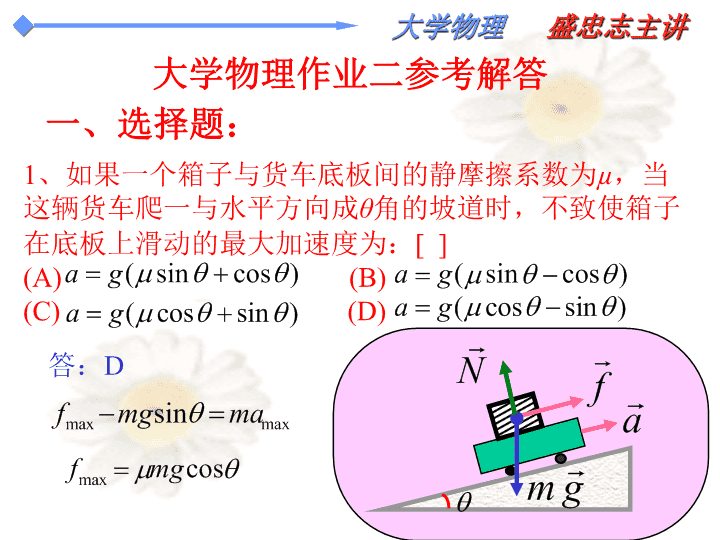
大学物理作业二参考解答一、选择题:答:D1、如果一个箱子与货车底板间的静摩擦系数为µ,当这辆货车爬一与水平方向成θ角的坡道时,不致使箱子在底板上滑动的最大加速度为:[](A) (B)(C) (D)\n答:B2、质量为0.25kg的质点,受的力作用,当时,该质点以的速度通过坐标原点,该质点任意时刻的速度是:[](A)(B)(C)(D)\n3、对于一个物体系来说,在下列条件中,那种情况下系统的总动量守恒?[](A)合外力为零。(B)合外力矩为零。(C)合外力不作功。(D)外力和保守内力都不作功。4、物体B的质量是物体A的质量的4倍,它们在光滑水平面上运动,开始时物体A的速度为,物体B的速度为;在无外力作用的情况下两者发生完全非弹性碰撞,碰后物体B的速度为:[](A)(B)(C)(D)。答:A答:A\n5、对功的概念有以下几种说法:(1)保守力作正功时,系统内相应的势能增加。(2)质点运动经一闭合路径,保守力对质点作的功为零。(3)作用力和反作用力大小相等、方向相反,所以两者所作功的代数和必为零。在上述说法中:[](A)(1)、(2)是正确的。(B)(2)、(3)是正解的。(C)只有(2)是正确的。(D)只有(3)是正确的。答:C答:B6、质量的物体,从坐标原点处由静止出发在水平面内沿X轴正向运动,所受的合力为。物体在处的速度大小为[](A)3m/s(B)6m/s(C)9m/s(D)12m/s。\n答:B7、对于一个物体系来说,在下列条件中,那种情况下系统的机械能守恒?[](A)合外力为零。(B)外力和非保守内力都不作功。(C)合外力不作功。(D)外力和保守内力都不作功。8、物体的质量为3kg,时位于,,若一恒力矩作用在物体上,时,物体对Z轴的角动量大小是:[](A)15kg.m2/s(B)45kg.m2/s(C)60kg.m2/s(D)75kg.m2/s。答:D\n9、哈雷慧星绕太阳的轨道是以太阳为一个焦点的椭圆,它离太阳最近的距离是r1=8.75×1010m,此时它的速率是V1=5.46×104m·s-1。它离太阳最远的速率是V2=9.08×102m·s-1,这时它离太阳的距离是r2=[]。(A)5.26×1010m(B)5.26×1011m(C)5.26×1012m(D)5.26×1013m。答:C\n1、质量为0.25kg的质点,在水平面内沿X轴正向运动,受的力作用,时该质点以的速度通过坐标原点,质点任意时刻的速度v=_____,质点任意时刻的位置坐标x=_________。二、填空题:\n2、初速度为,质量为m=0.05kg的质点,受到冲量的作用,则质点的末速度为。3、一颗速率为的子弹,打穿一木板后速率降为。如果让它继续穿过与第一块完全相同的第二块木板,穿过后,子弹的速率为。\n5、质量为的质点,在外力的作用下沿轴运动,已知时,质点位于原点,且初速度为零。质点在处的速率为。4、某质点在力(SI)的作用下,沿直线从点(0,0)移动到点(3m,3m)的过程中,力所做功为__________。\n7、质量为m的质点位于处,速度为。则它对坐标原点的角动量为。6、质量为4.25Kg的质点,在合力的作用下,由静止从原点运动到时,合力所做的功为;此时质点的运动速度大小为。34J\n8、物体的质量为3kg,时,若力作用在物体上,则内物体所受的冲量为。末时,物体的速度为。\n三、计算题:解:即:根据牛顿第二定律,汽艇的运动方程为:分离变量:选择汽艇开始在阻力作用下作减速运动时的位置为坐标原点,汽艇滑行的方向为x轴的正方向。于是,初始条件可写为:当时,,。1、质量为,速度为的汽艇,在关闭发动机情况下沿直线滑行,若汽艇所受阻力与速率的平方成正比例,即,为正常数。试求汽艇速度和路程随时间的变化规律。\n积分:再由:即:积分:\n解:①由牛顿第二定律,得:即:2、质量为2kg的质点,在力作用下,作平面运动。在t=0,这个质点在处,其速度为。求:①质点在任意时刻的速度。②质点的运动方程。③轨道方程。\n②:由:③:消去t,得:质点做匀速圆周运动\n解:(1)以桌边为坐标原点,向下为y轴正方向。设下垂的长度为y,此时摩擦力的大小为做功:3、一链条总长为l,质量为m,放在桌面上,并使其下垂,下垂一端的长度为a,设链条与桌面之间的滑动摩擦系数为,令链条由静止开始运动,则:(1)链条离开桌面的过程中,摩擦力对链条作了多少功?(2)链条离开桌面时的速率是多少?\n(2)对整个链条来说,质点系受到两个外力作用:摩擦力和下垂部分的重力根据动能定理:\n4、一质量为m的小球,由顶端沿质量为M的圆弧形木槽自静止下滑,设圆弧形槽的半径为R(如图所示)。忽略所有摩擦,求:(1)小球刚离开圆弧形槽时,圆弧形槽的速度。(2)此过程中,圆弧形槽对小球所做的功。MRmAB解:(1)设小球和圆弧形槽的速度分别为v和V,水平方向动量守恒,有:以地球,小球和圆弧形槽为系统,机械能守恒,有:\n(2)设圆弧形槽对小球所做的功为W,由动能定理:\n5、如图所示,一轻质弹簧劲度系数为k,两端各固定一质量均为M的物块A和B,放在水平光滑桌面上静止。今有一质量为m的子弹沿弹簧的轴线方向以速度v0射入一物块而不复出,求此后弹簧的最大压缩长度。解:第一阶段:子弹射入到相对静止于物块A。由于时间极短,可认为物块A还没有移动,应用动量守恒定律,求得物块A的速度vAABv0m\n第二阶段:物块A移动,直到物块A和B在某舜时有相同的速度,弹簧压缩最大。应用动量守恒定律,求得两物块的共同速度v应用机械能守恒定律,求得弹簧最大压缩长度查看更多