- 2022-08-16 发布 |
- 37.5 KB |
- 24页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
大学物理(振动学)
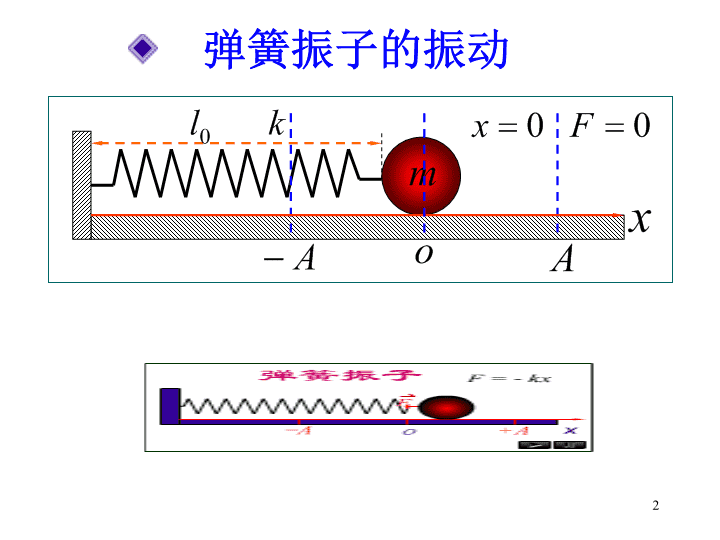
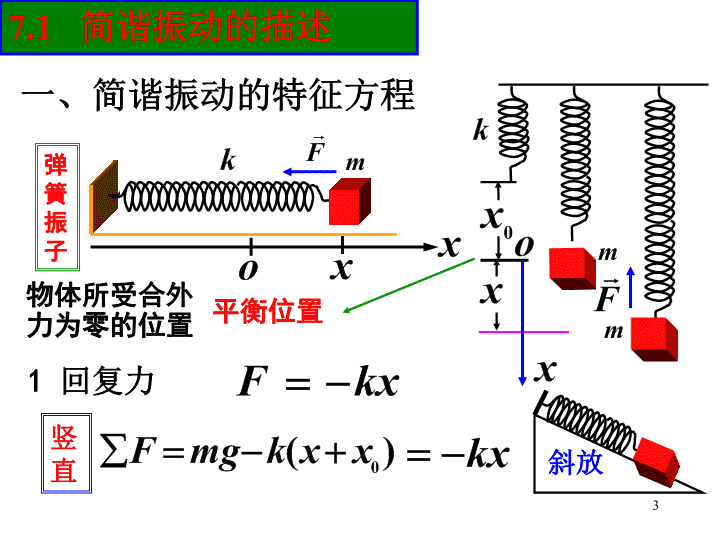
一切波动都是某种振动的传播过程物体在某一位置附近所作的来回往复的运动复杂振动任何一个物理量随时间的周期性变化即为振动机械振动:广义:振动是波动的基础:=第七章振动1\n弹簧振子的振动2\n弹簧振子一、简谐振动的特征方程平衡位置1回复力物体所受合外力为零的位置竖直斜放7.1简谐振动的描述3\n2简谐振动的微分方程(动力学方程)0x4\n3简谐振动的运动方程加速度振幅速度振幅(振动方程)5\n三条特征简谐振动三条判据简谐振动的定义式简谐振动的普遍定义式6\n二点说明坐标原点取在平衡位置(2)证明一种振动是简谐振动的一般步骤a)确定研究对象,找平衡位置b)建立以平衡位置为原点的坐标系c)进行受力分析d)利用牛顿定律或转动定律写出物体在任一位置的动力学方程e)根据判据判断该振动是否为简谐振动(1)特征方程成立的条件:7\n二描述简谐振动的物理量2周期频率圆频率完成一次全振动所用时间回到原来的运动状态单位时间内全振动的次数2π个单位时间内全振动的次数1、振幅:表示物体离开平衡位置的最大距离——A8\n(1)建立振动系统的微分方程弹簧振子求一个振动系统固有ω、T、的方法9\n3、位相和初相(1)位相:(相位、周相、相)(2)初相:不同的位相表示不同的运动状态初相不同,物体的初始运动状态不同表示物体的运动状态10\n(3)对位相作四点说明a)用位相表征物体的振动状态,可以反映振动的周期性b)若已知位相差△,可以求出同一简谐振动由一个状态变化到另一状态所经历的时间△tc)利用位相差比较两个同方向、同频率简谐振动的步调x1=A1cos(ωt+1)x2=A2cos(ωt+2)当△=±2kπ(k=0,1,2,…)两振动步调一致,同相当△=±(2k+1)π(k=0,1,2,…)两振动步调相反,反相d)位相也可以用来比较不同物理量的步调11\n三、振幅和初相的确定当t=0时确定的方法:x0=Acosx=x0x0=Acos或由的正负,根据确定cos或sin的正、负,从而确定所在的象限初始条件12\n四、简谐振动的描述方法2.图线法(振动曲线)1.解析法13\n旋转矢量的端点在轴上的投影点的运动为简谐运动.旋转矢量法演示14\n3.旋转矢量法t=0x.otxA振幅矢量(2)圆周运动的半径参考圆绕O点以角速度逆时针旋转的矢量A,在x轴上的投影正好描述了一个简谐振动等于振动的园频率(1)圆周运动的角速度(3)圆周的矢径与x轴夹角等于振动的振幅初始时刻等于振动的初相(4)已知质点的运动状态,(或振动曲线)能画出振幅矢量的位置,从而确定该时刻位相任意时刻等于振动的位相注意几个问题:15\n..oA方法:(a)取ox轴(沿振动方向)(b)作参考圆:以o为圆心,振幅A为半径作一圆周(c)在x轴(振动轴)上找出与质点运动状态的对应点(d)作振幅矢量:过与质点运动状态对应点作x轴的垂线,与参考圆相交两点,从原点o向这两点作向量,根据速度方向确定振幅矢量的位置(e)该振幅矢量与x轴正向夹角就是该时刻的位相例1:16\n一质点沿x轴作简谐运动,A=0.12m,T=2s,当t=0时质点对平衡位置的位移x0=0.06m向x轴正向运动。求:(1)简谐运动表达式;(2)t=T/4时,质点的位置、速度、加速度;(3)第一次通过平衡位置的时刻。解:(1)A/20=?例题217\n(2)t=T/4时,质点的位置、速度、加速度;18\n(3)第一次通过平衡位置的时刻还可以求“第二次……”——旋转角度11/6平衡位置19\n例:单摆1、细线质量不计3、阻力不计约定解:受力:取逆时针为正力矩:20\n已知简谐振动表达式xA试画出振动曲线0tx例题321\n小结一、简谐振动的特征方程1。回复力2。简谐振动的微分方程(动力学方程)3。简谐振动的运动方程(振动方程)掌握证明一种振动是简谐振动的一般步骤22\n二、描述简谐振动的物理量1、振幅:2、周期(T):(A)[频率(γ)、圆频率(ω)]弹簧振子求振幅有三种方法(1)已知初始位速(3)已知总机械能(2)已知任意位速23\n求圆频率的方法(1)建立振动系统的微分方程(2)利用公式求(3)利用速度和加速度幅值求3、位相和初相①已知状态求位相(表示物体运动状态的物理量)②已知位相求状态③已知位相差求时间差(1)位相(2)求初相方法①解析法(利用初始条件)②旋转矢量法24查看更多