- 2022-08-16 发布 |
- 37.5 KB |
- 5页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
大学物理清考
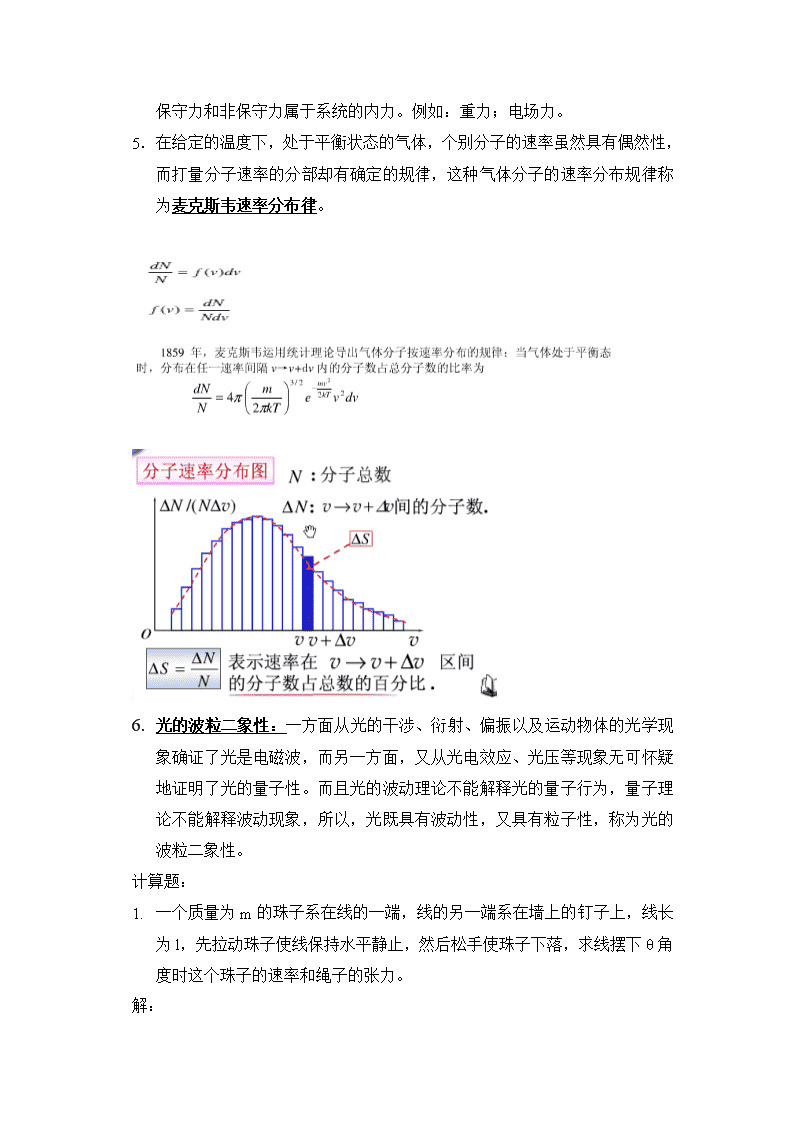
1.在确定的平面上质点的运动轨迹为圆周的运动成为圆周运动。角加速度:角位移△θ与对应时间之比ω=△θ/△t称为△t时间内的平均叫速度。当△t→0时,平均角速度的极限称为质点在t时刻对应的瞬时角速度(简称角速度)。2.线量和角量的关系:s=Rθ,V=Rω,aτ=Rβ.an=Rω2。3.简谐振动的三要素:振幅A,圆频率ω,初相位φ。4.物理量:一类:描述过程二类:过程量(位移、冲量)状态量(速度)。5.热力学第二定律开尔文表述为:不可能创造一种循环动作的热机,只从一个热源吸收热量,使之完全变为有用的功而不产生其他影响。克劳修斯表述:热量不能自动地从低温物体传向高温物体。6.电场线:切线方向代表电场方向电场线的疏密代表电场强弱。磁场:洛伦兹力永不做功,只改变电荷的运动方向。7.楞次定律是能量守恒和转化定律在电磁感应现象上得具体现象。8.自由度:为了确定物体在空间二位置,引入独立坐标二数目—。9.自由度均分原理:在温度为T的平衡态下,气体分子每个自由度的平均动能都相等,且等于kT.影响气体在平衡状态下自由度都是相等—按自由度均分原理。10.光的特性:\n一方面从光的干涉、衍射、偏振以及运动物体的光学现象确证了光是电磁波,而另一方面,又从光电效应、光压等现象无可怀疑地证明了光的量子性。而且光的波动理论不能解释光的量子行为,量子理论不能解释波动现象,所以,光既具有波动性,又具有粒子性,称为光的波粒二象性。干涉的条件:固频率、有固定的相位差、光矢量方向不垂直11.多普勒效应:波源(或观测者,或两者)相对于媒质运动,而使观察者接受到的波的频率发生变化的现象。12.机械波形成过程:形成机械波,首先要有做机械振动的物体,即波源:其次还要有能够传播机械振动的弹性媒质。波源和弹性媒质是产生机械波的两个必须具备的条件。机械波的传播:波源的振动状态向外传播简答题:1.理想模型:质点、刚体、理想气体、弹簧振子、单摆、点电荷等2.花样滑冰表现为角动量守恒定律:转动惯量J增大时,角速度ω减小;转动惯量J减小时,角速度ω增大。对一固定点o,质点所受的合外力矩为零,则此质点的角动量矢量保持不变。3.宇宙速度:1.环绕速度2.挣脱速度3.逃逸速度第一宇宙速度也是人造卫星在地面附近绕地球做“匀速圆周运动”所必须具有的速度。但是随着高度的增加,地球引力下降,环绕地球飞行所需要的飞行速度也降低,所有航天器都是在距地面很高的大气层外飞行,所以它们的飞行速度都比第一宇宙速度低。同时第一宇宙速度又称为环绕速度。第一宇宙速度的计算公式是:V1=√(gR)(m/s),其中g=9.8(m/s^2),R=6.4×10^6(m)。V=7.9km/s第二宇宙速度(V2)当航天器超过第一宇宙速度V1达到一定值时,它就会脱离地球的引力场而成为围绕太阳运行的人造行星,这个速度就叫做第二宇宙速度,亦称脱离速度。按照力学理论可以计算出第二宇宙速度V2=11.2km/s.第三宇宙速度如果想使物体挣脱太阳系引力的束缚,飞到太阳系以外的宇宙空间去,必须使它的速度等于或者大于16.7千米/秒,即第三宇宙速度。4.若某种力做功仅与起末位置有关而与路径无关,则这种力称为保守力;把不具有这种特性的力称为非保守力\n。把保守力存在的空间称为保守力场;保守力和非保守力属于系统的内力。例如:重力;电场力。1.在给定的温度下,处于平衡状态的气体,个别分子的速率虽然具有偶然性,而打量分子速率的分部却有确定的规律,这种气体分子的速率分布规律称为麦克斯韦速率分布律。1.光的波粒二象性:一方面从光的干涉、衍射、偏振以及运动物体的光学现象确证了光是电磁波,而另一方面,又从光电效应、光压等现象无可怀疑地证明了光的量子性。而且光的波动理论不能解释光的量子行为,量子理论不能解释波动现象,所以,光既具有波动性,又具有粒子性,称为光的波粒二象性。计算题:1.一个质量为m的珠子系在线的一端,线的另一端系在墙上的钉子上,线长为l,先拉动珠子使线保持水平静止,然后松手使珠子下落,求线摆下θ角度时这个珠子的速率和绳子的张力。解:\n两次同时取定积分(摆角从0→θ,速率从0→v)得,珠子在任意时刻,牛顿第二运动定律的法向分量方程为:所以T=3mgsinθ,这就是线中得张力。1.求均匀带电细棒中垂面上的场强分布,设棒长为L,带点总量为q(q<0).解:dydEaαdEXαPdEdya如图,选取细棒中点0为坐标原点。由于细棒均匀带点,电荷线密度为λ=q/l,在细棒上任取一小电荷微元dq,由于细棒具有对称性,则总可以找到与之对称的另一电荷微元dpa,两个微元所带的电量为dq=dqa=λ\ndy,它们在P点产生的场强dE和dEa关于中垂线对称,两者的合场强沿X轴正方向,即E=Exi(Ey=0),所以只需求Ex,有:又图可知:根据场强的叠加原理:当X《L时,即在带电细棒中部附近区域内:当X》L时,即在远离带电细棒的区域内:1.长度为L的一根铜棒在均匀磁场B中绕其一端O以角速度ω做均匀角速度转动,且转动平面与磁场方向垂直,求铜棒两端的电势差。解:在距O点为L处取一线元dl,其大小为v=ωl,所产生的电动势为:铜棒两端的电势差为:查看更多