- 2022-08-16 发布 |
- 37.5 KB |
- 24页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
大学物理刚体的转动
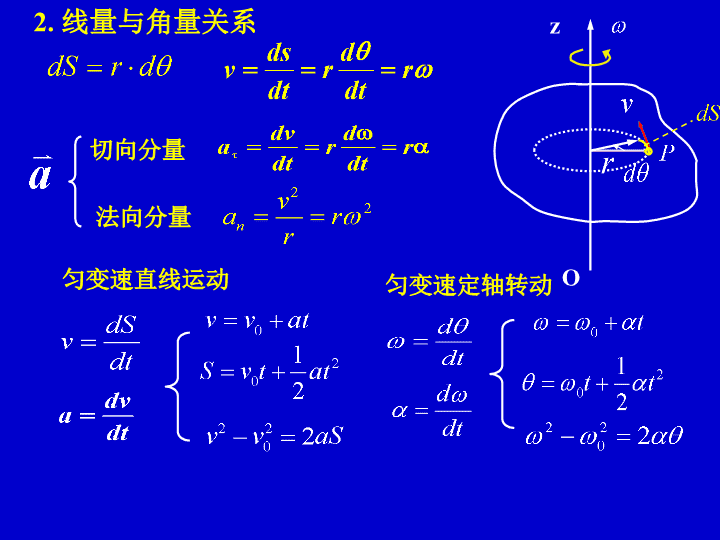
第三章刚体的转动3.1刚体的运动一、刚体的平动在运动过程中刚体上的任意一条直线在各个时刻的位置都相互平行ABA’B’B”A”刚体的平动任意质元运动都代表整体运动二、刚体的定轴转动刚体所有质元都绕一固定直线(定轴)作圆周运动刚体的平动、定轴转动和复合运动用质心运动代表刚体的平动(质心运动定理)刚体:受力时不改变形状和体积的物体。\n用角量描述转动1)角位移θ:在t时间内刚体转动角度2)角速度:3)角加速度α:θz刚体定轴转动角速度的方向按右手螺旋法则确定1.\n切向分量法向分量zO2.线量与角量关系匀变速直线运动匀变速定轴转动\n3.2刚体定轴转动定律质点系的角动量定理Z轴分量质元对O点的力矩(垂直z轴)zO(垂直z轴)1.刚体定轴转动定律\nzO质元到转轴的垂直距离转动惯量对固定轴\n刚体定轴转动定律与牛顿第二定律对比:刚体到转轴的转动惯量:转动惯量的物理意义:1.刚体转动惯性大小的量度;2.转动惯量与刚体的质量有关;3.J在质量一定的情况下与质量的分布有关;4.J与转轴的位置有关。对比刚体的角动量和质点的动量:与对应\n二、刚体转动惯量的计算称为刚体对转轴的转动惯量对质量连续分布刚体线分布面分布体分布是质量的线密度是质量的面密度是质量的体密度\n例:一均匀细棒长l质量为m1)轴z1过棒的中心且垂直于棒2)轴z2过棒一端且垂直于棒求:上述两种情况下的转动惯量oZ1解:棒质量的线密度所以只有指出刚体对某轴的转动惯量才有意义oZ2lXX\n例:匀质圆盘绕垂直于盘面通过中心轴的转动惯量如下图:解:圆盘半径为R,总质量为m.设质量面密度例:匀质圆环半径为R,总质量为m,求绕垂直于环面通过中心轴的转动惯量如下图:ZRdm解:ZRrdrdmdSm\n1.有关转动惯量计算的几个定理:2)平行轴定理Zh式中:关于通过质心轴的转动惯量m是刚体质量,h是c到Z轴的距离是关于平行于通过质心轴的一个轴的转动惯量C1)转动惯量叠加ACZ式中:是A球对z轴的转动惯量是B棒对z轴的转动惯量是C球对z轴的转动惯量B\n3)垂直轴定理0对于薄板刚体,薄板刚体对z轴的转动惯量等于对x轴的转动惯量与对y轴的转动惯量之和。\n2.刚体定轴转动定律的应用解:滑轮加速转动,由转动定律得:线量与角量关系:已知:滑轮M(看成匀质圆盘)半径R物体:m求:a=?1.RmamgTTMω物体m加速运动:\nRm1m2已知:滑轮M(看成匀质圆盘)半径R物体:m1m2求:a=?am1gm2gT解:对否?T2T否则滑轮静止或匀速转动,而物体加速运动T1T2转动定律线量与角量关系M2.T1\nθmO已知:例3.2匀质杆m长下落到θ时求:解:C转动定律θθ对上式两边分别乘以dθ,再进行积分得:\n质心运动定理:θmOCθθβ例3.3答案:转到竖直位置时:F=5mg/2(θ=90°)\n三、刚体定轴转动中的动能定理OθdθrP刚体的转动动能定轴转动动能定理\n已知:匀质杆M子弹m水平速度求:射入不复出解:对M,m系统:系统角动量守恒匀质杆的质心速度设杆长为合外力为零,系统动量守恒。对否?lω,,最大摆角θOMmcω\nOMmcθ在碰撞过程中,子弹和细棒的总机械能不守恒。但碰撞后,在子弹随细棒摆动过程中,只有重力做功,因此系统机械能守恒。以转轴处为势能零点。由始末状态机械能相等得:\n3.3刚体的复合运动在以上对于刚体动力学的讨论中,得到两个结论:2.刚体的定轴转动定律:1.质心运动定律:F是刚体所受合外力,ac是刚体质心加速度,m是刚体的质量。M是刚体所受合外力矩,α是刚体绕定轴转动的角加速度,J是刚体的定轴转动惯量。刚体的复合运动:可以分解为刚体的平动和刚体绕质心轴的转动\n一、质心系的角动量定理以质心O’为原点的参考系称为质心参考系。设惯性系的原点为O质心系的角动量定理:是质点系中各质点所受外力对质心的力矩的矢量和即质点系的角动量定理在质心系中仍然成立。是质点系中各质点对质心的角动量之和所以原来只对定轴转动成立的转动定律,对于通过质心的转轴仍然成立\n二、柯尼希定理质点系相对于惯性系的总动能等于质点系的轨道动能和内动能之和。考虑到重力势能,有:对于刚体有:\n例3.5如图,质量为m,半径为R的圆柱体沿斜面向下无滑动地滚动,试求它到达斜面下端时质心的速率。hNfmgs解法一.用能量守恒求解。ω是圆柱体在斜面底端时绕质心的角速率;\n例3.5如图,质量为m,半径为R的圆柱体沿斜面向下无滑动地滚动,试求它到达斜面下端时质心的速率。hNfmgs解法二.用转动定律求解。在垂直斜面方向上:\no方向与方向相同dt时间内轴转过角omg重力矩:M=mgr角动量定理:三、角动量守恒和进动进动:高速自旋物体的转轴在空间转动的现象称为进动查看更多