《大学物理》概念-11页

《大学物理》概念-11页

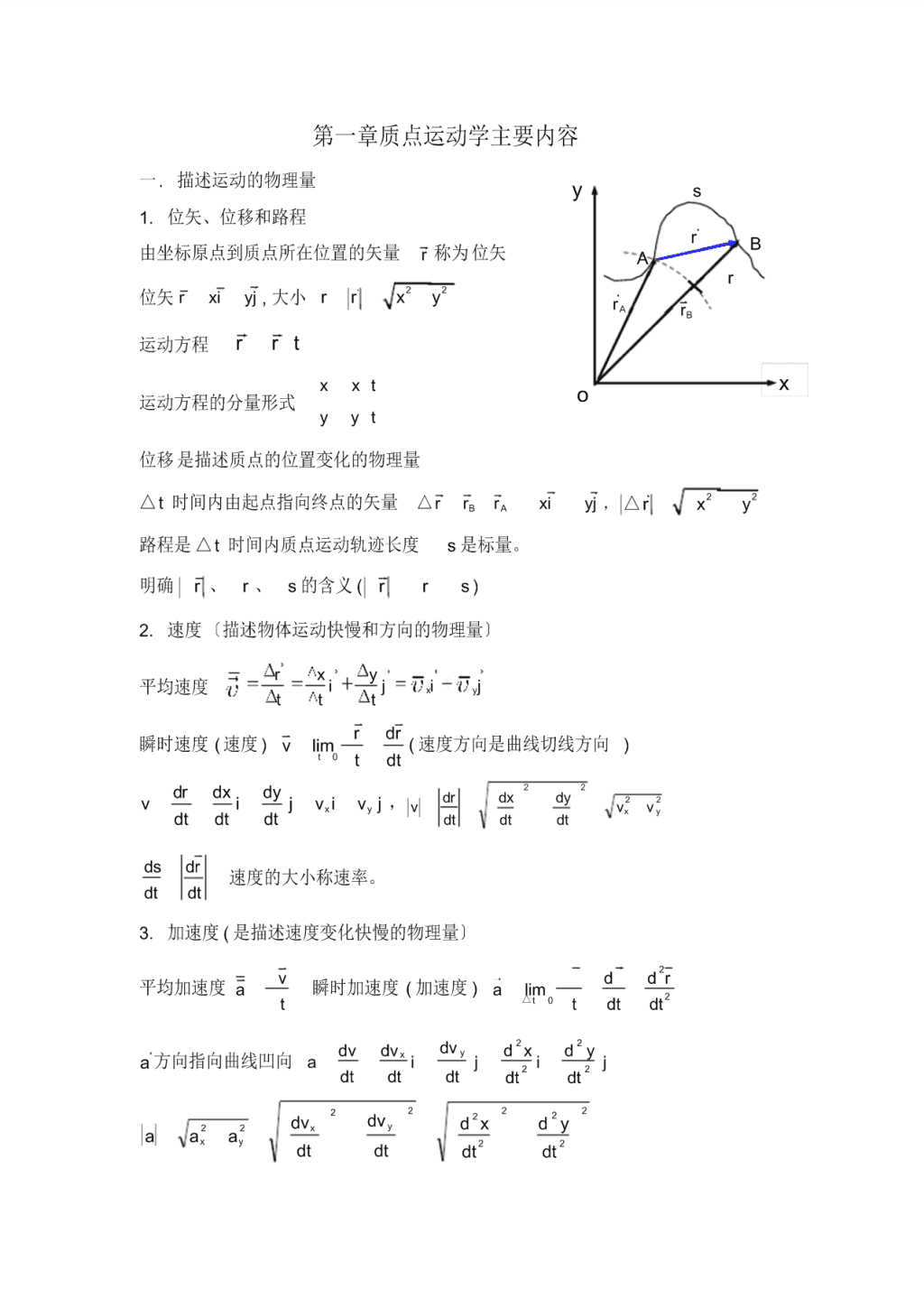
第一章质点运动学主要内容一.描述运动的物理量ys1.位矢、位移和路程rB由坐标原点到质点所在位置的矢量r称为位矢Ar22位矢rxiyj,大小rrxyrArB运动方程rrtxxtxo运动方程的分量形式yyt位移是描述质点的位置变化的物理量22△t时间内由起点指向终点的矢量△rrBrAxiyj，△rxy路程是△t时间内质点运动轨迹长度s是标量。明确r、r、s的含义(rrs)2.速度〔描述物体运动快慢和方向的物理量〕rxy平均速度ijxiyjtttrdr瞬时速度(速度)vlim(速度方向是曲线切线方向)t0tdtdrdxdy22vijvivj，drdxdy22xyvvxvydtdtdtdtdtdtdsdr速度的大小称速率。dtdt3.加速度(是描述速度变化快慢的物理量〕2vddr平均加速度a瞬时加速度(加速度)alimt△t0tdtdt222dvdvxdvydxdya方向指向曲线凹向aijij22dtdtdtdtdt22222222dvxdvydxdyaaxay22dtdtdtdt\n12运动方程矢量式为rv0tgt2xv0cost(水平分运动为匀速直线运动)分量式为12yv0sintgt(竖直分运动为匀变速直线运动)2三.圆周运动(包括一般曲线运动)ds1.线量：线位移s、线速度vdtdv切向加速度at(速率随时间变化率)dt2v法向加速度an(速度方向随时间变化率)。Rd12.角量：角位移(单位rad)、角速度(单位rads)dt2dd2角速度(单位rads)2dtdt23.线量与角量关系：sR、v=R、atR、anR4.匀变速率圆周运动：vvatt001212(1)线量关系sv0tat(2)角量关系0tt222222vv02as02第二章牛顿运动定律主要内容一、牛顿第二定律dp物体动量随时间的变化率等于作用于物体的合外力即：F=FidtdPdmvdVF=，m常量时F=m或F=madtdtdt说明：(1)只适用质点；(2)F为合力；(3)a与F是瞬时关系和矢量关系；\n(4)解题时常用牛顿定律分量式Fxmax〔平面直角坐标系中〕Fma(一般物体作直线运动情况)Fymay2vFmam（法向）nn〔自然坐标系中〕Fmar(物体作曲线运动)dvFmam（切向）ttdt运用牛顿定律解题的根本方法可归纳为四个步骤运用牛顿解题的步骤：1〕弄清条件、明确问题〔弄清条件、明确所求的问题及研究对象〕2〕隔离物体、受力分析〔对研究物体的单独画一简图，进行受力分析〕3〕建立坐标,列运动方程〔一般列分量式〕；4)文字运算、代入数据举例：如下图，把质量为m10kg的小球挂a0在倾角30的光滑斜面上，求1(1)当斜面以ag的加速度水平向右运动时，3(2)绳中张力和小球对斜面的正压力。解：1)研究对象小球2〕隔离小球、小球受力分析yNFT3〕建立坐标,列运动方程〔一般列分量式〕；xx:FTcos30Nsin30ma(1)y:FTsin30Ncos30mg0(2)P4)文字运算、代入数据1x:3FTN2ma(ag)(3)3y:FT3N2mg(4)131FTmg(1)109.81.57777.3N232\nmg109.8NFTtg3077.30.57768.5Ncos300.866(2)由运动方程，N=0情况x:FTcos30maomy:FTsin30=mga=gctg309.83172s第三章动量守恒和能量守恒定律主要内容一.动量定理和动量守恒定理1.冲量和动量t2IFdt称为在t1t2时间内,力F对质点的冲量。t1质量m与速度v乘积称动量Pmvt22.质点的动量定理：IFdtmv2mv1t1t2IxFxdtmv2xmv1xt质点的动量定理的分量1式：t2IyFydtmv2ymv1yt1t2IzFzdtmv2zmv1zt1nnnt2ex3.质点系的动量定理：Fdtmivimi0vi0PP0t1iiiIxPxPox质点系的动量定理分量式IyPyPoyIzPzPozdP动量定理微分形式，在dt时间内：FdtdP或F=dt4.动量守恒定理：当系统所受合外力为零时，系统的总动量将保持不变，称为动量守恒定律nnnF外=Fi0,则mivi=mi0vi0=恒矢量i1ii\n若Fx0,则　mivixC1恒量i动量守恒定律分量式：若Fy0,则miviyC2恒量i若F0,则mvC恒量ziiz3i二.功和功率、保守力的功、势能1.功和功率：bb质点从a点运动到b点变力F所做功WFdrFcosdsaa恒力的功：WFcosrFrdw功率：pFcosvFvdt物体沿任意路径运动一周时，保守力对它作的功为零WcFdr0l保守力功等于势能增量的负值，wEpEp0Ep物体在空间某点位置的势能Epx,y,zEp00Ep(x,y,z)FdrEp00A(x,y,z)11万有引力作功：wGMmrbra重力作功：wmgybmgya1212弹力作功：wkxbkxa22三.动能定理、功能原理、机械能守恒守恒1.动能定理1212质点动能定理：Wmvmv022质点系动能定理：作用于系统一切外力做功与一切内力作功之和等于系统动能的增量nnnnexin1212WiWimvimvi0iii2i22.功能原理：外力功与非保守内力功之和等于系统机械能〔动能+势能〕的增量\nexinWWncEE0机械能守恒定律：只有保守内力作功的情况下，质点系的机械能保持不变exinexin当WWnc0WW(EE)(EE)nckpk0p0第五章机械振动主要内容一.简谐运动振动：描述物质运动状态的物理量在某一数值附近作周期性变化。机械振动：物体在某一位置附近作周期性的往复运动。简谐运动动力学特征：Fkx2简谐运动运动学特征：ax简谐运动方程：xAcos(t)dx简谐振动物体的速度：vAsintdt2dx2加速度aAcost2dt2速度的最大值vmA，加速度的最大值amA二.描述谐振动的三个特征物理量22v01.振幅A：Ax02，取决于振动系统的能量。22.角(圆)频率：2，取决于振动系统的性质Tkg对于弹簧振子、对于单摆ml3.相位——t，它决定了振动系统的运动状态〔x,v〕v0t0的相位—初相arctgx0所在象限由x0和v0的正负确定：v0v0x00，v00，在第一象限，即取(0)2v0v0x00，v00，在第二象限，即取()23x00，v00，在第三象限，即取()22\n3x00，v00，在第四象限，即取(2)2三.旋转矢量法简谐运动可以用一旋转矢量〔长度等于振幅〕的矢端在Ox轴上的投影点运动来描述。1.A的模A=振幅A,2.角速度大小=谐振动角频率3.t0的角位置是初相4.t时刻旋转矢量与x轴角度是t时刻振动相位tOx轴上的投影点速度和加速度是谐振动的速度和加速度。以弹簧振子为例：121212212EEkEpmvkxmAkA2222设x1A1cost1x2A2cost2xx1x2Acos(t)合成振动振幅与两分振动振幅关系为：AA1A222AA1A22AA12cos(21)A1sin1A2sin2tgA1cos1A2cos2合振动的振幅与两个分振动的振幅以及它们之间的相位差有关。222kk012AA1A22AA12A1A222(2k1)k012AA1A22AA12A1A2一般情况，相位差21可以取任意值A1A2AA1A2\n第六章机械波主要内容一.波动的根本概念1.机械波：机械振动在弹性介质中的传播。2.波线——沿波传播方向的有向线段。波面——振动相位相同的点所构成的曲面T：与质点的振动周期相同。4.波长：振动的相位在一个周期内传播的距离。5.振动相位传播的速度。波速与介质的性质有关二.简谐波沿ox轴正方向传播的平面简谐波的波动方程xtxyAcos[(t)]Acos[2()]uTyxvAsin[(t)]质点的振动速度tuv2x质点的振动加速度aAcos[(t)]tu这是沿ox轴负方向传播的平面简谐波的波动方程。txyAcos2()T两列波频率相同，振动方向相同，相位相同或相位差恒定，相遇区域内出现有的地方振动始终加强，有的地方振动始终减弱叫做波的干预现象。两列相干波加强和减弱的条件：r2r1〔1〕2122k(k0,1,2,)时，AA1A2〔振幅最大，即振动加强〕r2r12122k1(k0,1,2,)时，AA1A2〔振幅最小，即振动减弱〕〔2〕假设21〔波源初相相同〕时，取r2r1称为波程差。r2r12k(k0,1,2,)时，AA1A2〔振动加强〕r2r12k1(k0,1,2,)时，AA1A2〔振动减弱〕；2其他情况合振幅的数值在最大值A1A2和最小值A1A2之间。\n第七章气体动理论主要内容一.理想气体状态方程：PVPV11PV22mC；PVRT；PnkTTT1T2M23231R8.31J；k1.3810J；NA6.02210mol；RNAkkmolk二.理想气体压强公式212pnktktmv分子平均平动动能32三.理想气体温度公式123ktmvkT22四.能均分原理1.自由度：确定一个物体在空间位置所需要的独立坐标数目。2.气体分子的自由度单原子分子(如氦、氖分子)i3；刚性双原子分子i5；刚性多原子分子i63.能均分原理：在温度为T的平衡状态下，气体分子每一自由度上具有的平均1动都相等，其值为kT2i4.一个分子的平均动能为：kkT2五.理想气体的内能〔所有分子热运动动能之和〕i1.1mol理想气体ERT2im3.一定量理想气体ERT()2M第八章热力学根底主要内容一.准静态过程〔平衡过程〕系统从一个平衡态到另一个平衡态，中间经历的每一状态都可以近似看成平衡态过程。二.热力学第一定律QEW；dQdEdWV2WPdvV12.Q,E,W符号规定mmi3.dECVmdT　　或E2E1CVm(T2T1)CVmRMM2\n三.热力学第一定律在理想气体的等值过程和绝热过程中的应用1.等体过程W0QECVm(T2T1)2.等压过程Wp(V2V1)R(T2T1)QEWCpm(T2T1)i2CpmCCRR,　　　热容比＝1pmVm2CVm3.等温过程E2E10mV2mp2QWRTlnRTlnTTMVMp114.绝热过程Q0WECVm(T2T1)-11绝热方程PVC1，VTC2，PTC3。特点：系统经历一个循环后，E0系统经历一个循环后Q（代数和）W（代数和）1.正循环〔顺时针〕-----热机逆循环〔逆时针〕-----致冷机2.热机效率：WQQQ1221QQQ111式中：Q1------在一个循环中，系统从高温热源吸收的热量和；Q2------在一个循环中，系统向低温热源放出的热量和；W＝Q1－Q2------在一个循环中，系统对外做的功〔代数和〕。T23.卡诺热机效率:c1T1式中：T1------高温热源温度；T2------低温热源温度；\n4.制冷机的制冷系数：Q2Q2定义：e=WQ1-Q2Q2T2卡诺制冷机的制冷系数：eQ1Q2T1T2五.热力学第二定律1.开尔文表述：从单一热源吸取热量使它完全变为有用功的循环过程是不存在的〔热机效率为100是不可能的〕。2.克劳修斯表述：热量不能自动地从低温物体传到高温物体。两种表述是等价的.