- 2022-08-16 发布 |
- 37.5 KB |
- 33页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
大学物理大题及答案
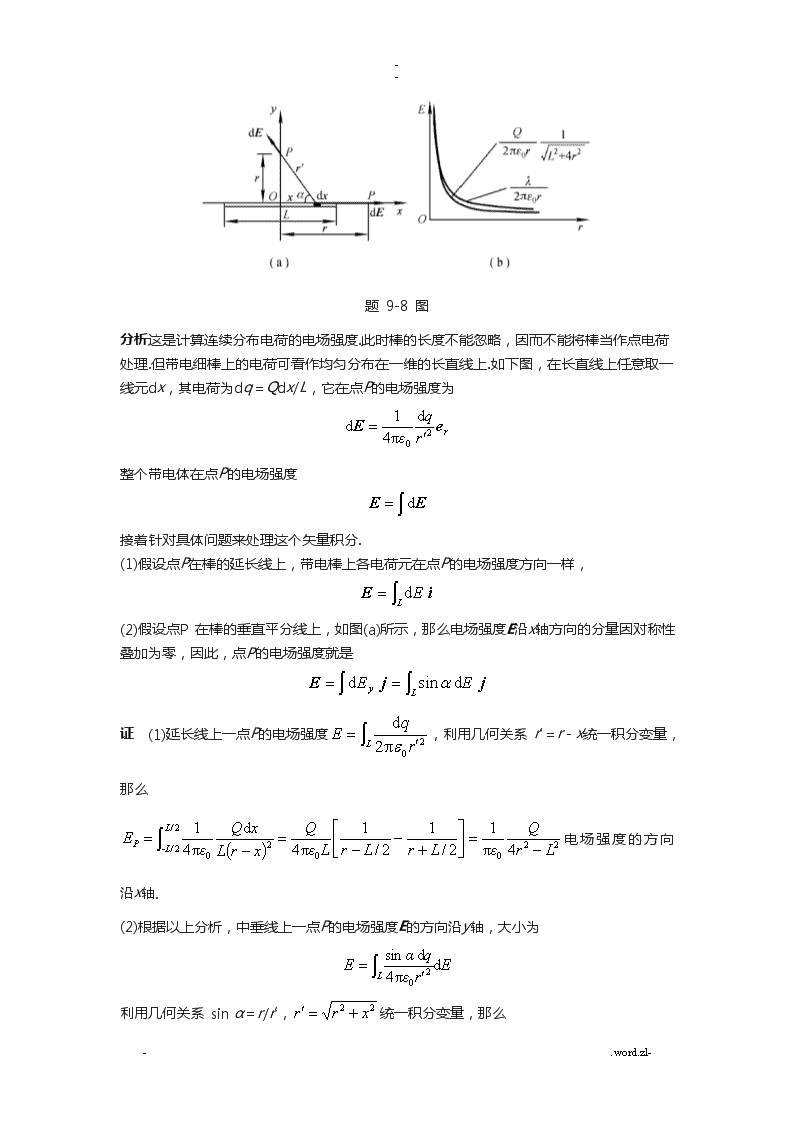
--容为:P37-7.8.14.15.19.21.25;P67-8.11.14.17;P123-11.14.15.17.19.21;P161-7.10.12.15;P236-9.10~14.16.18~23.27.28 第九章 静电场9-7点电荷如图分布,试求P点的电场强度.分析依照电场叠加原理,P点的电场强度等于各点电荷单独存在时在P点激发电场强度的矢量和.由于电荷量为q的一对点电荷在P点激发的电场强度大小相等、方向相反而相互抵消,P点的电场强度就等于电荷量为2.0q的点电荷在该点单独激发的场强度.解根据上述分析题9-7图9-8假设电荷Q均匀地分布在长为L的细棒上.求证:(1)在棒的延长线,且离棒中心为r处的电场强度为(2)在棒的垂直平分线上,离棒为r处的电场强度为假设棒为无限长(即L→∞),试将结果与无限长均匀带电直线的电场强度相比拟.-.word.zl-\n--题9-8图分析这是计算连续分布电荷的电场强度.此时棒的长度不能忽略,因而不能将棒当作点电荷处理.但带电细棒上的电荷可看作均匀分布在一维的长直线上.如下图,在长直线上任意取一线元dx,其电荷为dq=Qdx/L,它在点P的电场强度为整个带电体在点P的电场强度接着针对具体问题来处理这个矢量积分.(1)假设点P在棒的延长线上,带电棒上各电荷元在点P的电场强度方向一样,(2)假设点P在棒的垂直平分线上,如图(a)所示,那么电场强度E沿x轴方向的分量因对称性叠加为零,因此,点P的电场强度就是证 (1)延长线上一点P的电场强度,利用几何关系r′=r-x统一积分变量,那么电场强度的方向沿x轴.(2)根据以上分析,中垂线上一点P的电场强度E的方向沿y轴,大小为利用几何关系sinα=r/r′,统一积分变量,那么-.word.zl-\n--当棒长L→∞时,假设棒单位长度所带电荷λ为常量,那么P点电场强度此结果与无限长带电直线周围的电场强度分布一样[图(b)].这说明只要满足r2/L2<<1,带电长直细棒可视为无限长带电直线.9-14设在半径为R的球体电荷均匀分布,电荷体密度为,求带电球外的电场强度分布.分析电荷均匀分布在球体呈球对称,带电球激发的电场也呈球对称性.根据静电场是有源场,电场强度应该沿径向球对称分布.因此可以利用高斯定理求得均匀带电球外的电场分布.以带电球的球心为中心作同心球面为高斯面,依照高斯定理有上式中是高斯面的电荷量,分别求出处于带电球外的高斯面的电荷量,即可求得带电球外的电场强度分布.解依照上述分析,由高斯定理可得时,假设球体带正电荷,电场强度方向沿径向朝外.考虑到电场强度的方向,带电球体的电场强度为时,考虑到电场强度沿径向朝外,带电球体外的电场强度为-.word.zl-\n--9-15两个带有等量异号电荷的无限长同轴圆柱面,半径分别为R1和R2(R2>R1),单位长度上的电荷为λ.求离轴线为r处的电场强度:(1)r<R1,(2)R1<r<R2,(3)r>R2.题9-15图分析电荷分布在无限长同轴圆柱面上,电场强度也必定沿轴对称分布,取同轴圆柱面为高斯面,只有侧面的电场强度通量不为零,且,求出不同半径高斯面的电荷.即可解得各区域电场的分布.解作同轴圆柱面为高斯面,根据高斯定理r<R1, R1<r<R2,r>R2,在带电面附近,电场强度大小不连续,如图〔b〕所示,电场强度有一跃变9-19电荷面密度分别为+σ和-σ的两块“无限大〞均匀带电的平行平板,如图(a)放置,-.word.zl-\n--取坐标原点为零电势点,求空间各点的电势分布并画出电势随位置坐标x变化的关系曲线.题9-19图分析由于“无限大〞均匀带电的平行平板电荷分布在“无限〞空间,不能采用点电荷电势叠加的方法求电势分布:应该首先由“无限大〞均匀带电平板的电场强度叠加求电场强度的分布,然后依照电势的定义式求电势分布.解由“无限大〞均匀带电平板的电场强度,叠加求得电场强度的分布,电势等于移动单位正电荷到零电势点电场力所作的功电势变化曲线如图(b)所示.9-21一半径为R的无限长带电细棒,其部的电荷均匀分布,电荷的体密度为ρ.现取棒外表为零电势,求空间电势分布并画出分布曲线.-.word.zl-\n--题9-21图分析无限长均匀带电细棒电荷分布呈轴对称,其电场和电势的分布也呈轴对称.选取同轴柱面为高斯面,利用高斯定理可求得电场分布E(r),再根据电势差的定义并取棒外表为零电势(Vb=0),即可得空间任意点a的电势.解取高度为l、半径为r且与带电棒同轴的圆柱面为高斯面,由高斯定理当r≤R时得当r≥R时得取棒外表为零电势,空间电势的分布有当r≤R时当r≥R时如下图是电势V随空间位置r的分布曲线.-.word.zl-\n--9-25在一次典型的闪电中,两个放电点间的电势差约为109V,被迁移的电荷约为30C.(1)如果释放出来的能量都用来使0℃的冰融化成0℃的水,那么可溶解多少冰?(冰的融化热L=3.34×105J·kg)(2)假设每一个家庭一年消耗的能量为3000kW·h,那么可为多少个家庭提供一年的能量消耗?解 (1)假设闪电中释放出来的全部能量为冰所吸收,故可融化冰的质量即可融化约90吨冰.(2)一个家庭一年消耗的能量为一次闪电在极短的时间释放出来的能量约可维持3个家庭一年消耗的电能. 第十章 静电场中的导体与电介质10-8一导体球半径为R1,外罩一半径为R2的同心薄导体球壳,外球壳所带总电荷为Q,而球的电势为V0.求此系统的电势和电场的分布.分析假设,球电势等于外球壳的电势,那么外球壳必定为等势体,电场强度处处为零,球不带电.假设,球电势不等于外球壳电势,那么外球壳电场强度不为零,球带电.一般情况下,假设导体球带电q,导体到达静电平衡时电荷的分布如下图.依照电荷的这一分布,利用高斯定理可求得电场分布.并由或电势叠加求出电势的分布.最后将电场强度和电势用量V0、Q、R1、R2表示.-.word.zl-\n--题10-8图解根据静电平衡时电荷的分布,可知电场分布呈球对称.取同心球面为高斯面,由高斯定理,根据不同半径的高斯面的电荷分布,解得各区域的电场分布为r<R1时,R1<r<R2时,r>R2时,由电场强度与电势的积分关系,可得各相应区域的电势分布.r<R1时,R1<r<R2时, r>R2时, -.word.zl-\n--也可以从球面电势的叠加求电势的分布:在导体球〔r<R1〕在导体球和球壳之间〔R1<r<R2〕在球壳外〔r>R2〕为由题意得于是可求得各处的电场强度和电势的分布:r<R1时,;R1<r<R2时, ;r>R2时,-.word.zl-\n--;10-11电容式计算机键盘的每一个键下面连接一小块金属片,金属片与底板上的另一块金属片间保持一定空气间隙,构成一小电容器〔如图〕.当按下按键时电容发生变化,通过与之相连的电子线路向计算机发出该键相应的代码信号.假设金属片面积为50.0mm2,两金属片之间的距离是0.600mm.如果电路能检测出的电容变化量是0.250pF,试问按键需要按下多大的距离才能给出必要的信号?题10-11图分析按下按键时两金属片之间的距离变小,电容增大,由电容的变化量可以求得按键按下的最小距离:解按下按键时电容的变化量为按键按下的最小距离为-.word.zl-\n--10-14人体的某些细胞壁两侧带有等量的异号电荷.设某细胞壁厚为5.2×10-9m,两外表所带面电荷密度为±5.2×10-3C/m2,外表为正电荷.如果细胞壁物质的相对电容率为6.0,求〔1〕细胞壁的电场强度;〔2〕细胞壁两外表间的电势差.解 〔1〕细胞壁的电场强度;方向指向细胞外.〔2〕细胞壁两外表间的电势差.10-17 如图,有一个空气平板电容器,极板面积为S,间距为d.现将该电容器接在端电压为U的电源上充电,当〔1〕充足电后;〔2〕然后平行插入一块面积一样、厚度为δ〔δ<d〕、相对电容率为εr的电介质板;〔3〕将上述电介质换为同样大小的导体板.分别求电容器的电容C,极板上的电荷Q和极板间的电场强度E.题10-17图分析电源对电容器充电,电容器极板间的电势差等于电源端电压U.插入电介质后,由于介质界面出现极化电荷,极化电荷在介质中激发的电场与原电容器极板上自由电荷激发的电场方向相反,介质的电场减弱.由于极板间的距离d不变,因而与电源相接的导体极板将会从电源获得电荷,以维持电势差不变,并有相类似的原因,在平板电容器极板之间,假设平行地插入一块导体板,由于极板上的自由电荷和插入导体板上的感应电荷在导体板激发的电场相互抵消,与电源相接的导体极板将会从电源获得电荷,使间隙中的电场E增强,以维持两极板间的电势差不变,并有-.word.zl-\n--综上所述,接上电源的平板电容器,插入介质或导体后,极板上的自由电荷均会增加,而电势差保持不变.解 〔1〕空气平板电容器的电容充电后,极板上的电荷和极板间的电场强度为〔2〕插入电介质后,电容器的电容C1为故有介质电场强度空气中电场强度〔3〕插入导体到达静电平衡后,导体为等势体,其电容和极板上的电荷分别为-.word.zl-\n--导体中电场强度空气中电场强度无论是插入介质还是插入导体,由于电容器的导体极板与电源相连,在维持电势差不变的同时都从电源获得了电荷,自由电荷分布的变化同样使得介质的电场强度不再等于E0/εr.第十一章恒定磁场11-11如下图,几种载流导线在平面分布,电流均为I,它们在点O的磁感强度各为多少?题11-11图分析应用磁场叠加原理求解.将不同形状的载流导线分解成长直局部和圆弧局部,它们各自在点O处所激发的磁感强度较容易求得,那么总的磁感强度.解 〔a〕长直电流对点O而言,有,因此它在点O产生的磁场为零,那么点O处总的磁感强度为1/4圆弧电流所激发,故有B0的方向垂直纸面向外.〔b〕将载流导线看作圆电流和长直电流,由叠加原理可得B0的方向垂直纸面向里.-.word.zl-\n--〔c〕将载流导线看作1/2圆电流和两段半无限长直电流,由叠加原理可得B0的方向垂直纸面向外.11-1410mm2裸铜线允许通过50A电流而不会使导线过热.电流在导线横截面上均匀分布.求导线、外磁感强度的分布.题11-14图分析可将导线视作长直圆柱体,电流沿轴向均匀流过导体,故其磁场必然呈轴对称分布,即在与导线同轴的圆柱面上的各点,B大小相等、方向与电流成右手螺旋关系.为此,可利用安培环路定理,求出导线外表的磁感强度.解围绕轴线取同心圆为环路L,取其绕向与电流成右手螺旋关系,根据安培环路定理,有在导线r<R,,因而在导线外r>R,,因而磁感强度分布曲线如下图.11-15有一同轴电缆,其尺寸如图〔a〕所示.两导体中的电流均为I,但电流的流向相反,-.word.zl-\n--导体的磁性可不考虑.试计算以下各处的磁感强度:〔1〕r<R1;〔2〕R1<r<R2;〔3〕R2<r<R3;〔4〕r>R3.画出B-r图线.题11-15图分析同轴电缆导体的电流均匀分布,其磁场呈轴对称,取半径为r的同心圆为积分路径,,利用安培环路定理,可解得各区域的磁感强度.解由上述分析得r<R1R1<r<R2R2<r<R3r>R3-.word.zl-\n--磁感强度B〔r〕的分布曲线如图〔b〕.11-17电流I均匀地流过半径为R的圆形长直导线,试计算单位长度导线的磁场通过图中所示剖面的磁通量.题11-17图分析由题11-14可得导线部距轴线为r处的磁感强度在剖面上磁感强度分布不均匀,因此,需从磁通量的定义来求解.沿轴线方向在剖面上取面元dS=ldr,考虑到面元上各点B一样,故穿过面元的磁通量dΦ=BdS,通过积分,可得单位长度导线的磁通量解由分析可得单位长度导线的磁通量11-19霍尔效应可用来测量血流的速度,其原理如下图.在动脉血管两侧分别安装电极并加以磁场.设血管直径为d=2.0mm,磁场为B=0.080T,毫伏表测出血管上下两端的电压为UH=0.10mV,血流的流速为多大?-.word.zl-\n--题11-19图分析血流稳定时,有由上式可以解得血流的速度.解依照分析11-21从太阳射来的速度为0.80×108m/s的电子进入地球赤道上空高层艾伦辐射带中,该处磁场为4.0×10-7T,此电子回转轨道半径为多大?假设电子沿地球磁场的磁感线旋进到地磁北极附近,地磁北极附近磁场为2.0×10-5T,其轨道半径又为多少?解由带电粒子在磁场中运动的回转半径高层艾伦辐射带中的回转半径地磁北极附近的回转半径第十二章电磁感应电磁场和电磁波12-7载流长直导线中的电流以的变化率增长.假设有一边长为d的正方形线圈与导线处于同一平面,如下图.求线圈中的感应电动势.-.word.zl-\n--分析此题仍可用法拉第电磁感应定律,来求解.由于回路处在非均匀磁场中,磁通量就需用来计算.为了积分的需要,建立如下图的坐标系.由于B仅与x有关,即B=B(x),故取一个平行于长直导线的宽为dx、长为d的面元dS,如图中阴影局部所示,那么dS=ddx,所以,总磁通量可通过线积分求得〔假设取面元dS=dxdy,那么上述积分实际上为二重积分〕.此题在工程技术中又称为互感现象,也可用公式求解.解1穿过面元dS的磁通量为因此穿过线圈的磁通量为再由法拉第电磁感应定律,有解2当两长直导线有电流I通过时,穿过线圈的磁通量为线圈与两长直导线间的互感为当电流以变化时,线圈中的互感电动势为-.word.zl-\n--题12-7图12-10如图〔a〕所示,把一半径为R的半圆形导线OP置于磁感强度为B的均匀磁场中,当导线以速率v水平向右平动时,求导线中感应电动势E的大小,哪一端电势较高?题12-10图分析此题及后面几题中的电动势均为动生电动势,除仍可由求解外〔必须设法构造一个闭合回路〕,还可直接用公式求解.在用后一种方法求解时,应注意导体上任一导线元dl上的动生电动势.在一般情况下,上述各量可能是dl所在位置的函数.矢量〔v×B〕的方向就是导线中电势升高的方向.解1如图〔b〕所示,假想半圆形导线OP在宽为2R的静止形导轨上滑动,两者之间形成一个闭合回路.设顺时针方向为回路正向,任一时刻端点O或端点P距形导轨左侧距离为x,那么-.word.zl-\n--即由于静止的形导轨上的电动势为零,那么E=-2RvB.式中负号表示电动势的方向为逆时针,对OP段来说端点P的电势较高.解2建立如图〔c〕所示的坐标系,在导体上任意处取导体元dl,那么由矢量〔v×B〕的指向可知,端点P的电势较高.解3连接OP使导线构成一个闭合回路.由于磁场是均匀的,在任意时刻,穿过回路的磁通量常数.由法拉第电磁感应定律可知,E=0又因E=EOP+EPO即EOP=-EPO=2RvB由上述结果可知,在均匀磁场中,任意闭合导体回路平动所产生的动生电动势为零;而任意曲线形导体上的动生电动势就等于其两端所连直线形导体上的动生电动势.上述求解方法是叠加思想的逆运用,即补偿的方法12-12如下图,长为L的导体棒OP,处于均匀磁场中,并绕OO′轴以角速度ω旋转,棒与转轴间夹角恒为θ,磁感强度B与转轴平行.求OP棒在图示位置处的电动势.-.word.zl-\n--题12-12图分析如前所述,此题既可以用法拉第电磁感应定律计算〔此时必须构造一个包含OP导体在的闭合回路,如直角三角形导体回路OPQO〕,也可用来计算.由于对称性,导体OP旋转至任何位置时产生的电动势与图示位置是一样的.解1由上分析,得由矢量的方向可知端点P的电势较高.解2设想导体OP为直角三角形导体回路OPQO中的一局部,任一时刻穿过回路的磁通量Φ为零,那么回路的总电动势显然,EQO=0,所以由上可知,导体棒OP旋转时,在单位时间切割的磁感线数与导体棒QP等效.-.word.zl-\n--12-15在半径为R的圆柱形空间中存在着均匀磁场,B的方向与柱的轴线平行.如图〔a〕所示,有一长为l的金属棒放在磁场中,设B随时间的变化率为常量.试证:棒上感应电动势的大小为题12-15图分析变化磁场在其周围激发感生电场,把导体置于感生电场中,导体中的自由电子就会在电场力的作用下移动,在棒两端形成正负电荷的积累,从而产生感生电动势.由于此题的感生电场分布与上题所述情况完全一样,故可利用上题结果,由计算棒上感生电动势.此外,还可连接OP、OQ,设想PQOP构成一个闭合导体回路,用法拉第电磁感应定律求解,由于OP、OQ沿半径方向,与通过该处的感生电场强度Ek处处垂直,故,OP、OQ两段均无电动势,这样,由法拉第电磁感应定律求出的闭合回路的总电动势,就是导体棒PQ上的电动势.证1由电磁感应定律,在r<R区域,解得该区域感生电场强度的大小-.word.zl-\n--设PQ上线元dx处,Ek的方向如图〔b〕所示,那么金属杆PQ上的电动势为证2由法拉第电磁感应定律,有讨论假设金属棒PQ有一段在圆外,那么圆外一段导体上有无电动势?该如何求解?第十四章 波动光学14-9 在双缝干预实验中,用波长λ=546.1nm的单色光照射,双缝与屏的距离d′=300mm.测得中央明纹两侧的两个第五级明条纹的间距为12.2mm,求双缝间的距离.分析 双缝干预在屏上形成的条纹是上下对称且等间隔的.如果设两明纹间隔为Δx,那么由中央明纹两侧第五级明纹间距x5-x-5=10Δx可求出Δx.再由公式Δx=d′λ/d即可求出双缝间距d.解 根据分析:Δx=〔x5-x-5〕/10=1.22×10-3m双缝间距:d=d′λ/Δx=1.34×10-4m14-10 一个微波发射器置于岸上,离水面高度为d,对岸在离水面h高度处放置一接收器,水面宽度为D,且,如下图.发射器向对面发射波长为λ的微波,且λ>d,求接收器测到极大值时,至少离地多高?分析 由发射器直接发射的微波与经水面反射后的微波相遇可互相干预,这种干预与劳埃德镜实验完全一样.形成的干预结果与缝距为2d,缝屏间距为D-.word.zl-\n--的双缝干预相似,如图〔b〕所示,但要注意的是和劳埃德镜实验一样,由于从水面上反射的光存在半波损失,使得两束光在屏上相遇产生的光程差为,而不是.题14-10图解 由分析可知,接收到的信号为极大值时,应满足取k=1时,得.14-11如下图,将一折射率为1.58的云母片覆盖于氏双缝上的一条缝上,使得屏上原中央极大的所在点O改变为第五级明纹.假定=550nm,求:〔1〕条纹如何移动?〔2〕云母片的厚度t.题14-11图分析(1)此题是干预现象在工程测量中的一个具体应用,它可以用来测量透明介质薄片的微小厚度或折射率.在不加介质片之前,两相干光均在空气中传播,它们到达屏上任一点P的光程差由其几何路程差决定,对于点O,光程差Δ=0,故点O处为中央明纹,其余条纹相对点O-.word.zl-\n--对称分布.而在插入介质片后,虽然两相干光在两介质薄片中的几何路程一样,但光程却不同,对于点O,Δ≠0,故点O不再是中央明纹,整个条纹发生平移.原来中央明纹将出现在两束光到达屏上光程差Δ=0的位置.(2)干预条纹空间分布的变化完全取决于光程差的变化.因此,对于屏上某点P〔明纹或暗纹位置〕,只要计算出插入介质片前后光程差的变化,即可知道其干预条纹的变化情况.插入介质前的光程差Δ1=r1-r2=k1λ〔对应k1级明纹〕,插入介质后的光程差Δ2=〔n-1〕d+r1-r2=k1λ〔对应k1级明纹〕.光程差的变化量为Δ2-Δ1=〔n-1〕d=〔k2-k1〕λ式中〔k2-k1〕可以理解为移过点P的条纹数〔此题为5〕.因此,对于这类问题,求解光程差的变化量是解题的关键.解 由上述分析可知,两介质片插入前后,对于原中央明纹所在点O,有将有关数据代入可得14-12 白光垂直照射到空气中一厚度为380nm的肥皂膜上.设肥皂的折射率为1.32.试问该膜的正面呈现什么颜色?分析 这是薄膜干预问题,求正面呈现的颜色就是在反射光中求因干预增强光的波长〔在可见光围〕.解 根据分析对反射光加强,有-.word.zl-\n--在可见光围,k=2时,〔红光〕k=3时,〔紫光〕故正面呈红紫色.14-13 利用空气劈尖测细丝直径.如下图,λ=589.3nm,L=2.888×10-2m,测得30条条纹的总宽度为4.259×10-3m,求细丝直径d.分析 在应用劈尖干预公式时,应注意相邻条纹的间距b是N条条纹的宽度Δx除以〔N-1〕.对空气劈尖n=1.解 由分析知,相邻条纹间距,那么细丝直径为题14-13图14-14 集成光学中的楔形薄膜耦合器原理如下图.沉积在玻璃衬底上的是氧化钽〔〕薄膜,其楔形端从A到B厚度逐渐减小为零.为测定薄膜的厚度,用波长λ=632.8nm的激光垂直照射,观察到薄膜楔形端共出现11条暗纹,且A处对应一条暗纹,试求氧化钽薄膜的厚度.〔对632.8nm激光的折射率为2.21〕题14-14图分析 置于玻璃上的薄膜AB段形成劈尖,求薄膜厚度就是求该劈尖在A点处的厚度.由于-.word.zl-\n--对激光的折射率大于玻璃,故从该劈尖上外表反射的光有半波损失,而下外表没有,因而两反射光光程差为Δ=2ne+λ/2.由反射光暗纹公式2nek+λ/2=〔2k+1〕λ/2,k=0,1,2,3,…,可以求厚度ek.又因为AB中共有11条暗纹〔因半波损失B端也为暗纹〕,那么k取10即得薄膜厚度.解 根据分析,有2nek+=〔2k+1〕λ/2 〔k=0,1,2,3,…〕取k=10,得薄膜厚度e10==1.4×10-6m.14-16如图(a)所示的干预膨胀仪,样品的平均高度为3.0×10-2m,用λ=589.3nm的单色光垂直照射.当温度由17℃上升至30℃时,看到有20条条纹移过,问样品的热膨胀系数为多少?题14-16图分析 温度升高ΔT=T2-T1后,样品因受热膨胀,其高度l的增加量Δl=lαΔT.由于样品外表上移,使在倾角θ不变的情况下,样品与平板玻璃间的空气劈的整体厚度减小.根据等厚干预原理,干预条纹将整体向棱边平移,那么原k级条纹从a移至a′处,如图〔b〕所示,移过某一固定观察点的条纹数目N与Δl的关系为,由上述关系可得出热膨胀系数α.解 由题意知,移动的条纹数N=20,从分析可得-.word.zl-\n--那么热膨胀系数K14-18 如下图,折射率n2=1.2的油滴落在n3=1.50的平板玻璃上,形成一上外表近似于球面的油膜,测得油膜中心最高处的高度dm=1.1μm,用λ=600nm的单色光垂直照射油膜,求〔1〕油膜周边是暗环还是明环?〔2〕整个油膜可看到几个完整的暗环?题14-18图分析 此题也是一种牛顿环干预现象,由于n1<n2<n3,故油膜上任一点处两反射相干光的光程差Δ=2n2d.〔1〕令d=0,由干预加强或减弱条件即可判断油膜周边是明环.〔2〕由2n2d=〔2k+1〕λ/2,且令d=dm可求得油膜上暗环的最高级次〔取整〕,从而判断油膜上完整暗环的数目.解 〔1〕根据分析,由油膜周边处d=0,即Δ=0符合干预加强条件,故油膜周边是明环.〔2〕油膜上任一暗环处满足令d=dm,解得k=3.9,可知油膜上暗环的最高级次为3,故油膜上出现的完整暗环共有4个,即k=0,1,2,3.-.word.zl-\n--14-19 把折射率n=1.40的薄膜放入迈克耳干预仪的一臂,如果由此产生了7.0条条纹的移动,求膜厚.设入射光的波长为589nm.分析 迈克耳干预仪中的干预现象可以等效为薄膜干预〔两平面镜相互垂直〕和劈尖干预〔两平面镜不垂直〕两种情况,此题属于后一种情况.在干预仪一臂中插入介质片后,两束相干光的光程差改变了,相当于在观察者视野的空气劈尖的厚度改变了,从而引起干预条纹的移动.解 插入厚度为d的介质片后,两相干光光程差的改变量为2〔n-1〕d,从而引起N条条纹的移动,根据劈尖干预加强的条件,有2〔n-1〕d=Nλ,得14-20 如下图,狭缝的宽度b=0.60mm,透镜焦距f=0.40m,有一与狭缝平行的屏放置在透镜焦平面处.假设以波长为600nm的单色平行光垂直照射狭缝,那么在屏上离点O为x=1.4mm处的点P看到的是衍射明条纹.试求:〔1〕点P条纹的级数;〔2〕从点P看来对该光波而言,狭缝的波阵面可作半波带的数目.分析 单缝衍射中的明纹条件为,在观察点P位置确定〔即衍射角φ确定〕以及波长λ确定后,条纹的级数k也就确定了.而狭缝处的波阵面对明条纹可以划分的半波带数目为〔2k+1〕条.解 〔1〕设透镜到屏的距离为d,由于d>>b,对点P而言,有.根据分析中的条纹公式,有将b、d〔d≈f〕、x,λ的值代入,可得k=3-.word.zl-\n--〔2〕由分析可知,半波带数目为7.题14-20图14-21 一单色平行光垂直照射于一单缝,假设其第三条明纹位置正好和波长为600nm的单色光垂直入射时的第二级明纹的位置一样,求前一种单色光的波长.分析 采用比拟法来确定波长.对应于同一观察点,两次衍射的光程差一样,由于衍射明纹条件,故有,在两明纹级次和其中一种波长的情况下,即可求出另一种未知波长.解 根据分析,将代入,得14-22 单缝宽度b=1.0×10-4m,透镜焦距f=0.50m,用λ1=400nm和λ2=760nm的单色平行光分别垂直照射,求这两种光的第一级明纹离屏中心的距离,以及这两条明纹之间的距离.假设用每厘米刻有1000条刻线的光栅代替这个单缝,那么这两种单色光的第一级明纹分别距屏中心多远?这两条明纹之间的距离又是多少?分析 用含有两种不同波长的混合光照射单缝或光栅,每种波长可在屏上独立地产生自己的一组衍射条纹,屏上最终显示出两组衍射条纹的混合图样.因而此题可根据单缝〔或光栅〕衍射公式分别计算两种波长的k级条纹的位置x1和x2,并算出其条纹间距Δx=x2-x1-.word.zl-\n--.通过计算可以发现,使用光栅后,条纹将远离屏中心,条纹间距也变大,这是光栅的特点之一.解 〔1〕当光垂直照射单缝时,屏上第k级明纹的位置当λ1=400nm和k=1时, x1=3.0×10-3m当λ2=760nm和k=1时, x2=5.7×10-3m其条纹间距 Δx=x2-x1=2.7×10-3m〔2〕当光垂直照射光栅时,屏上第k级明纹的位置为而光栅常数当λ1=400nm和k=1时, x1=2.0×10-2m当λ2=760nm和k=1时, x2=3.8×10-2m其条纹间距 14-23 老鹰眼睛的瞳孔直径约为6mm,问其最多飞翔多高时可看清地面上身长为5cm的小鼠?设光在空气中的波长为600nm.分析 两物体能否被分辨,取决于两物对光学仪器通光孔〔包括鹰眼〕的角θ和光学仪器的最小分辨角θ0的关系.当θ≥θ0时能分辨,其中θ=θ0为恰能分辨.在此题中为一定值,这里D是鹰的瞳孔直径.而,其中L为小鼠的身长,h为老鹰飞翔的高度.恰好看清时θ=θ0.解由分析可知L/h=1.22λ/D,得飞翔高度h=LD/〔1.22λ〕=409.8m.14-27 测得一池静水的外表反射出来的太是线偏振光,求此时太阳处在地平线的多大仰角处?〔水的折射率为1.33〕-.word.zl-\n--题14-27图分析 设太〔自然光〕以入射角i入射到水面,那么所求仰角.当反射光起偏时,根据布儒斯特定律,有〔其中n1为空气的折射率,n2为水的折射率〕.解 根据以上分析,有那么14-28 一束光是自然光和线偏振光的混合,当它通过一偏振片时,发现透射光的强度取决于偏振片的取向,其强度可以变化5倍,求入射光中两种光的强度各占总入射光强度的几分之几.分析 偏振片的旋转,仅对入射的混合光中的线偏振光局部有影响,在偏振片旋转一周的过程中,当偏振光的振动方向平行于偏振片的偏振化方向时,透射光强最大;而相互垂直时,透射光强最小.分别计算最大透射光强Imax和最小透射光强Imin,按题意用相比的方法即能求解.解 设入射混合光强为I,其中线偏振光强为xI,自然光强为〔1-x〕I.按题意旋转偏振片,那么有最大透射光强最小透射光强-.word.zl-\n--按题意,那么有解得 x=2/3即线偏振光占总入射光强的2/3,自然光占1/3.-.word.zl-查看更多