大学物理下册复习
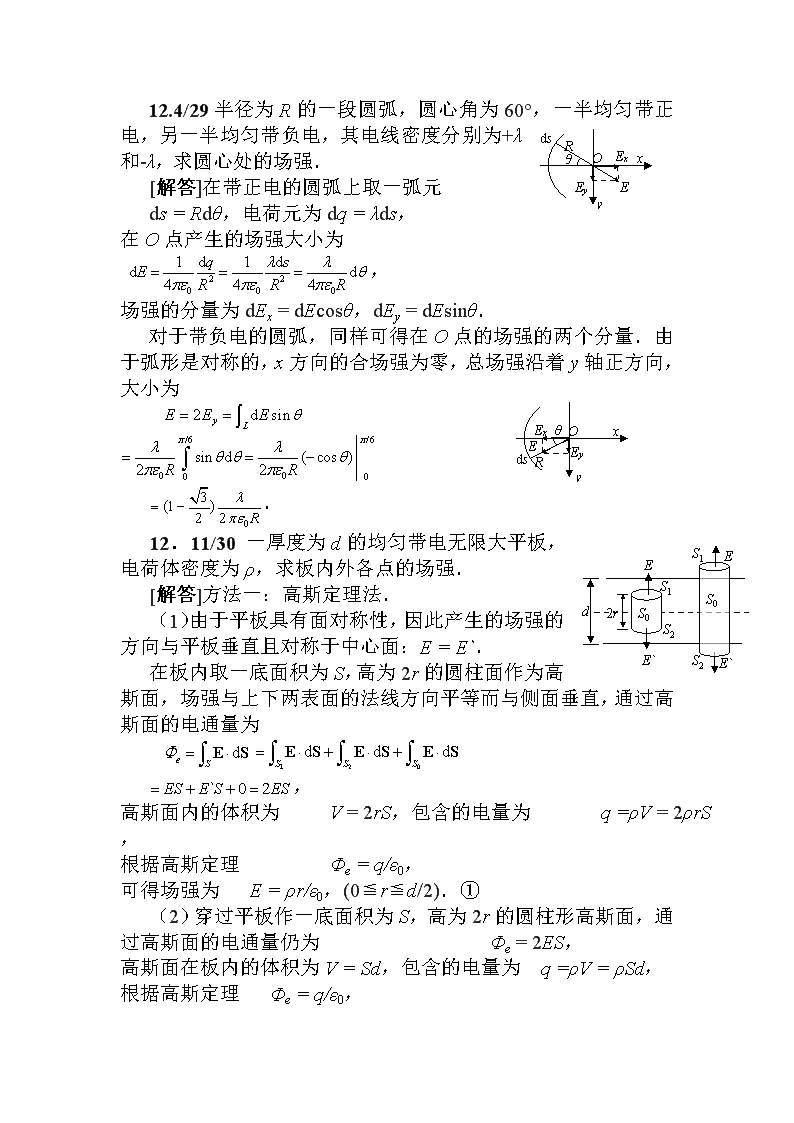
12.4/29半径为R的一段圆弧,圆心角为60°,一半均匀带正电,另一半均匀带负电,其电线密度分别ExxEθRdsEyOy为+λ和-λ,求圆心处的场强.[解答]在带正电的圆弧上取一弧元ds=Rdθ,电荷元为dq=λds,在O点产生的场强大小为,场强的分量为dEx=dEcosθ,dEy=dEsinθ.对于带负电的圆弧,同样可得在O点的场强的两个分量.由于弧形是对称的,x方向的合场强为零,总场强沿着y轴正方向,大小为dsExxEθREyOy.S2S1E`S1S2EEd2rS0E`S012.11/30一厚度为d的均匀带电无限大平板,电荷体密度为ρ,求板内外各点的场强.[解答]方法一:高斯定理法.(1)由于平板具有面对称性,因此产生的场强的方向与平板垂直且对称于中心面:E=E`.在板内取一底面积为S,高为2r的圆柱面作为高斯面,场强与上下两表面的法线方向平等而与侧面垂直,通过高斯面的电通量为,高斯面内的体积为V=2rS,包含的电量为q=ρV=2ρrS,根据高斯定理Φe=q/ε0,可得场强为E=ρr/ε0,(0≦r≦d/2).①(2)穿过平板作一底面积为S,高为2r的圆柱形高斯面,通过高斯面的电通量仍为Φe=2ES,高斯面在板内的体积为V=Sd,包含的电量为q=ρV=ρSd,根据高斯定理Φe=q/ε0,\n可得场强为E=ρd/2ε0,(r≧d/2).②方法二:场强迭加法.(1)由于平板的可视很多薄板迭而成的,以r为界,下面平板产生E2dyryoE1d的场强方向向上,上面平板产生的场强方向向下.在下面板中取一薄层dy,面电荷密度为dσ=ρdy,产生的场强为dE1=dσ/2ε0,积分得,③同理,上面板产生的场强为,④r处的总场强为E=E1-E2=ρr/ε0.(2)在公式③和④中,令r=d/2,得E2=0、E=E1=ρd/2ε0,E就是平板表面的场强.平板外的场强是无数个无限薄的带电平板产生的电场迭加的结果,是均强电场,方向与平板垂直,大小等于平板表面的场强,也能得出②式.12.15/30真空中有两块相互平行的无限大均匀带电平面A和B.A平面的电荷面密度为2σ,B平面的电荷面密度为σ,两面间的距离为d.当点电荷q从A面移到B面时,电场力做的功为多少?[解答]两平面产生的电场强度大小分别为EA=2σ/2ε0=σ/ε0,EB=σ/2ε0,两平面在它们之间产生的场强方向相反,因此,总场强大小为E=EA-EB=σ/2ε0,方向由A平面指向B平面.两平面间的电势差为U=Ed=σd/2ε0,当点电荷q从A面移到B面时,电场力做的功为W=qU=qσd/2ε0.BoAPrArCrB图13.113.1/56一带电量为q,半径为rA的金属球A,与一原先不带电、内外半径分别为rB和rC的金属球壳B同心放置,如图所示,则图中P点的电场强度如何?若用导线将A和B连接起来,则A球的电势为多少?(设无穷远处电势为零)\n[解答]过P点作一个同心球面作为高斯面,尽管金属球壳内侧会感应出异种,但是高斯面内只有电荷q.根据高斯定理可得E4πr2=q/ε0,可得P点的电场强度为.当金属球壳内侧会感应出异种电荷-q时,外侧将出现同种电荷q.用导线将A和B连接起来后,正负电荷将中和.A球是一个等势体,其电势等于球心的电势.A球的电势是球壳外侧的电荷产生的,这些电荷到球心的距离都是rc,所以A球的电势为13.3/56金属球壳原来带有电量Q,壳内外半径分别为a、b,壳内距球心qobar图13.3为r处有一点电荷q,求球心o的电势为多少?[解答]点电荷q在内壳上感应出负电荷-q,不论电荷如何分布,距离球心都为a.外壳上就有电荷q+Q,距离球为b.球心的电势是所有电荷产生的电势迭加,大小为13.10/58圆柱形电容器是由半径为R1的导线和与它同轴的内半径为R2的导体圆筒构成的,其长为l,其间充满了介电常量为ε的介质.设沿轴线单位长度导线上的电荷为λ,圆筒的电荷为-λ,略去边缘效DS1S2S0rR2R1εl应.求:(1)两极的电势差U;(2)介质中的电场强度E、电位移D;(3)电容C,它是真空时电容的多少倍?[解答]介质中的电场强度和电位移是轴对称分布的.在内外半径之间作一个半径为r、长为l的圆柱形高斯面,侧面为S0,上下两底面分别为S1和S2.通过高斯面的电位移通量为,高斯面包围的自由电荷为q=λl,根据介质中的高斯定理Φd=q,可得电位为D=λ/2πr,方向垂直中心轴向外.\n电场强度为E=D/ε=λ/2πεr,方向也垂直中心轴向外.取一条电力线为积分路径,电势差为.电容为.在真空时的电容为,所以倍数为C/C0=ε/ε0.13.14一平行板电容器板面积为S,板间距离为d,两板竖直放着.若电容器两板充电到电压为U时,断开电源,使电容器的一半浸在相对介电常量为εr的液体中.求:(1)电容器的电容C;(2)浸入液体后电容器的静电能;(3)极板上的自由电荷面密度.[解答](1)如前所述,两电容器并联的电容为C=(1+εr)ε0S/2d.(2)电容器充电前的电容为C0=ε0S/d,充电后所带电量为Q=C0U.当电容器的一半浸在介质中后,电容虽然改变了,但是电量不变,所以静电能为W=Q2/2C=C02U2/2C=ε0SU2/(1+εr)d.(3)电容器的一半浸入介质后,真空的一半的电容为C1=ε0S/2d;介质中的一半的电容为C2=ε0εrS/2d.设两半的所带自由电荷分别为Q1和Q2,则Q1+Q2=Q.①由于C=Q/U,所以U=Q1/C1=Q2/C2.②解联立方程得,真空中一半电容器的自由电荷面密度为.同理,介质中一半电容器的自由电荷面密度为.\n13.17/58两个同轴的圆柱面,长度均为l,半径分别为a、b,柱面之间充满介电常量为ε的电介质(忽略边缘效应).当这两个导体带有等量异号电荷(±Q)时,求:(1)在半径为r(a
>b,求B0与pm.[解答](1)直线转动的周期为T=2π/ω,在直线上距O为r处取一径向线元dr,所带的电量为dq=λdr,形成的圆电流元为dI=dq/T=ωλdr/2π,在圆心O点产生的磁感应强度为dB=μ0dI/2r=μ0ωλdr/4πr,整个直线在O点产生磁感应强度为,\n如果λ>0,B的方向垂直纸面向外.(2)圆电流元包含的面积为S=πr2,形成的磁矩为dpm=SdI=ωλr2dr/2,积分得.如果λ>0,pm的方向垂直纸面向外.(3)当a>>b时,因为,所以..14.20/99一圆线圈直径为8cm,共12匝,通有电流5A,将此线圈置于磁感应强度为0.6T的均强磁场中,求:(1)作用在线圈上的电大磁力矩为多少?(2)线圈平面在什么位置时磁力矩为最大磁力矩的一半.[解答](1)线圈半径为R=0.04m,面积为S=πR2,磁矩为pm=NIS=πR2NI,磁力矩为M=pmBsinθ.当θ=π/2时,磁力矩最大Mm=pmB=πR2NIB=0.18(N·m).(2)由于M=Mmsinθ,当M=Mm/2时,可得sinθ=0.5,θ=30°或150°.15.3/112一螺绕环中心周长l=10cm,线圈匝数N=200匝,线圈中通有电流I=100mA.求:(1)管内磁感应强度B0和磁场强度H0为多少?(2)设管内充满相对磁导率μr=4200的铁磁质,管内的B和H是多少?(3)磁介质内部由传导电流产生的B0和由磁化电流产生的B`各是多少?[解答](1)管内的磁场强度为=200(A·m-1).磁感应强度为B=μ0H0=4π×10-7×200=2.5×10-4(T).(2)当管内充满铁磁质之后,磁场强度不变H=H0=200(A·m-1).\n磁感应强度为B=μH=μrμ0H=4200×4π×10-7×200=1.056(T).(3)由传导电流产生的B0为2.5×10-4T.由于B=B0+B`,所以磁化电流产生的磁感应强度为B`=B-B0≈1.056(T).16.1/145一条铜棒长为L=0.5m,水平放置,可绕距离A端为L/5处和棒垂直的轴OO`在水平面内旋转,每秒转动一周.铜棒置于竖直向上的匀强磁场中,如图所示,磁感应强度B=1.0×10-4T.求铜棒两端A、B的电势差,何端电势高.[解答]设想一个半径为R的金属棒绕一端做匀速圆周运动,角速度为ω,经过时间dt后转过的角度为dθ=ωdt,OO`BABL/5ω图16.1扫过的面积为dS=R2dθ/2,切割的磁通量为dΦ=BdS=BR2dθ/2,动生电动势的大小为ε=dΦ/dt=ωBR2/2.根据右手螺旋法则,圆周上端点的电势高.AO和BO段的动生电动势大小分别为dθLωoRl,.由于BO>AO,所以B端的电势比A端更高,A和B端的电势差为=4.71×10-4(V).[讨论]如果棒上两点到o的距离分别为L和l,则两点间的电势差为.16.6/146如图,有一弯成θ角的金属架COD放在磁场中,磁感应强度B的方向垂直于金属架COD所在平面,一导体杆MN垂直于OD边,并在金属架上以恒定速度v向右滑动,v与MN垂直,设t=0时,x=0,求下列两情形,框架内的感应电动势εi.BMNOvCDxθ图16.6(1)磁场分布均匀,且B不随时间改变;(2)非均匀的交变磁场B=Kxcosωt.[解答](1)经过时间t,导体杆前进的距离为x=vt,\n杆的有效长度为l=xtanθ=v(tanθ)t,动生电动势为εi=Blv=Bv2(tanθ)t.(2)导体杆扫过的三角形的面积为S=xl/2=x2tanθ/2=v2t2tanθ/2,通过该面的磁通量为感应电动势为,即:.16.7/146如图所示的回路,磁感应强度B垂直于回路平面向里,磁通量按下述规律变化Φ=3t2+2t+1,式中Φ的单位为毫韦伯,t的单位为秒.求:BR图16.7(1)在t=2s时回路中的感生电动势为多少?(2)电阻上的电流方向如何?[解答](1)将磁通量的单位化为韦伯得Φ=(3t2+2t+1)/103,感生电动势大小为ε=|dΦ/dt|=2(3t+1)/103.t=2s时的感生电动势为1.4×10-2(V).(2)由于原磁场在增加,根据楞次定律,感应电流所产生的磁场的方向与原磁场的方向相反,所以在线圈中感生电流的方向是逆时针的,从电阻的左边流向右边.16.9/146如图所示,匀强磁场B与矩形导线回路的法线n成θ=60°角,B=kt(k为大于零的常数).长BAθLDBnv图16.9为L的导体杆AB以匀速v向右平动,求回路中t时刻的感应电动势的大小和方向(设t=0时,x=0).[解答]经过时间t,导体杆运动的距离为x=vt,扫过的面积为S=Lx=Lvt,通过此面积的磁通量为Φ=B·S=BScosθ=Lvkt2/2.感应电动势的大小为ε=dΦ/dt=Lvkt.\n由于回路中磁通量在增加,而感应电流的磁通量阻碍原磁通量增加,其磁场与原磁场的方向相反,所以感应电动势的方向是顺时针的.16.10/147长为b,宽为a的矩形线圈ABCD与无限长直截流导线共面,且线圈的长边平行于长直导线,线圈以速度v向右平动,t时刻基AD边距离长直导线为x;且长直导线中的电流按I=I0cosωt规律随时BABvDCxrxdrxbxa图16.10间变化,如图所示.求回路中的电动势ε.[解答]电流I在r处产生的磁感应强度为,穿过面积元dS=bdr的磁通量为,穿过矩形线圈ABCD的磁通量为,回路中的电动势为.显然,第一项是由于磁场变化产生的感生电动势,第二项是由于线圈运动产生的动生电动势.16.17/148长直导线与矩形单匝线圈共面放置,导线与线圈的长边平行,矩形线圈的边长分别为a、b,它到直导线的距离为c(如图),当矩形线圈中通有电流I=I0sinωt时,Ibca图16.17求直导线中的感应电动势.[解答]如果在直导线中通以稳恒电流I,在距离为r处产生的磁感应强度为B=μ0I/2πr.在矩形线圈中取一面积元dS=bdr,通过线圈的磁通量为,互感系数为.当线圈中通以交变电流I=I0sinωt\n时,直导线中的感应电动势大小为.16.19两个线圈的自感分别为L1和L2,,它们之间的互感为M.将两个线圈顺串联,如图a所示,求1和4之间的互感;(2)将两线圈反串联,如图b所示,求1和3之间的自感.[解答]两个线圈串联时,通以电流I之后,总磁场等于两个线圈分别产生的磁场的向量和B=B1+B2,磁场的能量为.(1)当两个线圈顺串时,两磁场的方向相同,θ=0,所以,自感系数为.(2)当两个线圈反串时,两磁场的方向相反,θ=π,所以,自感系数为.16.21/149一螺绕环中心轴线的周长L=500mm,横截面为正方形,其边长为bboo`bI图16.21=15mm,由N=2500匝的绝缘导线均匀密绕面成,铁芯的相对磁导率μr=1000,当导线中通有电流I=2.0A时,求:(1)环内中心轴在线处的磁能密度;(2)螺绕环的总磁能.[解答](1)设螺绕环单位长度上的线圈匝数为n=N/L,中心的磁感应强度为B=μnI,其中μ=μrμ0.磁场强度为H=B/μ=nI,因此中心轴在线能量密度为=2π×104(J·m-3).(2)螺绕环的总体积约为V=b2L,将磁场当作匀强磁场,总磁能为W=wV=2π×104×(0.015)2×0.5=2.25π=7.07(J).\n16.25/149一平行板电容器的两极板面积为S的圆形金属板,接在交流电源上,板上电荷随时间变化,q=qmsinωt.求:(1)电容器中的位移电流密度;(2)两极板间磁感应强度的分布.[解答](1)平行板电容器的面电荷密度为σ=q/S,位移电流密度为.(2)在安培-麦克斯韦环路定律中,两极板间没有传导电流,即I=0.由于轴对称,在两板之间以轴为圆心作一个半径为r的圆,其周长为C=2πr,使磁场的方向与环路的方向相同,左边为.环路所包围的面积为S`=πr2,右边的位移电流为.因此,两极板间磁场强度的分布为,磁感应强度的分布为.