- 2022-08-16 发布 |
- 37.5 KB |
- 6页
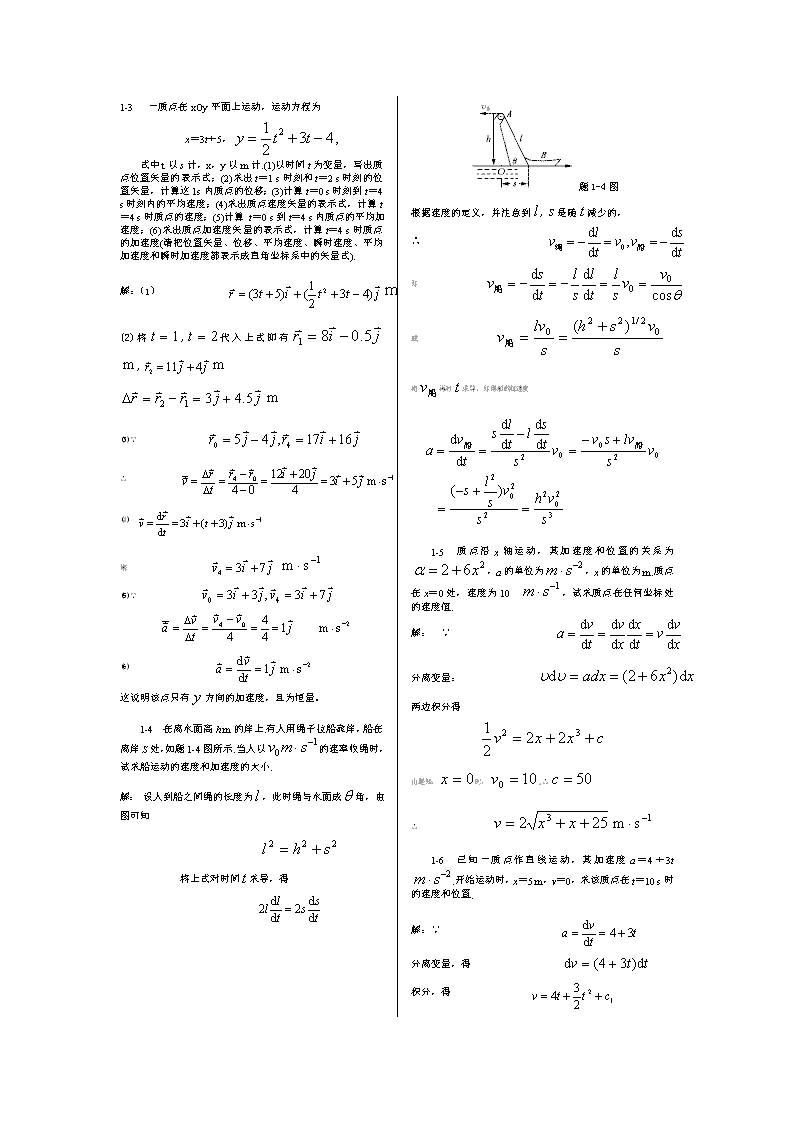


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
大学物理答案11450
1-3 一质点在xOy平面上运动,运动方程为x=3t+5,,式中t以s计,x,y以m计.(1)以时间t为变量,写出质点位置矢量的表示式;(2)求出t=1s时刻和t=2s时刻的位置矢量,计算这1s内质点的位移;(3)计算t=0s时刻到t=4s时刻内的平均速度;(4)求出质点速度矢量的表示式,计算t=4s时质点的速度;(5)计算t=0s到t=4s内质点的平均加速度;(6)求出质点加速度矢量的表示式,计算t=4s时质点的加速度(请把位置矢量、位移、平均速度、瞬时速度、平均加速度和瞬时加速度都表示成直角坐标系中的矢量式).解:(1)(2)将,代入上式即有,(3)∵∴(4)则(5)∵(6)这说明该点只有方向的加速度,且为恒量。1-4 在离水面高hm的岸上.有人用绳子拉船靠岸,船在离岸S处,如题1-4图所示.当人以的速率收绳时,试求船运动的速度和加速度的大小.解:设人到船之间绳的长度为,此时绳与水面成角,由图可知 将上式对时间求导,得题1-4图根据速度的定义,并注意到,是随减少的,∴即或将再对求导,即得船的加速度1-5 质点沿x轴运动,其加速度和位置的关系为,a的单位为,x的单位为m.质点在x=0处,速度为10,试求质点在任何坐标处的速度值.解:∵分离变量:两边积分得由题知,时,,∴∴1-6 已知一质点作直线运动,其加速度a=4+3t.开始运动时,x=5m,v=0,求该质点在t=10s时的速度和位置.解:∵分离变量,得积分,得\n由题知,,,∴故又因为分离变量,积分得由题知,,∴故所以时1-7 一质点沿半径为1m的圆周运动,运动方程为,式中θ以rad计,t以s计,求:(1)t=2s时,质点的切向加速度和法向加速度;(2)当加速度的方向和半径成45°角时,其角位移是多少?解:(1)时,(2)当加速度方向与半径成角时,有即亦即则解得于是角位移为2-2 质量为16kg的质点在xOy平面内运动,受一恒力作用,力的分量为fx=6N,fy=-7N.当t=0时,x=y=0,vx=-2m·s-1,vy=0.求当t=2s时质点的位矢和速度.解:(1)于是质点在时的速度(2)2-3 质点在流体中作直线运动,受与速度成正比的阻力kv(k为常数)作用,t=0时质点的速度为v0.证明:(1)t时刻的速度为;(2)由0到t的时间内经过的距离为;(3)停止运动前经过的距离为;(4)证明当时速度减至v0的,式中m为质点的质量.答:(1)∵分离变量,得即∴(2)(3)质点停止运动时速度为零,即t→∞,\n故有(4)当t=时,其速度为即速度减至的.2-7 设F=7i-6jN.(1)当一质点从原点运动到r=-3i+4j+16km时,求F所做的功;(2)如果质点到r处时需0.6s,试求平均功率;(3)如果质点的质量为1kg,试求动能的变化.解:(1)由题知,为恒力,∴(2)(3)由动能定理,题5-2图5-2 两小球的质量都是m,都用长为l的细绳挂在同一点,它们带有相同电量,静止时两线夹角为2θ,如题5--2图所示.设小球的半径和线的质量都可以忽略不计,求每个小球所带的电量.解:如题5-2图示解得5-4 长l=15.0cm的直导线AB上均匀地分布着线密度的正电荷.试求:(1)在导线的延长线上与导线B端相距处P点的场强;(2)在导线的垂直平分线上与导线中点相距处Q点的场强.解:如题5-4图所示(1)在带电直线上取线元,其上电量在点产生场强为用,,代入得方向水平向右(2)同理方向如题5-4图所示由于对称性,即只有分量,∵以,,代入得,方向沿轴正向5-5 (1)点电荷q位于一边长为a的立方体中心,试求在该点电荷电场中穿过立方体的一个面的电通量;(2)如果该场源点电荷移动到该立方体的一个顶点上,这时穿过立方体各面的电通量是多少?解:(1)由高斯定理立方体六个面,当在立方体中心时,每个面上电通量相等∴各面电通量.(2)电荷在顶点时,将立方体延伸为边长的立方体,使处于边长的立方体中心,则边长的正方形上电通量\n对于边长的正方形,如果它不包含所在的顶点,则, 如果它包含所在顶点则.5-9 如题5-9图所示,在A,B两点处放有电量分别为+q,-q的点电荷,AB间距离为2R,现将另一正试验点电荷从O点经过半圆弧移到C点,求移动过程中电场力做的功.解:如题5-9图示∴6-4 如题6-4图所示,AB、CD为长直导线,BC为圆心在O点的一段圆弧形导线,其半径为R.若通以电流I,求O点的磁感应强度.解:如题6-4图所示,点磁场由、、三部分电流产生.其中产生产生,方向垂直向里段产生,方向向里∴,方向向里.6-8 一根很长的同轴电缆,由一导体圆柱(半径为a)和一同轴的导体圆管(内、外半径分别为b,c)构成,如题6-8图所示.使用时,电流I从一导体流去,从另一导体流回.设电流都是均匀地分布在导体的横截面上,求:(1)导体圆柱内(),(2)两导体之间(),(3)导体圆筒内(),(4)电缆外()各点处磁感应强度的大小.解:(1)(2)(3)(4)6-13 电子在的匀强磁场中作圆周运动,圆周半径r=3.0cm.已知垂直于纸面向外,某时刻电子在A点,速度v向上,如题6-13图所示.(1)试画出这电子运动的轨道;(2)求这电子速度v的大小;(3)求这电子的动能.解:(1)轨迹如图题6-13图(2)∵∴(3)\n7-3 如题7-3图所示,在两平行载流的无限长直导线的平面内有一矩形线圈.两导线中的电流方向相反、大小相等,且电流以的变化率增大,求:(1)任一时刻线圈内所通过的磁通量;(2)线圈中的感应电动势.解:以向外磁通为正则(1)(2)7-5 长度为l的金属杆ab以速率v在导电轨道abcd上平行移动.已知导轨处于均匀磁场B中,B的方向与回路的法线成60°角(如题7-5图所示),B的大小为B=kt(k为正常数).设t=0时杆位于cd处,求:任一时刻t导线回路中感应电动势的大小和方向.题7-5图解:∴即沿方向顺时针方向.7-7 导线ab长为l,绕过O点的垂直轴以匀角速ω转动.,磁感应强度B平行于转轴,如题7-7所示.试求:(1)ab两端的电势差;(2)a,b两端哪一点电势高?题7-7图解:(1)在上取一小段则同理∴(2)∵即∴点电势高.10-1 在杨氏双缝实验中,作如下调节时,屏幕上的干涉条纹将如何变化?试说明理由.(1)使两缝之间的距离变小;(2)保持双缝间距不变,使双缝与屏幕间的距离变小;(3)整个装置的结构不变,全部浸入水中;(4)光源作平行于S1,S2联线方向上下微小移动;解:由知,(1)条纹变疏;(2)条纹变密;(3)条纹变密;(4)零级明纹在屏幕上作相反方向的上下移动;10-4 在杨氏双缝实验中,双缝间距d=0.20mm,缝屏间距D=1.0m.试求:(1)若第2级明条纹离屏中心的距离为6.0mm,计算此单色光的波长;(2)求相邻两明条纹间的距离.解:(1)由知,,∴(2)10-16 使自然光通过两个偏振化方向夹角为60°的偏振片时,透射光强为I1,今在这两个偏振片之间再插入一偏振片,它的偏振化方向与前两个偏振片均成30°,问此时透射光强I与I1之比为多少?解:由马吕斯定律\n∴10-17 一束自然光从空气入射到折射率为1.40的液体表面上,其反射光是完全偏振光.试求:(1)入射角等于多少?(2)折射角为多少?解:(1)∴(2)10-18 利用布儒斯特定律怎样测定不透明介质的折射率?若测得釉质在空气中的起偏振角为58°,求釉质的折射率.解:由,故查看更多