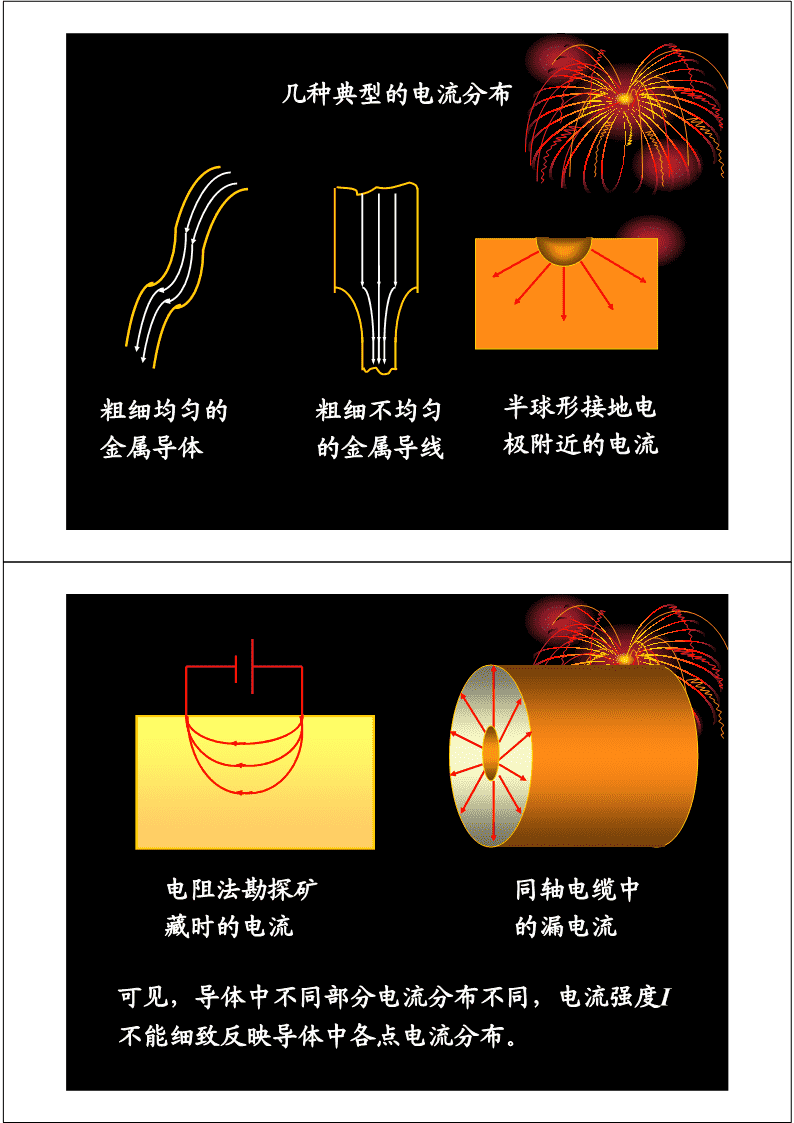
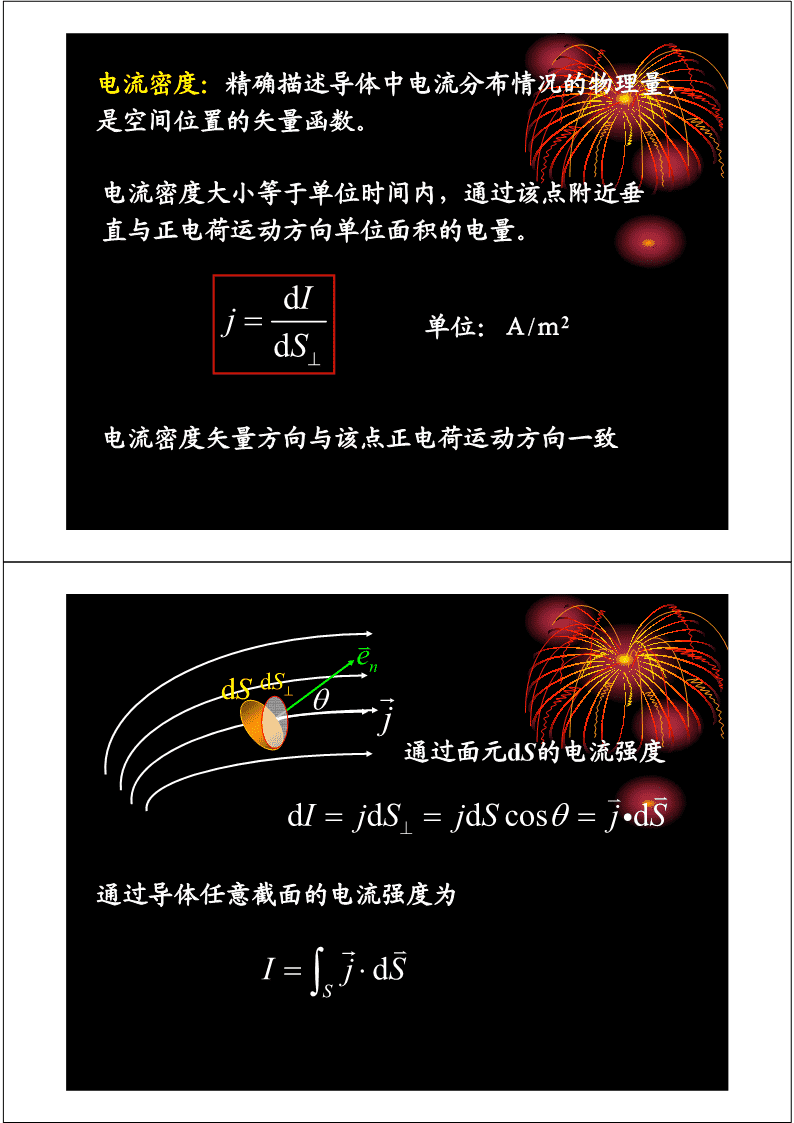
大学物理下new
§10-1电流密度电动势一、电流强度和电流密度一、电流强度和电流密度传导电流:自由电荷的定向运动。方向:正电荷的移动方向,与电子的运动方向相反。电流强度:单位时间通过导体某一横截面的电量。dqI=dt36单位:安培(A)1A10mA10A==μ恒定电流:电流强度的大小和方向不随时间而变化。\n几种典型的电流分布粗细均匀的粗细不均匀半球形接地电金属导体的金属导线极附近的电流电阻法勘探矿同轴电缆中藏时的电流的漏电流可见,导体中不同部分电流分布不同,电流强度I不能细致反映导体中各点电流分布。\n电流密度:精确描述导体中电流分布情况的物理量,是空间位置的矢量函数。电流密度大小等于单位时间内,通过该点附近垂直与正电荷运动方向单位面积的电量。dIj=单位:A/m2dS⊥电流密度矢量方向与该点正电荷运动方向一致KendSdS⊥θGj通过面元dS的电流强度KKdddI==jSjScosdθ=jSi⊥通过导体任意截面的电流强度为GKI=⋅∫jSdS\n二、电源电动势二、电源电动势GE非静电力:能不断分离正负电荷使正电荷逆静电场力方向运动.+−+−−+−电源:提供非静电力的装置,+−+−非静电力作功把其他形式的能A电源B量转变成电势能。作用:在电源内部,“非静电力”作功,把电荷从电势能低的一端移到电势能高的一端,通过内部电荷的移动,保持外电路电场E存在。\nGE为了描述电源内非静电力移动电荷做功的本领,引入电动势的物理量,定义为单位正电荷绕闭合回路+−+−−运动一周,非静电力所做的功。+KE−+kKK−WF⋅dl+−v∫kε==A电源Bqq在电源内部,“非静电力”作功,可以设想在电源内部存在一“非静电场”,单位正电荷受到的非静电力定义KG为“非静电场的场强”记做Ekk=Fq。KKKKWFlq⋅⋅ddElKKv∫∫kkvε====⋅Eldv∫kqqqKKKKKKA+ε=⋅=⋅=⋅ElElEldddv∫∫∫kkkB−电源电动势大小等于将单位正电荷从负极经电源内部移至正极时非静电力所作的功。G反映电源作功能力,与外电路无关E电源电动势是有方向标量,规定+−其方向为电源内部负极指向正极+−−+KE−+k−单位:J/C,即V+−A电源B\n§10-2法拉第电磁感应定律一、电磁感应现象一、电磁感应现象电流能产生磁场(电流的磁效应)。反之,能否通过磁场产生电流?1831年英国科学家法拉第通过大量实验证实变化的磁场可以在导体内产生电动势(感应电动势)和电流(感应电流)。称为电磁感应现象。NSBAA图1图2实验现象:1、图1中电键闭合和打开瞬间,线圈A中有电流,但两种情况下电流的流向相反。2、图2中线圈与磁铁发生相对运动时,线圈A中有电流,电流的流向与相对运动情况有关。\n\n结论:当穿过一个闭合导体回路所包围的面积内的磁通量发生变化时(不论这种变化是由什么原因引起的),在导体回路中就有电流产生。这种现象称为电磁感应现象。回路中所产生的电流称为感应电流。相应的电动势则称为感应电动势。思考:在无限长直载流导线旁有相同大小的四个矩形线圈,分别作如图所示的运动。判断回路中是否有感应电流。ωIKKv⊗vKv(a)(b)(c)(d)ε≠0ε≠0ε=0ε≠0\n二、法拉第电磁感应定律楞次定律二、法拉第电磁感应定律楞次定律电磁感应定律的基本表述:通过回路所包围面积的磁通量发生变化时,回路中产生的感应电动势与磁通量对时间的变化率成正比.dΦmε=−kidtk为比例系数,式中各量取国际单位制时,则k=1dΦmε=−idt式中负号反映电动势的方向dΦmε=−idt式中εi和Φm都是标量,其正负由选择的正方向来定,相同为正,相反为负。先选定一个绕行方向电动势为正表示其方向与选定的绕行方向一致;电动势为负表示其方向与选定的绕行方向相反。\n有了选定的绕行方向,利用右手螺旋可以确定它的法K线方向nGnKK若B与n的夹角为锐角,则Φ取正值;mKK若B与n的夹角为钝角,则Φm取负值。dΦm有了Φm的正负,其变化率的正负就有了确定的dt意义。若正的Φ随时间增大,或负的Φ随时间减小,则mmdΦd0Φ>>,0mmdt若正的Φ随时间减小,或负的Φ随时间增大,则mmdΦd0Φ<,0m
0LΦ>0εiΦ↑εiΦ↓dΦ>0ε<0逆绕向dΦ<0ε>0顺绕向dtidtidΦε=−GidtGnnGG钝角B钝角BΦ<0Φ<0LLεiΦεiΦ↓↑dΦdΦdt<0εi>0顺绕向>0εi<0逆绕向dt6例题:一长直导线中通有交变电流I=Itsinω,在0长直导线旁平行放置一矩形线圈,线圈平面与直导线在同一平面内。已知线圈长为l,宽为l,线圈近长直12导线的一边离直导线距离为h。求任一瞬时线圈中的感应电动势εihl2GGμIbcdddΦ=BSi=0lx解:m12πxIhl+2l1μIΦ=Φd=0lxdmm∫∫12πxhadμ001Ilhl+2xdx=lnsinωt2πhdΦμIlhl+ε=−m=−001ln2cosωtidt2πh\n楞次定律:闭合回路中产生的感应电流具有确定的方向,它总是使感应电流所产生的通过回路面积的磁通量,去补偿或者反抗引起感应电流的磁通量的变化。楞次应用楞次定律判断感应电流的方向与法拉第定律是一致的。GGBBΦ↑Φ↓LLεεiiGGBΦ↑↓BΦLLεεii\n*例题:矩形框导体的一边ab可以平行滑动,长为l。整个矩形回路放在磁感强度为B、方向与其平面垂直的均匀磁场中。若导线ab以恒定的速率v向右运动,求闭合回路的感应电动势。a××d××××××××××××××GG×××B×××××v××××××××××××××××xo×××××××b×解:以固定边的位置为坐标原点,向右为x轴正方向。设t时刻ab边的坐标为x,取顺时针方向为bodab回路的绕行正方向,则该时刻穿过回路的磁通量为:Φ==BSBlxm选择顺时针为绕行正方向,Φm>0,当导线匀速向右dΦΦd0Φ>>,0m移动时正的m随时间增大,则mdtdΦdxm回路的感应电动势为:ε=−=−BlB=−lviddtt负号表示感应电动势的方向与回路的正方向相反,即沿回路的逆时针方向。也可不选定回路绕行方向,而是根据楞次定律判断感dΦ应电动势的方向,再由m算出感应电动势的大小。dt\n对N匝密绕线圈,由于匝与匝之间是串联的,整个线圈的电动势等于各匝所产生电动势之和。dΦdΨε=−N=−idtdt式中Ψ=NΦ磁通匝链数或全磁通,表示通过N匝线圈的总磁总量。§10-3动生电动势和感生电动势由法拉第电磁感应定律可以知道,只要通过回路所围面积中的磁通量发生变化,回路中就会产生感应电动势。引起磁通量变化的原因1)稳恒磁场中的导体运动,或者回路面积变化、取向变化等动生电动势2)导体不动,磁场变化感生电动势\n一、动生电动势一、动生电动势动生电动势可以看成是洛仑兹力引起的当导体以速度v向右运动时,导体内的自由电子也以速度v跟随它向右运动,自由电子受到的洛仑兹力为:KKKfm=−evB()×a+++++++++K式中-e为电子所带的电量,f的方B向由a到b,在洛仑兹力的推动下,++++Kv自由电子由a到b,b为负极,a为+++G+f正极。m++++b作用在电子上的洛仑兹力是一种非静电力GGfGGm定义非静电场Ek==vB×−eG||sEvk=BinθGG方向:vB×动生电动势定义GGGGGεik=∫LE⋅dl=∫L()vBl×⋅d\nKK例题:已知:v,B,α,L求:εKKKKKv×B解:d()ε=×⋅vBld+++Kdl00=vBsin90dcos(90l−α)+++αK=Bvsinαdlv+++Lε=∫BvsinαdlKL++++B=BvLsinα特例++++++++++++++++K++vK+K++v+KBB++++++++ε=0ε=BvL例题:在均匀磁场B中,金属杆ab沿导体框向右以速度v运动。如图,θ=60o,且dB/dt=0。求其上的ε?i解法一:选逆时针为正方向,由定义GGGGnGaBεiba=×⋅∫b(vBl)ddaθGaolv=∫vBsin30cosπdlbcxb=−1vBl2方向:a⇒bb点电势高\n解法二:用法拉第定律GnGGGBaΦ=B⋅S=B(lx)cosθdθGlv=1Blx()2cxbdΦ1ε=−=−Bld()xidt2dt=−1Blv<0顺时针方向2G例题:金属杆oa长L,在匀强磁场中以角速度Bω逆时针绕o点转动。求杆中感应电动势的大小和方向。G解:杆上取微分元dl,选o指Ga′向a为正方向,根据动生电B动势定义GGGGddεi=×⋅()vBl=−ωlB⋅dloθvla1Gωεωi=−∫lB⋅dl=−ωBL2dlo2a方向:a→oo点电势高\n例题:直导线ab以速率v沿平行于长直载流导线的方向运动,ab与直导线共面,且与它垂直,如图所示。设直导线中的电流强度为I,导线ab长为L,a端到直导线的距离为d,求导线ab中的动生电动势,并判断哪端电势较高。GGGGvbab解:应用εi=∫a(v×B)⋅dlIdLl在导线ab上,在距长直载流导线dll处取一线元dl,方向向右。GGKμIv0d()ε=×⋅=vBlvBldd=dli2πrGbd+LμIvvεε==dd0labab∫∫iad2πrIdLlμ0IvdL+dl=ln2πdεab>0表明电动势的方向由a指向b,b端电势较高。\n例题:有一半圆形金属导线在匀强磁场中作切割磁力KKKK线运动。已知:v,B,R.求:动生电动势。v×BKKKθ解:ddεi=×()vBlibKdlo=vBsin90dcoslθ++d+θ+πθθKεθ==vBR2cosdθvBR2+++++vi∫π−2++R+++方向:a→bb点电势高+a++++结论:半圆形载流导线切割磁力线产生的磁场与其两个端点相连的直导线切割磁力线所产生的磁场相等。任意形状金属导线在匀强磁场中作切割磁力线运动bε=vBlbi+++++++++++l++++K+θlv++++Kv+++++++++++a+++++++a++a′ε=vBlcosθi\n二、感生电动势二、感生电动势感生电场感生电场当导体回路不动,由于磁场变化引起磁通量改变而产生的感应电动势,叫做感生电动势。产生感生电动势的原因是由于变化的磁场在其周围激发了一种电场,这种电场称为感生电场或涡旋电场。涡旋电场的电场是闭合的,它不是保守GKK场,以Ek表示感生电场的场强,即∫Ek⋅dl≠0GG产生感生电动势为εi=∫Ek⋅dlL根据法拉第电磁感应定律dΦdGGε=−m=−B⋅dSi∫ddttSGGGGd∫Ek⋅dl=−∫∫B⋅dSLdtSGGGG∂B或v∫∫LElk⋅=dd−∫∂t⋅S()1S\n考虑同时存在静电场GGv∫El⋅=d0静()2L(1)式+(2)式得GGGGGGGG∂BE⋅+ddddlElEl⋅=⋅=−⋅Svvv∫∫∫∫LLkL总∫静∂tS电磁学的基本方程之一,是静电场的环路定理在非稳恒条件下的推广。感生电场与静电场的比较静电荷静电场场源变化的磁场感生电场KK静电场为保守场(无旋场)∫LE静⋅dl=0环流KKdΦ感生电场为非保守场(有旋场)∫Ek⋅dl=−≠0LdtKKq静电场为有源场v∫ES静⋅d=Sε通量KK0感生电场为无源场v∫ESk⋅=d0S静电场线起于正电荷,止于负电荷场线感生电场线是闭合曲线\n例题:局限于半径R的圆柱形空间内分布有均匀磁场,方向如图。磁场的变化率∂B∂t>0,求:圆柱K内、外的E分布。Gk∂B××××解:选顺时针为正方向S∂trR<×K×××××K×B×××r××KG∂BKE•=ddlS−•vv∫∫LSk∂t×R×L××dB2Er2π=−πrkdtrdB方向:逆时针方向E=−k2dtr>RS′GKL′∂BKG∂BK××××EiiddlS=−vv∫∫LS′′k∂tS⊗∂tK××××Br由图可知,这个圆面积S′包××××rR××括柱体内部分的面积,在圆柱K体外,由于B=0,,∂B∂t=0K而柱体内∂B∂t≠0KK∂∂BBKKdB2∴−=vv∫∫iiddSS−=−πRSS′∂∂ttdt\nKGdB2S′GE•dl=−πRL′∂Bv∫L′kdt××××S⊗∂tdBK××××E2πrR=−π2Brk××××dtr2R××RBdE=−k2drt方向:逆时针方向E2涡RdB−r>R2drtE=krBd−r0方向如图.求:εCD××××G∂BK××o××⊗∂tB××××hC××DL\nKKG解:εik=•v∫Eld∂BLKrBd∂tE=⊗k2dt⊗KoGGGBEddε=•Elθ涡krrBdh=dcoslθθ2dtCDldlhBd=dlrhcosθ=L2dthBd1dBε==dlhLCD∫2dttL2d电动势的方向由C指向D用法拉第电磁感应定理求解××××G1∂B解:CODC所围面积为:S=hLK××o××⊗∂t2BKK1××××磁通量Φm=B⋅S=hLBh2C××DdΦm1dBεi=−=hLLdt2dtKKCDOKKKKKKε=•Edl=•ElElElddd+•+•ikv∫OCDO∫∫∫OCDkkk=++00εCD??\n*练习求杆两端的感应电动势的大小和方向dBε=SK××××∂BoabdodtBR>0××o××⊗∂tS=S+Soabdooabobd××××dbc1312π××=R⋅R+Ra2226RR3d22πBε=+()RR方向a→c412dt§10-4自感和互感一、自感一、自感1、自感现象由于回路中电流产生的磁通量发生变化,而在自己回路中激发感应电动势的现象叫做自感现象,这种感应电动势叫做自感电动势。\n2、自感系数考虑一闭合回路,设其中电流为I。由毕—萨定律知道,线圈在空间激发的磁感应强度与I成正比,因此,穿过回路本身的磁通量也与I成正比,即Φ=LIm当电流随时间变化,磁通量也随时间变化,产生感应电动势dΦdImε=−=−LiddttdΦdImε=−=−Liddtt式中L为比例系数,对于相同的电流变化率,比例系数L越大的线圈所产生的自感电动势越大,自感作用越强,比例系数L叫做自感系数,简称自感。L的大小与回路的几何形状、匝数等因素有关,是一个由回路自身特征决定的电路参数。−1单位:亨利(H)1H1WbA=⋅361H10mH10==μH亨利\n例题:设一的长直螺线管,长为l,截面半径为R,管上绕组的匝数为N,其中通有电流I,求其自感系数。解:∵Bn==μIμ0NIμ0NI20∴Φ=BS=πRll穿过N匝线圈的磁通量为2μπR2N2μ0NI2L=0=μn2VNΦ=πR0mll当线圈中的电流I发生变化时,在N匝线圈中产生的感应电动势为22dNΦμπRNdIm0ε=−=−Lddtlt例题:求一环形螺线管的自感。已知:R、R、h、N12μNI0B=2πrGGμNI0dddΦ=•=BShrm2πrIμNIhR2drR20ddΦΦmm==∫∫R12πR1rμ0NIhR2h=ln()2πR1rdrμNIh2R202ΝΦμNhRNΦ=ln()L==m0ln(2)m2πR1I2πR1\n例题:同轴电缆由半径分别为R和R的两个无限长12同轴导体和柱面组成,电缆中沿内圆筒和外圆筒流过的电流大小相等而方向相反。求:同轴电缆单位长度上的自感。IR解:由安培环路定理可知1IdSμIR2RRB=012rμIdΦ=BdS=lrd2πrR2μIμIlRΦμR2Φ=∫lrd=ln2L==lnR12πr2πR1IlR2π1二、互感二、互感1、互感现象由一个回路中电流变化而在另一个回路中产生感应电动势的现象,叫做互感现象,这种感应电动势叫做互感电动势。\n2、互感系数II21回路2中电流产生的磁场通过回路1磁通量Φ12与I成正比212Φ=MI12122由于I电流变化在回路1出现的感应电动势为2dΦdIε=−12=−M212ddtt12同理Φ=MI21211由于I电流变化在回路2出现的感应电动势为1ddΦIε=−21=−M121ddtt21可以看出,对于相同的电流变化率,比例系数M和12M越大,互感电动势越大,互感作用越强,比例系21数M和M叫做互感系数,简称互感。1221M=M=M实验和理论都可以证明:1221它由两个回路的大小、形状、匝数以及周围磁介质的性质决定.\n例题:有两个直长螺线管,它们绕在同一个圆柱面上。已知:μ、N、N、l、S求:互感系数012N解:BI=μ2202lN2GGNμSΦμ=•==BdSBS2IS012∫21021Nl1lμNNIS01221NΦ=112lΝΦμNNSμNNVM==120121=0122Ill2§10-5磁场的能量当线圈通有电流时,在其周围建立了磁场,所储存的磁能等于建立磁εiR场过程中,电源反抗自感电动势所做i的功。若回路电流以dI/dt>0变化时,电流增加dI,电源克服ε作功为dWidW=–εIdtidI∵εi=−L∴ddWL=IIdtI12储存12WW=∫d=∫0LIId=2LIWLm=I2\n通有电流I的自感线圈中储能:WL=1I2m2以长直螺线管为例L=μnV2我们已知长直螺线管的自感为0设螺线管通有电流I,则其存储的磁能为:WL=1I2=⋅1μnVI22m220而B=μnI0B2即WVm=2μ0∴单位体积储存的磁场能量为WmB21GGwBm===⋅H——磁能密度V22μ0由螺线管特例推出,但以上结论对任意形式的磁场都成立。一般地,对非均匀磁场:GG1Wwmm==⋅∫∫ddVBHVV2\n例题:如图,求同轴传输线之磁能及自感系数R解:由安培环路定律可求H2R1rR,H=02则R1
查看更多