- 2022-08-16 发布 |
- 37.5 KB |
- 58页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
大学物理最后复习
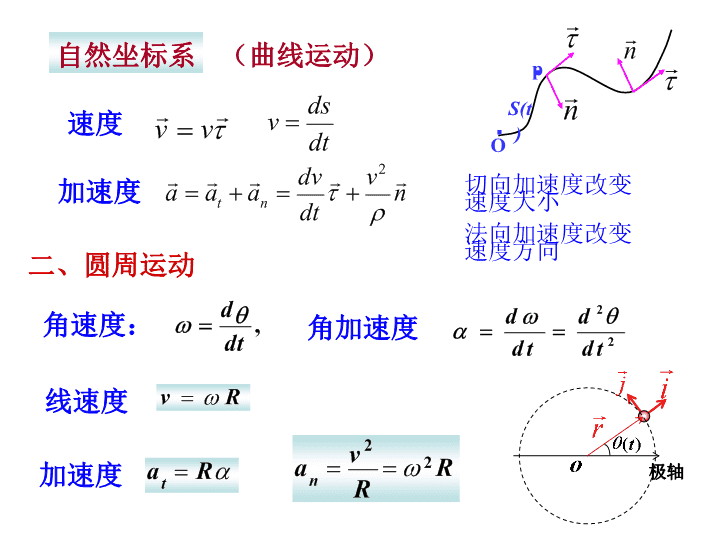
第一章质点运动学运动函数一、描述质点运动的物理量位移速度:切线方向加速度矢量式直角坐标系中:\n自然坐标系速度加速度切向加速度改变速度大小法向加速度改变速度方向线速度加速度二、圆周运动角加速度角速度:极轴··OpS(t)(曲线运动)\n速度变换:加速度变换位矢之间的关系:V物体-静系=V物体-动系+V动系-静系记忆方法:伽利略变换\n第三定律:第一定律:力和惯性第二定律:牛顿三定律解题时注意适应范围采用隔离体法进行受力分析建立坐标系,写分量表达式:Fx=maxFn=manFt=matFy=mayFz=maz第二章:质点和质点系动力学\n动量定理角动量定理动能定理质点系的三个运动定理:★内力能改变系统总动能功能原理:A外+A内非动量守恒定律:常矢量角动量守恒定律:Ek+EP=常量A外=0、A非保内=0,机械能守恒定律:三个守恒定律:\n角动量力矩:相对定点的转动:势能:系统在任意位形的势能等于从此位形变到势能零点时,保守力所做的功\n第三章:刚体定轴转动一、刚体的运动学角量ω、θ、α对刚体上每一质点都相同二刚体动力学定轴转动定律轴向外力矩与角加速度成正比转动惯量:与物体的质量、质量分布和轴的位置有关\n常用的转动惯量的计算公式:(1)圆盘对中心轴:(2)均匀细杆对两种垂直于杆的转轴的转动惯量:轴过端点:轴过中点:\n动能定理机械能守恒对于包含刚体的系统转动动能:轴向外力矩对刚体的功等于刚体转动动能的增量角动量:M=0L=常量——角动量守恒J=常量刚体的角动量定理势能:质心的势能(作业8-6、7)\n物理量随时间按余弦或正弦规律变化第四章简谐振动简谐振动振动速度振动加速度位置函数描述简谐振动的物理量振幅A:物理量变化的最大范围ω=2πv:物体在2π时间内做的全振动次数ωt+φ:决定振动状态的物理量.Φ为初相位\n简谐振动的动力学特征(简谐振动的判据)运动方程F—恢复力k—劲度系数初始条件:\nx参考圆AAt+oxtt=0x=Acos(t+)·矢量长度--振幅角速度--角频率T=0时夹角--初相旋转矢量法可以直观表示三个特征量★旋转矢量法描述简谐振动弹簧振子\n简谐振动的能量动能势能简谐振动系统只受保守力作用,机械能守恒\n阻尼振动振动系统因受阻尼力(-γv)作用,作振幅不断减小的振动.阻尼振动函数:由于阻尼系数β的不同,有三种不同运动状态的解.(2)过阻尼运动β>ω0(3)临界阻尼运动β=ω0(1)小阻尼运动β<ω0阻尼振动周期大于固有周期非周期振动过阻尼临界阻尼欠阻尼xt0\n受迫振动受迫振动稳态解x=Acos(t+)速度极大值速度共振的条件:=0驱动力频率=固有频率位移共振的条件:共振在外来策动力作用下的振动ω为驱动力的频率\n四.简谐振动的合成1.同方向同频率的两简谐振动的合成仍为简谐振动.A,φA1A2Ax合振动加强(1)若两分振动同相21=2k(k=0,1,2,…)\n2.同方向频率相近的两简谐振动合成后,振幅随时间缓慢的周期性变化,称拍.拍的频率为ν拍=∣ν2-ν1∣3.同频率,相互垂直的两简谐振动的合成,一般为椭圆运动质点的轨迹一般是个斜椭圆。当频率不同但成整数比,轨迹闭合——李萨如图。(2)若两分振动反相21=(2k+1)(k=0,1,2,…)A1A2AxФ与振幅大的相同\n第五章波动如果已知平衡位置在x0处,初相为φ0的质点振动方程,波函数的形式:\n动能势能波传播时质元的机械能波的能量能量密度:波传播时,单位体积介质内波的能量平均能量密度:能量密度在一个周期内的平均值适用于各种弹性波\n能流密度:单位时间内通过垂直传播方向的单位面积的能量。平均能流密度:能流密度在一个周期内的平均值。I也称为波的强度单位:瓦/米2,W/m2惠更斯原理波传播时,任一波阵面上的每一点都可以看作发射子波的点波源,以后任意时刻,这些子波的包迹面就是该时刻的波阵面。解释了波的衍射、反射射和折射现象\n波的干涉波的叠加原理:频率相同振动方向相同相位差恒定相干条件发生干涉时空间各点的振动强度形成一个稳定的分布干涉加强干涉减弱两个波源的相位相同时,可用波程差表示:干涉加强干涉减弱\n振幅相同的相干波,在同一直线上沿相反方向传播,叠加后就形成驻波驻波:波形成条件:两列波驻波的表达式:两列波\n固定端反射,界面处为波节自由端反射界面处为波腹L驻波的产生:入射波+反射波驻波的表达式:波腹的位置波节的位置相邻两波节间的质点的振动同相,波节两侧质点的振动反相;驻波振幅驻波相位\n先求平衡位置在x0处:波函数的求法反射波的波函数求法求入射波的波函数求入射波在反射点的振动方程xdyO求反射波的波函数求反射波在反射点的振动方程有半波损失的情况\n七.多普勒效应多普勒效应---因波源或观察者相对波传播的介质运动,致使观察者接收的波的频率发生变化的现象。波源和观察者相对静止时观察者静止,波源运动观察者运动而波源静止(接收的波长发生变化)(接收的波的数目发生变化)\n观察者与波源同时运动记忆方法:约定:VD,Vs是代数量,二者靠近为正、远离为负。(作业13-5、6、7)\n13.5:重点是多普勒效应。汽车接受到得波的频率汽车作为波源发射的波的频率声源处接受到得汽车发射回来的波的频率\n13-6.如图,振动频率为f的声源,以速度u垂直于前方的墙壁运动,在它后方的接收器A,测得从声源发出的声波和墙壁反射回来的声波在接受能点形成的拍,拍频为n,设声速为v,求:写出声源的速度u与f、n、v的函数关系。墙壁接收到的波的频率A点接受到的墙壁反射波的频率即为A点接受到的声源发出的波的频率声源A\n\n7.静止空气中,蝙蝠的速率,飞蛾的逃逸速率,蝙蝠发出55kHz的超声波在空气中的传播速率求:蝙蝠接受到的回波频率。图13-2飞蛾接受:飞蛾作为波源,蝙蝠接受:\n一.狭义相对论的基本假设(基本原理)1.狭义相对性原理:一切彼此作匀速直线运动的惯性系中,物理规律的描述都是等价的2.光速不变原理:在彼此相对作匀速直线运动的任何惯性系中测得的真空中的光速都相等二.洛仑兹变换uP系以速度u相对S系沿X方向作匀速直线运动正变换反变换第六章狭义相对论\n\n1.同时性的相对性三,狭义相对论的时空观沿运动方向上,位置坐标不同的两件事而言,同时性是相对的2.时间间隔的相对性称原时,最短!钟慢效应(时间延缓):3.长度的相对论效应尺缩效应:\n物体沿x方向运动4.相对论速度变换:五.相对论动量P不再与V成正比四.狭义相对论质量v物体的运动速度\n七.相对论能量静止能量八、相对论动能总能量九、相对论能量动量关系质能关系\n所有非惯性系和有引力存在的惯性系对于描述物理现象都是等价的即:物理定律在一切参照系中具有相同的形式等效原理:加速度与引力场等效。广义相性对性原理:十、广义相性论的基本原理光速不变原理依然成立。\n7.高速列车以u速驶过车站,固定在站台上的激光打孔机,两激光束间距为1m。在地面参考系测量:两激光同时射向车厢,打出两个小孔。求(1)在地面参考系测得两孔间距;(2)在列车参考系测得的两孔间距。解:站台K系:在车上打出两个小孔的时空坐标车为系:在车上打出两个小孔的时空坐标在地面(K系)测得两小孔间距在系:\n在系:或:站台K系2先发生或:\n8:地球上测得半人马星座的α星距地球4.3×1016m,一宇宙飞船以v=0.999c的速率通过地球与α星之间的距离。问(1)地球参考系测得此行程的时间;(2)飞船上的时钟记录了多少时间?解:(2)另解:对飞船上的观测者:两件事发生在同一地点飞船通过地球时飞船通过α星时α\n2.如图15-1,在惯性系中x轴上相距L有两只同步钟A和B;在相对S系沿x轴以速度u运动的惯性系中,也有一只同样的钟。若轴平行,当A、相遇时,恰好两钟读数都为零,求:当与B相遇时(1)S系中B钟的读数;(2)系中钟的读数。(2)在系中:(在中,是同一个时钟测出的时间,是原时)LAB(1)在S系中:解:\n3.一个光子在惯性系S中沿y方向以c的速度运动,系以的速度沿x方向运动,求:在系光子运动方向与的夹角。在中只存,分量S:\n4.S、系是坐标轴相互平行的两个惯性系,系相对于S沿x轴正方向匀速运动。一刚性尺静止于S系中,且于x轴成角,而在系中测得该尺与轴成角,试求:S与系的相对运动速度。在S中:设尺长为L在中:\n8.(1)如图16-2所示,一个孤立的作加速运动的电梯,根据爱因斯坦广义相对论理论,在其中观测,光传播的正确路径是[C](根据图中A/B/C三条光线选择);(2)广义相对论的等效原理指出加速度和[引力场]等效;(3)定性完成图16-3经过中子星附近的光线的传播路径光线中子星光源图16-2图16-3\n二、库仑定律方向:由施力电荷指向受力电荷三、静电力的叠加原理第七章:静电学一、电荷的基本性质:两种电荷,量子性,电荷守恒,相对论不变性两个静止点电荷之间的相互作用力带电粒子q(可看成点电荷)在外场中受的力:力偶矩电偶极子在均匀外电场中的受到力矩作用\n四、电场强度某点场强等于单位正电荷在该点所受的电场力五、场强叠加原理某点的电场强度等于所有带电体在该处激发场强的矢量和六、电通量在电场中穿过任意曲面S的电场线条数称通过该面的电通量,用来表示。\n七、高斯定理:内八、场强环路定理:十、电势:九、电势能电势差:电场力所做的功:电荷q在外场中的电势能:电偶极子在外场中的电势能:\n十一、电场的计算:1、应用库伦定律及场强叠加原理计算点电荷系的场强连续带电体的场强2、高斯定理点电荷的场强3、根据场强与电势梯度的关系球对称,轴对称,面对称.\n典型静电场:均匀带电球面均匀带电球体均匀带电无限大平面无限长均匀带电柱体柱面\n无限长直线半无限长直线PEdx\n2、已知场强分布,根据电势的定义,利用积分法求电势十二、计算电势的方法1、已知电荷分布,利用电势叠加原理求电势点电荷系的电势连续带电体的电势点电荷的电势\n十三、静电场中的导体静电平衡条件:E内=0等势体E表等势面表面静电平衡状态:导体各处(内部和表面)均无电荷定向运动。静电平衡时导体上电荷的分布:内部无净电荷,电荷分部在外表面。1.实心导体:2.导体球壳(空腔导体):腔内无带电体外内=0E内=0σ内表=-qE内内q00外腔内有带电体外=Q+q\n3.孤立导体表面上电荷的分布孤立的带电导体,外表面各处的电荷面密度与该处曲率半径成反比。4、导体表面各处的面电荷密度与的该处表面附近场强的关系:由导体内指向外有导体存在时静电场的分析与计算(2)利用电荷守恒(3)利用高斯定律(1)利用静电平衡条件E表面表面静电平衡的导体上的电荷分布Q内=0,σ=ε0E\n十四、静电场中的电介质1.极性分子和非极性分子2.电介质的极化3.电极化强度4.极化电荷与电极化强度的关系:极化电荷的面密度,等于电极化强度沿外法线方向的分量。5.介质中的高斯定理各向同性均匀介质充满电场有介质时的场强\n有电介质时电场、束缚电荷的计算注:要求场分布和各向同性电介质本身具有高度对称性\n孤立导体的电容十五、电容:导体球电容器的电容十六、静电场的能量任意场中存储的能量为电介质中电场的能量密度电容器的能量:均匀电场\n导体中任意一点处的电流密度大小等于载流密度、所带电量及漂移速度的乘积1、电流和电流密度十七、稳恒电流稳恒电场电流强度等于电流密度的通量。电流恒定条件j线不中断。稳恒电流的的电流线一定闭合导体内各处电流密度不随时间变化的电流称为恒定电流或直流电。恒定电流:\n电荷运动伴随能量的转换导体内部恒定电场恒定电场与静电场的区别:2、恒定电场:在恒定电流情况下,不随时间变化的电荷分布所产生的不随时间变化的电场恒定电场高斯定理和场强环路定理在稳恒电场中仍然成立\n4、电源电动势把单位正电荷从电源的负极通过内电路移到正极,非静电力所作的功3、欧姆定律微分形式结论:在垂直电场运动的参考系测E,在平行电场运动的参考系测E不变。十八、运动电荷的电场电荷守恒电场强度的定义和高斯定理仍然成立查看更多