- 2022-08-16 发布 |
- 37.5 KB |
- 21页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
大学物理波动习题
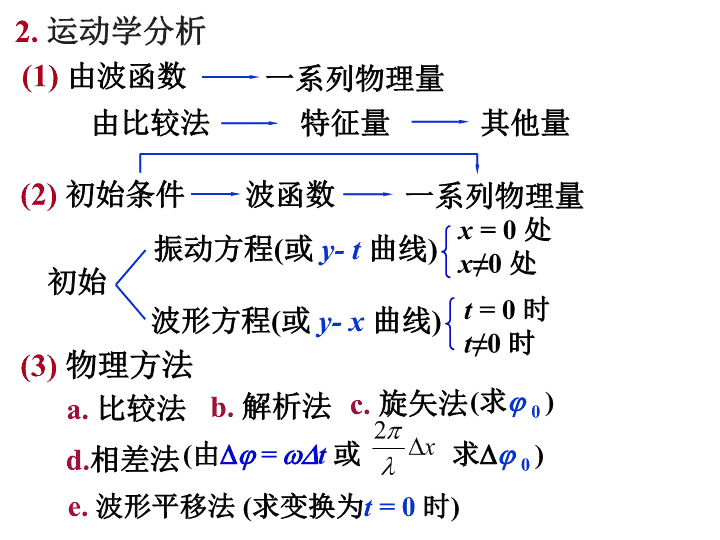
1.掌握机械波产生条件和传播过程的特点2.掌握平面简谐波的波动过程及各物理量3.掌握由已知质点的振动方程得出平面谐波方程的基本方法4.理解波的干涉现象及相干条件一、基本要求\n一.(一维)简谐波的运动学分析1.波函数—描述波线上各质元的集体振动规律x处质元振动方程波形方程x一定t一定关键:特征量(A、、u、……)与坐标系(原点,正向)选择有关问题0—x=0处t=0时质元状态二、基本内容\n2.运动学分析一系列物理量(1)由波函数由比较法特征量其他量(3)物理方法a.比较法e.波形平移法(求变换为t=0时)一系列物理量(2)初始条件波函数振动方程(或y-t曲线)初始波形方程(或y-x曲线)x=0处x≠0处t=0时t≠0时(求0)c.旋矢法b.解析法d.相差法(由=t或求0)\n3.相差法(同一列波)区分超前或滞后同一质元不同时刻同一时刻不同质元二.波的能量——传播特性1.质元能量(不守恒)(同相位)周期性函数(一个周期)2.平均能量密度=常数3.能流(功率)4.能流密度(强度)\n三.波的干涉1.相干波如—叠加中的一个特例条件同(振动)方向同频率相差恒定2.两相干波相位差—空间位置函数初相差不同路径相位跃变影响3.强弱空间分布规律—取决于(同相点)—相长(反相点)—相消相长相消含相位跃变影响(0,/2)\n4.一维驻波(干涉的特例)(1)驻波方程分段反相振动,波形不移动,I左+I右=0不传播能量波腹与波节(2)波腹与波节求解干涉法(由求解),由反射端(节或腹)倒推由驻波方程求解,\n5.相位跃变问题—推广到光学反射端恒为波节(固定端)相当(/2)有相位跃变反射端恒为波腹无相位跃变(自由端)波疏介质波密介质透射波不存在相位跃变问题四.Doppler效应—连线方向一般:接近远离\n1、已知波动方程讨论下列问题(1)式中 是否就是波源的初相?不一定!是坐标原点处振动的初相,( 时, 处的初相),不一定是波源.(2)式中“+”“-”如何确定?由波的传播方向和ox轴的正方向来确定。当传播方向沿着ox轴正方向时,取“-”号当传播方向沿着ox轴负方向时,取“+”号三、选择题与讨论题\n(4)任一时刻波线上 处的相位为多少?(5)任一时刻,波线上位于 和 两点的相位差为多少?与波源有关: (均匀介质无吸收)(3)式中哪些量与波源有关;哪些量与介质有关?与介质有关:\n2、横波的波形图示。讨论(1)若设波沿ox轴负向传播,图上A,B,C,D点运动方向如何?(2)若图示为 的波形图,则坐标原点处质点的初相为多少?时,o点的位移为零,且 ,则\n(3)若图示为 的波形图则坐标原点处质点的初相位为多少?将波形移动(向 相反方向)半波长,知时,o点的位移为零,且 ,则\n3、平面简谐波在弹性媒质中传播,在媒质质元从最大位移处回到平衡位置的过程中:(A)它的势能转换成动能;(B)它的动能转换成势能;(C)它从相邻的一段媒质质元获得能量,其能量逐渐增加;(D)它把自己的能量传给相邻的一段媒质质元,其能量逐渐减少。[C]\n4、两列相干波,其波动方程为y1=Acos2(tx/)和y2=Acos2(t+x/),沿相反方向传播叠加形成的驻波中,各处的振幅是:[D]\n6、如图一平面简谐波沿ox轴正方向传播,波长为λ,若P1点处的质点振动方程为则P2点的振动方程为_______________________________与P1振动状态相同的那些点的位置是____________________________________。\n5、设声波在媒质中的传播速度为u,声源的频率为νS,若声源S不动,而接收器R相对于媒质以速度vR沿S、R连线向着声源S运动,则接收器R接收到的信号频率为[B]\n6.一频率为1kHz的声源以vs=34m/s的速率向右运动。在声源的右方有一反射面,该反射面以v1=68m/s的速率向左运动。设空气中的声速u=340m/s。则反射波在空气中的波长为。反射波在空气中的频率为:反射波在空气中的波长为:0.2m\n1、波动方程 ,求波的振幅,波长,频率,周期和波速。解:用比较法求解平面谐波的标准方程故将已知方程化为所以四、计算题\n也可按各量的物理意义来求解如波长是指同一时刻,同一波线上相位差为 的相邻两质点间的距离又如波速是相位传播的速度,设时刻点的相位在 时刻传播到 点,则有\n解1直接法Q与P点的距离设为r:则2.有一平面简谐波在介质中传播,波速u=100m/s,波线上右侧距波源o(坐标原点)为75.0m处的一点P的运动方程为求:波向x轴正方向传播时的波动方程。(m)oPQxx75.0mu\noPQxx75.0mu解2设波动方程的一般式将u=100m/s代入,且x=75.0m则得P点的振动方程与题目中P点的振动方程比较,得到则所求的波动方程为与解1结果相同\n(1)波动方程4、一平面简谐波向ox轴负向传播,已知其 时的波形曲线,设角频率为ω,波速为 ,振幅为A,波长为,求(2)距o点为 处质点的振动方程(3)距o点为 处质点在 时的振动速度解:(1)(2)(3)查看更多