- 2022-08-16 发布 |
- 37.5 KB |
- 42页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
大学物理复习2
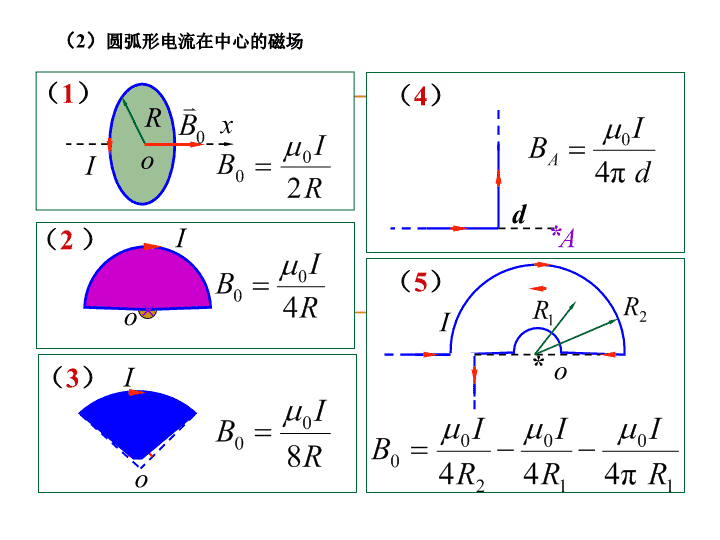
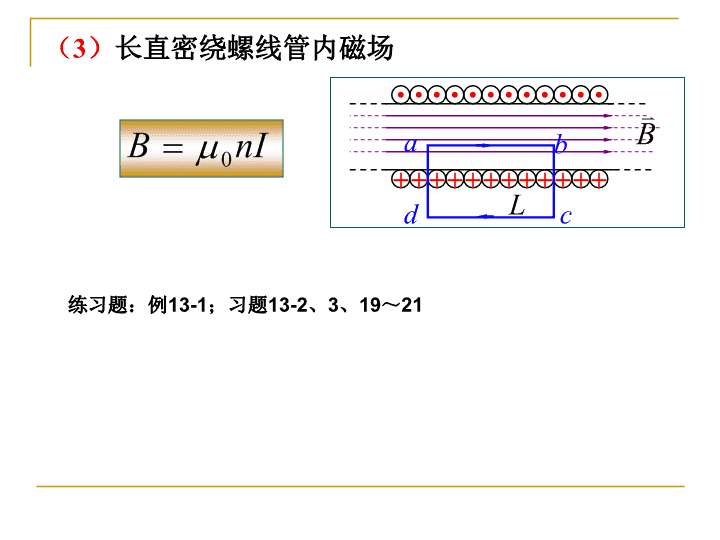
13章稳恒电流的磁场1、叠加原理求磁感强度:要求记住:有限长、无限长、圆弧形电流在中心、长直螺线管的磁感应强度公式。(1)一段直线电流的磁场I①导线无限长,②导线半无限长,③P点在导线延长线上,\noI(5)*Ad(4)*o(2R)I+R(3)oIIRo(1)x(2)圆弧形电流在中心的磁场\n(3)长直密绕螺线管内磁场++++++++++++abdc练习题:例13-1;习题13-2、3、19~21\n例13—1将一无限长导线的中部折成一个长为a宽为b的开口矩形,如15—16所示,并使此导线通以电流I,求矩形中心O处的磁感应强度B。解:O点的磁感应强度B可看作一无限长直载流直导线与一矩形载流导线在O点产生的磁感应强度的矢量叠加Bo=B矩+B直B直的大小为B直的方向垂直纸面向外.B矩可以看成四段载流导线在O点产生的磁感应强度的叠加,B矩的大小为:B矩=2Ba+2BbB矩的方向垂直纸面向里.\nBa与Bb分别为长为a的载流直导线与长为b的载流直导线在O点处产生的磁感强度,可由载流直导线外任一点磁感强度的公式:计算,则其中得故B矩=2Ba+2Bb=\n由于B直与B矩方向相反,所以,Bo=B矩-B=O点处磁感应强度BO的方向垂直纸面向里。此例题也可将整个载流导线分为五段载流直导线在O点处磁感应强度的矢量叠加。其中有两段为半无限长载流直导线,两段长为a的载流直导线,一段长为b的载流直导线,分别求出它们在O点处的磁感应强度,然后矢量叠加。练习题:习题13-2;13-3P104\n13-2一无限长直导线在P处弯成半径为R的圆。当通以电流I时,圆心O处的磁感应强度的大小为()(A)(B)(C)(D)13-3边长为a的正方形线圈中通有电流I,此线圈在P点(见图)产生的磁感应强度的大小为()(A)0(B)(C)(D)(D)(B)\n练习题;习题13-19如题图所示,AB、CD为长直导线,BC为圆心在O点、半径为R的一段圆弧形导线,若导线通以电流I,求圆心O点处的磁感应强度。RoIBACD解:BAB=0方向向里方向向里方向向里\nRoIbacdIRRexyz练习题;习题13-20真空中,一无限长直导线abcde弯成图示的形状,并通有电流I。bc直线在xOy平面内,cd是半径为R的1/4圆弧,ab,de分别在x轴和z轴上;Ob=Oc=Od=R。求O点处的磁感应强度。方向沿x轴正向解:Bab=Bde=0方向沿z轴正向\n求:三角形框在其中心O点产生的B0练习题;习题13-21真空中有一边长为l、电阻均匀的正三角形导线框架。另有两条与三角形底边平行的长直导线1和2分别接在三角形的a、b两点,如图所示。设导线中的电流为I,求正三角形中心O点的磁感应强度。c12方向向外方向向里方向\n2、磁通量的简单求解:练习题:例13-4;\n例13-4无限长导线通电流I,旁边有一个与它共面的单匝矩形线圈,各部分尺寸如图所示,计算通过矩形线圈的磁通量.解:在r处取面元ds通过ds的磁通式中\n3、理解磁场中的安培环路定理:练习题:思考题13-7思13-7图中两导线的电流I1和I2均为4A;试对如图所示的三个闭合回路a、b、c,分别写出安培环路定理等式右边电流的代数和,并讨论:1在每个闭合回路上各点的B是否相等?2在闭合回路c上各点的B是否为零?\n13-7思13-7图中两导线的电流I1和I2均为4A;试对如图所示的三个闭合回路a、b、c,分别写出安培环路定理等式右边电流的代数和,并讨论:1在每个闭合回路上各点的B是否相等?2在闭合回路c上各点的B是否为零?\n4、带点粒子在匀强磁场的运动问题:(1)运动方向与磁场方向平行+=0F=0粒子作匀速直线运动(2)运动方向与磁场方向垂直FBR+v作匀速圆周运动轨道半径\n练习题:式13-34;习题13-7一个动量为p的电子,沿图示方向入射并能穿过一宽度为D,磁感应强度为B的均匀磁场区域。则该电子出射方向与入射方向间的夹角为(C)(A)(B)(C)(D)Rα(C)\n5、载流导线在匀强磁场中受磁力的计算:大小:例13—8一段长为l,载流为I2的直导线AC,置于无限长载流直导线I1附近,位置和尺寸如图13—37所示,求直导线AC所受的安培力。B的方向垂直纸面向里.在AC上离I1为x处了电流元I2dx,则其受到磁场的安培力为取AC上不同位置的电流元时,则其受力方向相同,均垂直AC向上。于是整段导线AC受到的力的大小为或用矢量式表示为\n14章电磁感应电磁场1、法拉第电磁感应定律的运用:练习题:例14-1、2\n解:取顺时针方向为回路正方向例14-1、一长直导线通以电流,旁边有一个共面的矩形线圈abcd。求:线圈中的感应电动势。odcbarxixdx当时,,则,的方向为逆时针方向\n解:例14-2、一种测铁质中磁感应强度的实验装置如图所示。被测试样做成截面积为S的圆环,环上绕有两个绕组。匝数为N1的线圈与电源相连,匝数为N2、电阻为R的线圈两端接一冲击电流计。设铁环原来没被磁化。当合上电键使N1中电流从零增大到I时,冲击电流计测得通过它的电量为q。求与电流I对应的铁环中的磁感应强度B的大小。合上电键S使N1中的电流从零增大到I时,线圈N2产生的感应电动势大小为N2回路中的感应电流为\n由此得铁环中的B设N1中电流从零增大到I需要的时间为t,则在该时间内通过N2回路的感应电荷为\n2、动生电动势公式(14-10)的运用:练习题:例14-3、4;习题14-16、17\n解1:电动势的方向Ao,即o端电势高例14-3、长度为L的导体棒在均匀磁场B中以角速度绕o端逆时针匀速转动,求棒上的感应电动势。根据动生电动势定义求在l处取线元dl,它产生的动生电动势为整条棒的动生电动势大小\n例14-4在匀强磁场中,置有面积为S的可绕轴转动的N匝线圈.若线圈以角速度作匀速转动.求线圈中的感应电动势.\n已知求解设时,与同向,则令则\n习题14-16、1714-16一导线被弯成如题14-16图所示的形状,abc为半径为R的四分之三圆弧,直线段Oc的长度为R。若此导线放在均匀磁场B中,B的方向垂直纸面向里。导线以角速度在图面内绕O点匀速转动,则此导线中的动生电动势大小,电势最高的点是。a点\n14-17长度为L的导体棒ab在均匀磁场中,绕过c点并与棒垂直的轴以角速度匀速转动,,则,,。电动势的方向ca,即a端电势高,所以\n3、简单的感生电场问题求解:练习题:例14-5;习题14-5\n设一个半径为R的长直载流螺线管,内部磁场强度为,若为大于零的恒量。求管内外的感应电场。例14-5轴对称分布的变化磁场产生的感应电场\n14-5如图所示,均匀磁场B被限制在半径为R的无限长圆柱形空间内。若磁场的变化率为正的常数,则圆柱形空间外距轴线为r(r>R)处的P点的感生电场的大小为()(A)0(B)(C)(D)(C)\n4、自感系数和互感系数的定义及求解:思考题14-9;例14-8,14-10;习题14-9,14-18—自感系数一个线圈的自感系数L,由线圈的形状、大小、匝数、周围介质分布等因素决定。与I无关.单位:H(亨利)\n例14-8、长为l的螺线管,横断面为S,线圈总匝数为N,管中磁介质的磁导率为,求自感系数。解:为线圈体积设螺线管通电流I管内磁场通过线圈的全磁通螺线管的自感系数\n提高L的途径增大V提高n放入值高的介质求L的步骤:①设线圈中通有电流I②求B③求全磁通④\n12I1I2(2)互感系数如图,设回路1中通电流I1,产生穿过回路2的全磁通同理,回路2中通电流I2,产生穿过回路1的全磁通比例系数称为两线圈的互感系数。它仅与两回路的形状,相对位置,周围磁介质有关。与I1、I2无关。M的单位与L相同。\n例14-10、设在一长l=1m,横断面积S=10cm2,密绕N1=1000匝线圈的长直螺线管中部,再绕N2=20匝的线圈。(1)计算互感系数;(2)若回路1中电流的变化率为10A/s,求回路2中引起的互感电动势;(3)M和L1、L2的关系。解:(1)设原线圈通电流I1管内磁场通过副线圈的全磁通互感系数\n(2)回路2中的互感电动势(3)M与L的关系已知两线圈的互感系数因为两线圈的自感系数\n一般情况下:k称为“耦合系数”,由两线圈的相对位置确定\n14-9无限长直导线与一矩形线圈共面,如图所示。直导线穿过矩形线圈(但彼此绝缘),则直导线与矩形线圈的互感系数为()(A)0(B)(C)(D)(C)\n14-18在一纸筒上绕有两个相同的线圈ab和a’b‘,如题14-18图所示,两个线圈的自感都是0.05H。若把a和a’相接,则b和b‘间的自感;若把a’与b相接,则a和b‘间的自感H;若a和a’相接,b和b‘也相接,则a和b间的自感H。(1)相当于反串(2)相当于n增大一倍(3)相当于n不变,导线增粗\n5、了解位移电流的定义,麦氏方程组积分形式及其物理意义:练习题14-12,14-13,14-19定义:位移电流位移电流密度14-12在感应电场中,电磁感应定律可写成,式中Ei为感应电场的电场强度。此式表明()(A)闭合曲线l上Ei处处相等(B)感应电场是保守力场(C)感应电场的力线不是闭合曲线(D)在感应电场中不能像对静电场那样引入电势的概念(D)\n14-13如图所示。两圆片构成的平行板电容器(忽略边缘效应)充电时,沿环路L1和L2磁场强度H的环流中,必有()(C)\n6、了解磁场能量密度公式:练习题:习题14-19电磁场能量能量密度静电场的能量密度:稳恒磁场的能量密度:变化的电磁场同时具有电场能和磁场能:14-19两个长度相同,匝数相同,截面积不同的长直螺线管,通以相同大小的电流,现在将小螺线管完全放入大螺线管里(两者轴线重合),且使两者产生的磁场方向一致,则小螺线管内的磁能密度是原来的倍;若使两螺线管产生的磁场方向相反,则小螺线管内的磁能密度为。40(1)B=2B0(2)B=0查看更多