- 2022-08-16 发布 |
- 37.5 KB |
- 9页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
大学物理习题11
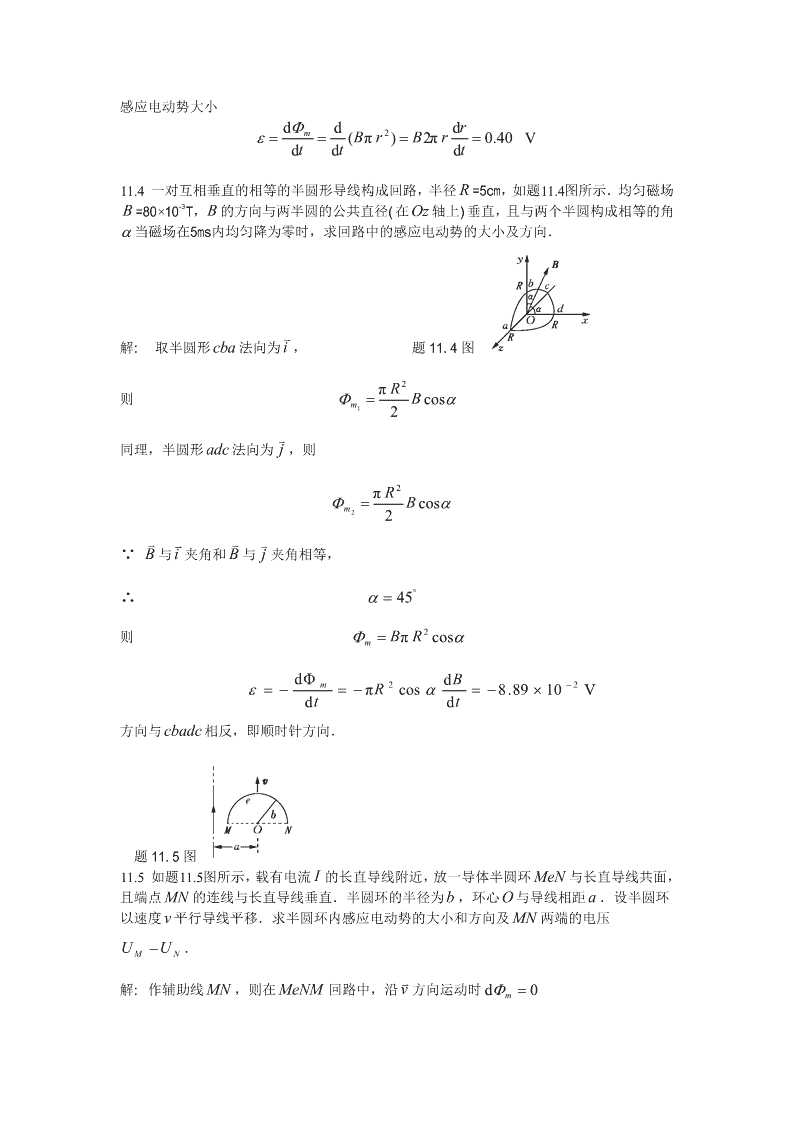
习题1111.1选择题(1)一圆形线圈在磁场中作下列运动时,那些情况会产生感应电流()(A)沿垂直磁场方向平移;(B)以直径为轴转动,轴跟磁场垂直;(C)沿平行磁场方向平移;(D)以直径为轴转动,轴跟磁场平行。[答案:B](2)下列哪些矢量场为保守力场()(A)静电场;(B)稳恒磁场;(C)感生电场;(D)变化的磁场。[答案:A](3)用线圈的自感系数L来表示载流线圈磁场能量的公式12()W=LIm2(A)只适用于无限长密绕线管;(B)只适用于一个匝数很多,且密绕的螺线环;(C)只适用于单匝圆线圈;(D)适用于自感系数L一定的任意线圈。[答案:D](4)对于涡旋电场,下列说法不正确的是():(A)涡旋电场对电荷有作用力;(B)涡旋电场由变化的磁场产生;(C)涡旋场由电荷激发;(D)涡旋电场的电力线闭合的。[答案:C]11.2填空题(1)将金属圆环从磁极间沿与磁感应强度垂直的方向抽出时,圆环将受到。[答案:磁力](2)产生动生电动势的非静电场力是,产生感生电动势的非静电场力是,激发感生电场的场源是。[答案:洛伦兹力,涡旋电场力,变化的磁场](3)长为l的金属直导线在垂直于均匀的平面内以角速度ω转动,如果转轴的位置在,这个导线上的电动势最大,数值为;如果转轴的位置在,整个导线上的电动势最小,数值为。12[答案:端点,Bωl;中点,0]2v11.3一半径r=10cm 的圆形回路放在B=0.8T的均匀磁场中.回路平面与B垂直.当回路半dr-1径以恒定速率=80cm·s收缩时,求回路中感应电动势的大小.dt2解:回路磁通Φ=BS=Bπrm\n感应电动势大小dΦmd2drε==(Bπr)=B2πr=0.40Vdtdtdt11.4一对互相垂直的相等的半圆形导线构成回路,半径R=5cm,如题11.4图所示.均匀磁场B-3=80×10T,B的方向与两半圆的公共直径(在Oz轴上)垂直,且与两个半圆构成相等的角α当磁场在5ms内均匀降为零时,求回路中的感应电动势的大小及方向.v解:取半圆形cba法向为i,题11.4图2πR则Φ=Bcosαm12v同理,半圆形adc法向为j,则2πRΦ=Bcosαm22vvvv∵B与i夹角和B与j夹角相等,°∴α=452则Φ=BπRcosαmdΦm2dB−2ε=−=−πRcosα=−8.89×10Vdtdt方向与cbadc相反,即顺时针方向.题11.5图11.5如题11.5图所示,载有电流I的长直导线附近,放一导体半圆环MeN与长直导线共面,且端点MN的连线与长直导线垂直.半圆环的半径为b,环心O与导线相距a.设半圆环以速度v平行导线平移.求半圆环内感应电动势的大小和方向及MN两端的电压U−U. MNv解:作辅助线MN,则在MeNM回路中,沿v方向运动时dΦ=0m\n∴ε=0MeNM即ε=εMeNMNa+bµIva−b0又∵ε=vBcosπdl=ln<0MN∫a−b2πa+b所以ε沿NeM方向,MeNµIva+b0大小为ln2πa−bM点电势高于N点电势,即µ0Iva+bU−U=lnMN2πa−b题11.6图11.6如题11.6所示,在两平行载流的无限长直导线的平面内有一矩形线圈.两导线中的电流dI方向相反、大小相等,且电流以的变化率增大,求:dt(1)任一时刻线圈内所通过的磁通量; (2)线圈中的感应电动势. 解:以向外磁通为正则b++aµIdaµIµIlb+ad+a000(1)Φ=ldr−ldr=[ln−ln]m∫∫b2πrd2πr2πbddΦµld+ab+adI0(2)ε=−=[ln−ln]dt2πdbdt11.7如题11.7图所示,用一根硬导线弯成半径为r的一个半圆.令这半圆形导线在磁场中以频率f绕图中半圆的直径旋转.整个电路的电阻为R.求:感应电流的最大值.题11.7图vvπr2解:Φ=B⋅S=Bcos(ωt+ϕ)m02\n2dΦmBπrωε=−=sin(ωt+ϕ)i0dt2∴22BπrωBπr22ε==2πf=πrBfm2222εmπrBf∴I==RR11.8如题11.8图所示,长直导线通以电流I=5A,在其右方放一长方形线圈,两者共面.线-1圈长b=0.06m,宽a=0.04m,线圈以速度v=0.03m·s 垂直于直线平移远离.求:d=0.05m时线圈中感应电动势的大小和方向.题11.8图v解:AB、CD运动速度v方向与磁力线平行,不产生感应电动势.DA产生电动势AvvvµI0ε=(v×B)⋅dl=vBb=vb1∫D2πdBC产生电动势CvvvµI0ε=(v×B)⋅dl=−vb2∫B2π(a+d)∴回路中总感应电动势µ0Ibv11−8ε=ε+ε=(−)=1.6×10V122πdd+a方向沿顺时针.v11.9长度为l的金属杆ab以速率v在导电轨道abcd上平行移动.已知导轨处于均匀磁场Bvv中,B的方向与回路的法线成60°角(如题11.9图所示),B的大小为B=kt(k为正常).设t=0时杆位于cd处,求:任一时刻t导线回路中感应电动势的大小和方向.vv1122解:Φ=B⋅dS=Blvtcos60°=ktlv=klvtm∫22dΦm∴ε=−=−klvtdt即沿abcd方向顺时针方向.\n题11.9图v11.10一矩形导线框以恒定的加速度向右穿过一均匀磁场区,B的方向如题11.10图所示.取逆时针方向为电流正方向,画出线框中电流与时间的关系(设导线框刚进入磁场区时t=0).dΦ解:如图逆时针为矩形导线框正向,则进入时<0,ε>0;dt题11.10图(a)题11.10图(b)dΦ在磁场中时=0,ε=0;dtdΦ出场时>0,ε<0,故I−t曲线如题10-9图(b)所示.dt题11.11图l11.11导线ab长为l,绕过O点的垂直轴以匀角速ω转动,aO=磁感应强度B平行于转3轴,如图11.11所示.试求:(1)ab两端的电势差;(2)a,b两端哪一点电势高?解:(1)在Ob上取r→r+dr一小段2l2Bω2则ε=3ωrBdr=lOb∫09l12同理ε=3ωrBdr=BωlOa∫01812212∴ε=ε+ε=(−+)Bωl=BωlabaOOb1896(2)∵ε>0即U−U<0abab∴b点电势高.\n题11.12图11.12如题11.12图所示,长度为2b的金属杆位于两无限长直导线所在平面的正中间,并以v速度v平行于两直导线运动.两直导线通以大小相等、方向相反的电流I,两导线相距2a.试求:金属杆两端的电势差及其方向.解:在金属杆上取dr距左边直导线为r,则Bvvva+bµ0Iv11−µ0Iva+bε=(v×B)⋅dl=−(+)dr=lnAB∫A∫a−b2πr2a−rπa−b∵ε<0AB∴实际上感应电动势方向从B→A,即从图中从右向左,µIva+b0∴U=lnABπa−b题11.13图v11.13磁感应强度为B的均匀磁场充满一半径为R的圆柱形空间,一金属杆放在题11.13图中位dB置,杆长为2R,其中一半位于磁场内、另一半在磁场外.当>0时,求:杆两端的感应电dt动势的大小和方向.解:∵ε=ε+εacabbcdΦ1d323RdBε=−=−[−RB]=abdtdt44dt22dΦdπRπRdB2ε=−=−[−B]=abdtdt1212dt223RπRdB∴ε=[+]ac412dtdB∵>0dt∴ε>0即ε从a→cac\ndB11.14半径为R的直螺线管中,有>0的磁场,一任意闭合导线abca,一部分在螺线管dt内绷直成ab弦,a,b两点与螺线管绝缘,如题10-13图所示.设ab=R,试求:闭合导线中的感应电动势.解:如图,闭合导线abca内磁通量vvπR23R2Φ=B⋅S=B(−)m642πR32dB∴ε=−(−R)i64dtdB∵>0dt∴ε<0,即感应电动势沿acba,逆时针方向.i题11.14图题11.15图11.15如题11.15图所示,在垂直于直螺线管管轴的平面上放置导体ab于直径位置,另一导体cd在一弦上,导体均与螺线管绝缘.当螺线管接通电源的一瞬间管内磁场如题11.15图示方向.试求: (1)ab两端的电势差; (2)cd两点电势高低的情况. vvvdBvv解:由E⋅dl=−⋅dS知,此时E以O为中心沿逆时针方向.∫∫l旋dt旋v(1)∵ab是直径,在ab上处处E与ab垂直旋v∴⋅dl=0∫l旋∴ε=0,有U=Uababcvv(2)同理,ε=E⋅dl>0dc∫d旋∴U−U<0即U>Udccd\n题11.16图11.16一无限长的直导线和一正方形的线圈如题11.16图所示放置(导线与线圈接触处绝缘).求:线圈与导线间的互感系数.解:设长直电流为I,其磁场通过正方形线圈的互感磁通为2aµIaµIaΦ=30dr=0ln212∫a2πr2π3Φµa120∴M==ln2I2π11.17两线圈顺串联后总自感为1.0H,在它们的形状和位置都不变的情况下,反串联后总自感为0.4H.试求:它们之间的互感.解:∵顺串时L=L+L+2M12反串联时L′=L+L−2M12∴L−L′=4ML−L′M==0.15H4题11.18图11.18一矩形截面的螺绕环如题11.18图所示,共有N匝.试求: (1)此螺线环的自感系数; (2)若导线内通有电流I,环内磁能为多少?解:如题11.18图示(1)通过横截面的磁通为bµNIµNIhb00Φ=∫hdr=lna2rπ2πa2µ0NIhb磁链Ψ=NΦ=ln2πa\n2Ψµ0Nhb∴L==lnI2πa12(2)∵W=LIm222µ0NIhb∴W=lnm4πa11.19一无限长圆柱形直导线,其截面各处的电流密度相等,总电流为I.求:导线内部单位长度上所储存的磁能.µI0r解:在r查看更多
相关文章
- 当前文档收益归属上传用户