大学物理2.212665

大学物理2.212665

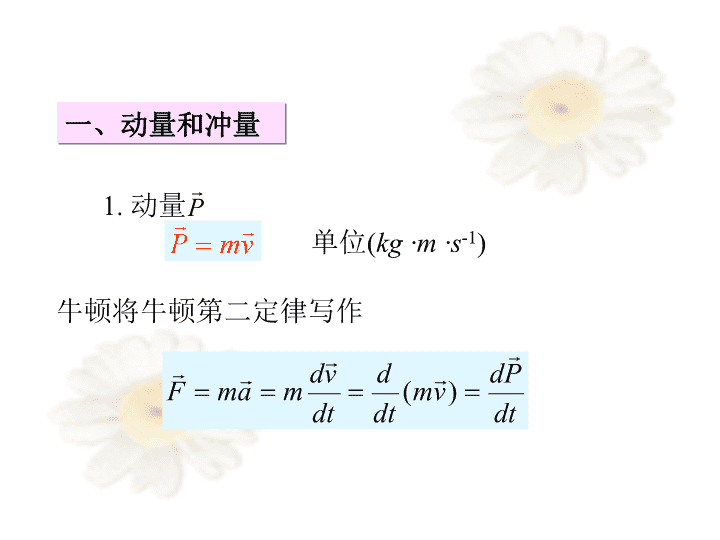
力学现象和力学过程总是在一定的时空中发生和发展的，因此必然涉及到力对时间和空间的积累问题。2.2动量与动量守恒\n一、动量和冲量1.动量单位(kg·m·s-1)牛顿将牛顿第二定律写作\n2.冲量恒力的冲量变力的冲量\n在时间t1t2间隔内，力F是变化的，求t1t2时间间隔内的总冲量将区间t1t2分成无穷多小段；取其中一小段dt,这一小段内力的冲量t1t2的总冲量为上式的积分t1F0tt2dtF\n二、质点动量定理质点动量定理在一段时间间隔内，质点所受合外力的冲量等于这段时间内质点动量的增量。\n分量式平均冲力\nm2m1m3m4三、质点系动量定理由若干个质点所组成的系统叫质点系，也称作一个力学系统。F1f1F2f2F3f3F4f4外力内力\n对每一个质点利用动量定理质点i对所有质点求和由n个质点组成的力学系统合外力的冲量等于系统总动量的增量。•••••\n四、动量守恒定律若系统所受的合外力＝0系统总动量守恒\n分量式若系统在某方向上所受的合外力为零，则系统在该方向上的动量守恒。\n五应用TmgOxyZ例1一圆锥摆，角速度为（恒定）,摆球质量为m，摆线长为，如图所示。试计算四分之一周期内绳子张力的冲量。\n\n例2一质量为m的物体,原来向北运动,速率为vo,它突然受到外力的打击,变为向东运动,速率为。求打击过程外力的冲量大小和方向。oXY解:根据动量定理忽略重力的冲量,则外力的冲量为与水平方向的夹角\n例3：一质量为m=1kg的质点从静止出发沿X轴作直线运动，受到的合外力为F=1+t（N），求t=3s时，质点的速度。解：F(N)O1t(s)32?\n例4：在一光滑的桌面上，一弹性小球和另一静止的完全弹性小球发生碰撞。试证：碰撞之后，两球的运动方向互相垂直。证明：\n例5：一辆煤车以v=3m/s的速率从煤斗下面通过,每秒钟落入车厢的煤为△m=500kg。如果车厢的速率保持不变,应用多大的牵引力拉车厢?（2）设以地面为参考系，建立直角坐标系如图，解:(1)研究对象：t时刻车中煤与车的总质量mt+dt时刻车与煤的质量m+dmmdmOXt时刻和t+dt时刻系统水平总动量分别为:dt时间内系统水平总动量增量为:由动量定理可得:\n例6火箭飞行原理自由飞行。选地面参考系，并建立直角坐标系vMdmuM-dmv+dvOt+dttt时刻，系统动量：动量守恒：t+dt时刻，系统动量：单级最大7千米/秒。\n六质心XZYOm2r2m1r1crcmirirNmN对于分立体系：直角坐标系下：1概念：\n对于连续体：直角坐标系下：XZYOcrcdmr\n2：质心运动定理——质心运动定理\n例7一质量m1=50kg的人站在一条质量m2=200kg,长度l=4m的船头上。开始时船静止,求当人从船头走到船尾时船移动的距离d=？xCbC’b0yx1x’1x2x’2dd\n当人在船左端时,人和船这个系统的质心坐标为当人在船右端时,人和船这个系统的质心坐标为解:取人和船为系统,该系统在水平方向不受外力,因而水平方向的质心速度不变,即质心始终静止不动。由于所以即:求当人从船头走到船尾时船移动的距离