大学物理剩余

大学物理剩余

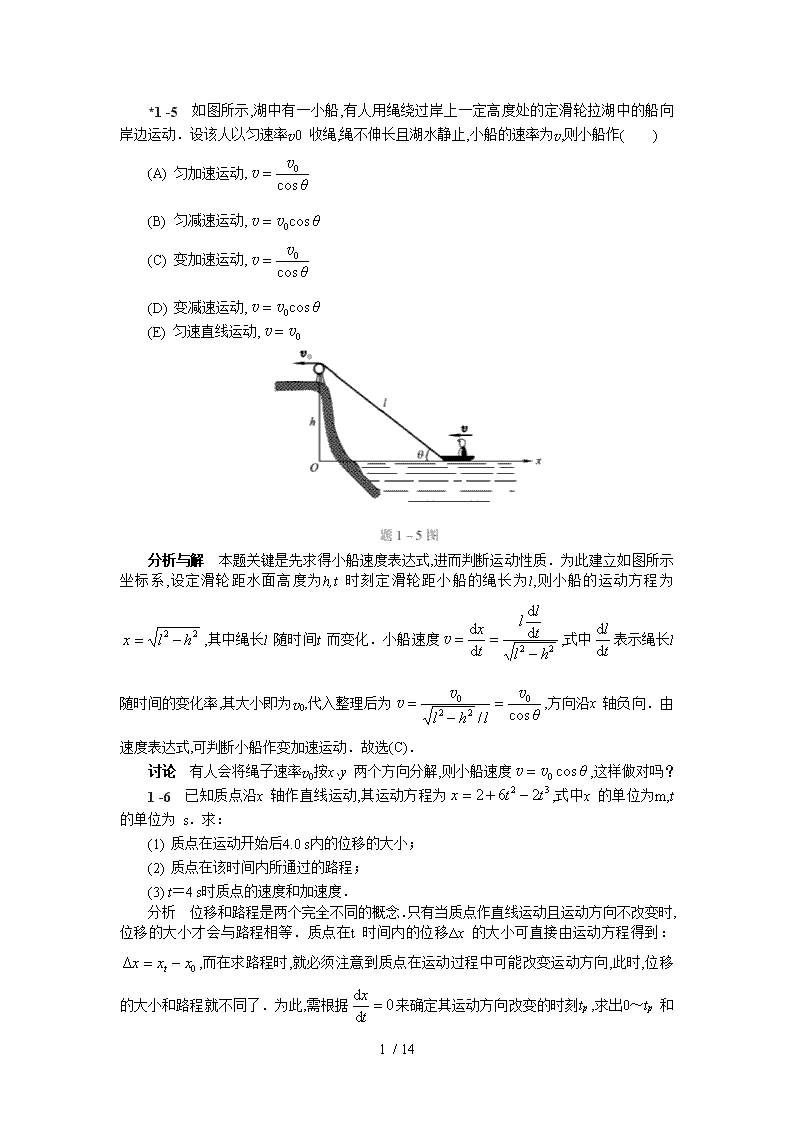
*1-5　如图所示,湖中有一小船,有人用绳绕过岸上一定高度处的定滑轮拉湖中的船向岸边运动．设该人以匀速率v0收绳,绳不伸长且湖水静止,小船的速率为v,则小船作(　　)(A)匀加速运动,(B)匀减速运动,(C)变加速运动,(D)变减速运动,(E)匀速直线运动,分析与解　本题关键是先求得小船速度表达式,进而判断运动性质．为此建立如图所示坐标系,设定滑轮距水面高度为h,t时刻定滑轮距小船的绳长为l,则小船的运动方程为,其中绳长l随时间t而变化．小船速度,式中表示绳长l随时间的变化率,其大小即为v0,代入整理后为,方向沿x轴负向．由速度表达式,可判断小船作变加速运动．故选(C)．讨论　有人会将绳子速率v0按x、y两个方向分解,则小船速度,这样做对吗？1-6　已知质点沿x轴作直线运动,其运动方程为,式中x的单位为m,t的单位为s．求：(1)质点在运动开始后4.0s内的位移的大小；(2)质点在该时间内所通过的路程；(3)t＝4s时质点的速度和加速度．分析　位移和路程是两个完全不同的概念．只有当质点作直线运动且运动方向不改变时,位移的大小才会与路程相等．质点在t时间内的位移Δx的大小可直接由运动方程得到：,而在求路程时,就必须注意到质点在运动过程中可能改变运动方向,此时,位移的大小和路程就不同了．为此,需根据来确定其运动方向改变的时刻tp,求出0～tp和14/14\ntp～t内的位移大小Δx1、Δx2,则t时间内的路程,如图所示,至于t＝4.0s时质点速度和加速度可用和两式计算．解　(1)质点在4.0s内位移的大小(2)由得知质点的换向时刻为(t＝0不合题意)则所以,质点在4.0s时间间隔内的路程为(3)t＝4.0s时1-7　一质点沿x轴方向作直线运动,其速度与时间的关系如图(a)所示．设t＝0时,x＝0．试根据已知的v-t图,画出a-t图以及x-t图．14/14\n分析　根据加速度的定义可知,在直线运动中v-t曲线的斜率为加速度的大小(图中AB、CD段斜率为定值,即匀变速直线运动；而线段BC的斜率为0,加速度为零,即匀速直线运动)．加速度为恒量,在a-t图上是平行于t轴的直线,由v-t图中求出各段的斜率,即可作出a-t图线．又由速度的定义可知,x-t曲线的斜率为速度的大小．因此,匀速直线运动所对应的x-t图应是一直线,而匀变速直线运动所对应的x–t图为t的二次曲线．根据各段时间内的运动方程x＝x(t),求出不同时刻t的位置x,采用描数据点的方法,可作出x-t图．解　将曲线分为AB、BC、CD三个过程,它们对应的加速度值分别为14/14\n　(匀加速直线运动)　　　　(匀速直线运动)　(匀减速直线运动)根据上述结果即可作出质点的a-t图［图(B)］．在匀变速直线运动中,有由此,可计算在0～2ｓ和4～6ｓ时间间隔内各时刻的位置分别为用描数据点的作图方法,由表中数据可作0～2ｓ和4～6ｓ时间内的x-t图．在2～4ｓ时间内,质点是作的匀速直线运动,其x-t图是斜率k＝20的一段直线［图(c)］．　　1-9　质点的运动方程为式中x,y的单位为m,t的单位为ｓ．试求：(1)初速度的大小和方向；(2)加速度的大小和方向．分析　由运动方程的分量式可分别求出速度、加速度的分量,再由运动合成算出速度和加速度的大小和方向．解　(1)速度的分量式为当t＝0时,vox＝-10m·ｓ-1,voy＝15m·ｓ-1,则初速度大小为设vo与x轴的夹角为α,则α＝123°41′(2)加速度的分量式为14/14\n,则加速度的大小为设a与x轴的夹角为β,则β＝-33°41′(或326°19′)1-10　一升降机以加速度1.22m·ｓ-2上升,当上升速度为2.44m·ｓ-1时,有一螺丝自升降机的天花板上松脱,天花板与升降机的底面相距2.74m．计算：(1)螺丝从天花板落到底面所需要的时间；(2)螺丝相对升降机外固定柱子的下降距离．分析　在升降机与螺丝之间有相对运动的情况下,一种处理方法是取地面为参考系,分别讨论升降机竖直向上的匀加速度运动和初速不为零的螺丝的自由落体运动,列出这两种运动在同一坐标系中的运动方程y1＝y1(t)和y2＝y2(t),并考虑它们相遇,即位矢相同这一条件,问题即可解；另一种方法是取升降机(或螺丝)为参考系,这时,螺丝(或升降机)相对它作匀加速运动,但是,此加速度应该是相对加速度．升降机厢的高度就是螺丝(或升降机)运动的路程．解1　(1)以地面为参考系,取如图所示的坐标系,升降机与螺丝的运动方程分别为当螺丝落至底面时,有y1＝y2,即(2)螺丝相对升降机外固定柱子下降的距离为解2　(1)以升降机为参考系,此时,螺丝相对它的加速度大小a′＝g＋a,螺丝落至底面时,有(2)由于升降机在t时间内上升的高度为14/14\n则1-12　地面上垂直竖立一高20.0m的旗杆,已知正午时分太阳在旗杆的正上方,求在下午2∶00时,杆顶在地面上的影子的速度的大小．在何时刻杆影伸展至20.0m？分析　为求杆顶在地面上影子速度的大小,必须建立影长与时间的函数关系,即影子端点的位矢方程．根据几何关系,影长可通过太阳光线对地转动的角速度求得．由于运动的相对性,太阳光线对地转动的角速度也就是地球自转的角速度．这样,影子端点的位矢方程和速度均可求得．解　设太阳光线对地转动的角速度为ω,从正午时分开始计时,则杆的影长为s＝htgωt,下午2∶00时,杆顶在地面上影子的速度大小为当杆长等于影长时,即s＝h,则即为下午3∶00时．1-13　质点沿直线运动,加速度a＝4-t2,式中a的单位为m·ｓ-2,t的单位为ｓ．如果当t＝3ｓ时,x＝9m,v＝2m·ｓ-1,求质点的运动方程．分析　本题属于运动学第二类问题,即已知加速度求速度和运动方程,必须在给定条件下用积分方法解决．由和可得和．如a＝a(t)或v＝v(t),则可两边直接积分．如果a或v不是时间t的显函数,则应经过诸如分离变量或变量代换等数学操作后再做积分．解　由分析知,应有14/14\n得(1)由得(2)将t＝3ｓ时,x＝9m,v＝2m·ｓ-1代入(1)(2)得v0＝-1m·ｓ-1,x0＝0.75m．于是可得质点运动方程为1-15　一质点具有恒定加速度a＝6i＋4j,式中a的单位为m·ｓ-2．在t＝0时,其速度为零,位置矢量r0＝10mi．求：(1)在任意时刻的速度和位置矢量；(2)质点在Oxy平面上的轨迹方程,并画出轨迹的示意图．分析　与上两题不同处在于质点作平面曲线运动,根据叠加原理,求解时需根据加速度的两个分量ax和ay分别积分,从而得到运动方程r的两个分量式x(t)和y(t)．由于本题中质点加速度为恒矢量,故两次积分后所得运动方程为固定形式,即和,两个分运动均为匀变速直线运动．读者不妨自己验证一下．解　由加速度定义式,根据初始条件t0＝0时v0＝0,积分可得又由及初始条件t＝0时,r0＝(10m)i,积分可得由上述结果可得质点运动方程的分量式,即14/14\nx＝10＋3t2y＝2t2消去参数t,可得运动的轨迹方程3y＝2x-20m这是一个直线方程．直线斜率,α＝33°41′．轨迹如图所示．1-16　一质点在半径为R的圆周上以恒定的速率运动,质点由位置A运动到位置B,OA和OB所对的圆心角为Δθ．(1)试证位置A和B之间的平均加速度为；(2)当Δθ分别等于90°、30°、10°和1°时,平均加速度各为多少？并对结果加以讨论分析　瞬时加速度和平均加速度的物理含义不同,它们分别表示为和．在匀速率圆周运动中,它们的大小分别为,,式中｜Δv｜可由图(B)中的几何关系得到,而Δt可由转过的角度Δθ求出．由计算结果能清楚地看到两者之间的关系,即瞬时加速度是平均加速度在Δt→0时的极限值．解　(1)由图(b)可看到Δv＝v2-v1,故14/14\n而所以(2)将Δθ＝90°,30°,10°,1°分别代入上式,得,,以上结果表明,当Δθ→0时,匀速率圆周运动的平均加速度趋近于一极限值,该值即为法向加速度．1-18　飞机以100m·ｓ-1的速度沿水平直线飞行,在离地面高为100m时,驾驶员要把物品空投到前方某一地面目标处,问：(1)此时目标在飞机正下方位置的前面多远？(2)投放物品时,驾驶员看目标的视线和水平线成何角度？(3)物品投出2.0ｓ后,它的法向加速度和切向加速度各为多少？分析　物品空投后作平抛运动．忽略空气阻力的条件下,由运动独立性原理知,物品在空中沿水平方向作匀速直线运动,在竖直方向作自由落体运动．到达地面目标时,两方向上运动时间是相同的．因此,分别列出其运动方程,运用时间相等的条件,即可求解．此外,平抛物体在运动过程中只存在竖直向下的重力加速度．为求特定时刻t时物体的切向加速度和法向加速度,只需求出该时刻它们与重力加速度之间的夹角α或β．由图可知,在特定时刻t,物体的切向加速度和水平线之间的夹角α,可由此时刻的两速度分量vx、vy14/14\n求出,这样,也就可将重力加速度g的切向和法向分量求得．解　(1)取如图所示的坐标,物品下落时在水平和竖直方向的运动方程分别为x＝vt,　y＝1/2gt2飞机水平飞行速度v＝100m·s-1,飞机离地面的高度y＝100m,由上述两式可得目标在飞机正下方前的距离(2)视线和水平线的夹角为(3)在任意时刻物品的速度与水平轴的夹角为取自然坐标,物品在抛出2s时,重力加速度的切向分量与法向分量分别为1-19　如图(a)所示,一小型迫击炮架设在一斜坡的底端O处,已知斜坡倾角为α,炮身与斜坡的夹角为β,炮弹的出口速度为v0,忽略空气阻力．求：(1)炮弹落地点P与点O的距离OP；(2)欲使炮弹能垂直击中坡面．证明α和β必须满足并与v0无关．分析　这是一个斜上抛运动,看似简单,但针对题目所问,如不能灵活运用叠加原理,建立一个恰当的坐标系,将运动分解的话,求解起来并不容易．现建立如图(a)所示坐标系,则炮弹在x和y两个方向的分运动均为匀减速直线运动,其初速度分别为v0cosβ和v0sinβ,其加速度分别为gsinα和gcosα．在此坐标系中炮弹落地时,应有y＝0,则x＝OP．如欲使炮弹垂直击中坡面,则应满足vx＝0,直接列出有关运动方程和速度方程,即可求解．由于本题中加速度g为恒矢量．故第一问也可由运动方程的矢量式计算,即,做出炮弹落地时的矢量图［如图(B)所示］,由图中所示几何关系也可求得(即图中的r矢量)．14/14\n(1)解1　由分析知,炮弹在图(a)所示坐标系中两个分运动方程为(1)(2)令y＝0求得时间t后再代入式(1)得解2　做出炮弹的运动矢量图,如图(b)所示,并利用正弦定理,有从中消去t后也可得到同样结果．(2)由分析知,如炮弹垂直击中坡面应满足y＝0和vx＝0,则(3)由(2)(3)两式消去t后得由此可知．只要角α和β满足上式,炮弹就能垂直击中坡面,而与v0的大小无关．讨论　如将炮弹的运动按水平和竖直两个方向分解,求解本题将会比较困难,有兴趣读者不妨自己体验一下．1-20　一直立的雨伞,张开后其边缘圆周的半径为R,离地面的高度为h,(1)当伞绕伞柄以匀角速ω旋转时,求证水滴沿边缘飞出后落在地面上半径为的圆周上；(2)读者能否由此定性构想一种草坪上或农田灌溉用的旋转式洒水器的方案？14/14\n分析　选定伞边缘O处的雨滴为研究对象,当伞以角速度ω旋转时,雨滴将以速度v沿切线方向飞出,并作平抛运动．建立如图(a)所示坐标系,列出雨滴的运动方程并考虑图中所示几何关系,即可求证．由此可以想像如果让水从一个旋转的有很多小孔的喷头中飞出,从不同小孔中飞出的水滴将会落在半径不同的圆周上,为保证均匀喷洒对喷头上小孔的分布还要给予精心的考虑．解　(1)如图(a)所示坐标系中,雨滴落地的运动方程为(1)(2)由式(1)(2)可得由图(a)所示几何关系得雨滴落地处圆周的半径为(2)常用草坪喷水器采用如图(b)所示的球面喷头(θ0＝45°)其上有大量小孔．喷头旋转时,水滴以初速度v0从各个小孔中喷出,并作斜上抛运动,通常喷头表面基本上与草坪处在同一水平面上．则以φ角喷射的水柱射程为为使喷头周围的草坪能被均匀喷洒,喷头上的小孔数不但很多,而且还不能均匀分布,这是喷头设计中的一个关键问题．1-21　一足球运动员在正对球门前25.0m处以20.0m·ｓ-1的初速率罚任意球,已知球门高为3.44m．若要在垂直于球门的竖直平面内将足球直接踢进球门,问他应在与地面成什么角度的范围内踢出足球？(足球可视为质点)14/14\n分析　被踢出后的足球,在空中作斜抛运动,其轨迹方程可由质点在竖直平面内的运动方程得到．由于水平距离x已知,球门高度又限定了在y方向的范围,故只需将x、y值代入即可求出．解　取图示坐标系Oxy,由运动方程,　消去t得轨迹方程以x＝25.0m,v＝20.0m·ｓ-1及3.44m≥y≥0代入后,可解得71．11°≥θ1≥69．92°27．92°≥θ2≥18．89°如何理解上述角度的范围？在初速一定的条件下,球击中球门底线或球门上缘都将对应有两个不同的投射倾角(如图所示)．如果以θ＞71．11°或θ＜18.89°踢出足球,都将因射程不足而不能直接射入球门；由于球门高度的限制,θ角也并非能取71.11°与18.89°之间的任何值．当倾角取值为27.92°＜θ＜69．92°时,踢出的足球将越过门缘而离去,这时球也不能射入球门．因此可取的角度范围只能是解中的结果．1-22　一质点沿半径为R的圆周按规律运动,v0、b都是常量．(1)求t时刻质点的总加速度；(2)t为何值时总加速度在数值上等于b？(3)当加速度达到b时,质点已沿圆周运行了多少圈？分析　在自然坐标中,s表示圆周上从某一点开始的曲线坐标．由给定的运动方程s＝s(t),对时间t求一阶、二阶导数,即是沿曲线运动的速度v和加速度的切向分量aｔ,而加速度的法向分量为an＝v2/R．这样,总加速度为a＝aｔeｔ＋anen．至于质点在t时间内通过的路程,即为曲线坐标的改变量Δs＝st-s0．因圆周长为2πR,质点所转过的圈数自然可求得．14/14\n解　(1)质点作圆周运动的速率为其加速度的切向分量和法向分量分别为,故加速度的大小为其方向与切线之间的夹角为(2)要使｜a｜＝b,由可得(3)从t＝0开始到t＝v0/b时,质点经过的路程为因此质点运行的圈数为14/14