大学物理综合

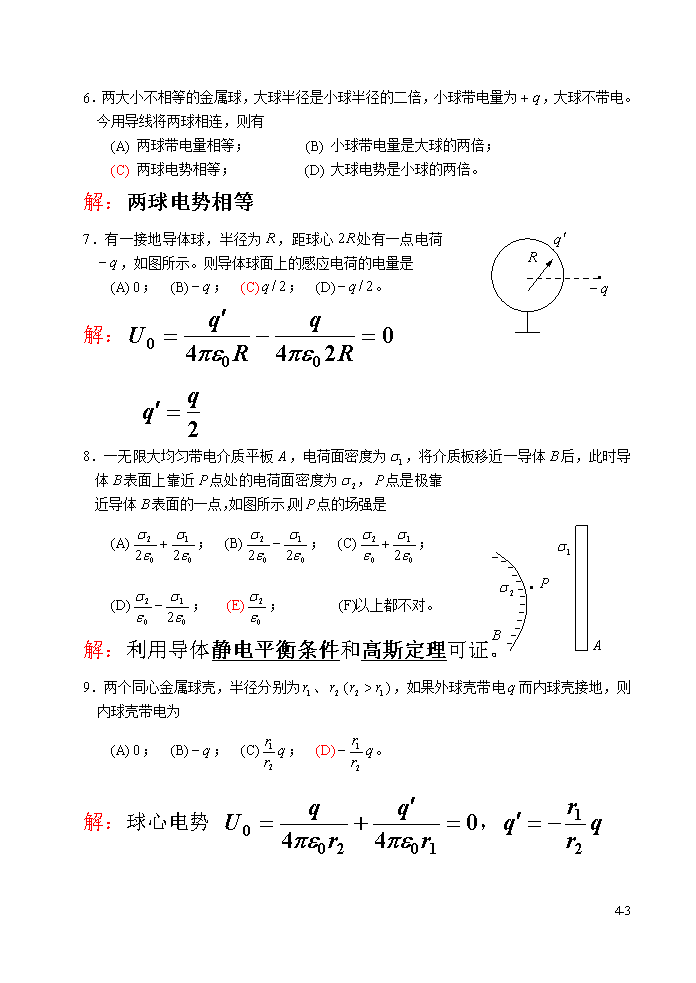
大学物理综合

《大学物理》综合练习(四)——静电学教学班级：序号：姓名：日期： 一、选择题(把正确答案的序号填入括号内)1．两个电量都是的点电荷相距，为其连线的中点，如图所示。则其中垂线轴上，场强取极大值的点到点的距离为(A)；(B)；(C)；(D)。解：，，2．真空中两带电平行板、，板间距为（很小），板面积为，带电量分别为和。若忽略边缘效应，则两板间作用力的大小为(A)；(B)；(C)；(D)。解：，3．如图，、是真空中两块相互平行的均匀带电平面，电荷面密度分别为和，若板选作零电势参考点，则图中点的电势是(A)；(B)；(C)；(D)。4-17\n解：•〇〇〇〇++--4．四个点电荷的电量相等，两正两负置于正方形的四角上，如图所示。令和分别为图示中心处的电势和场强的大小，当仅有左上角的点电荷存在时，点处的电势和场强分别为和，试问和的值为多少?(A)，；(B)，；(C)，；(D)，。解：•5．如图所示，在相距的点电荷和的电场中，把点电荷从点沿移到点，则电场力作功与(系统)电势能的增量分别为•(A)，；(B)，；(C)，；(D)，。解：4-17\n6．两大小不相等的金属球，大球半径是小球半径的二倍，小球带电量为，大球不带电。今用导线将两球相连，则有(A)两球带电量相等；(B)小球带电量是大球的两倍；(C)两球电势相等；(D)大球电势是小球的两倍。解：两球电势相等•7．有一接地导体球，半径为，距球心处有一点电荷，如图所示。则导体球面上的感应电荷的电量是(A)；(B)；(C)；(D)。解：•8．一无限大均匀带电介质平板，电荷面密度为，将介质板移近一导体后，此时导体表面上靠近点处的电荷面密度为，点是极靠近导体表面的一点，如图所示，则点的场强是(A)；(B)；(C)；(D)；(E)；(F)以上都不对。解：利用导体静电平衡条件和高斯定理可证。9．两个同心金属球壳，半径分别为、，如果外球壳带电而内球壳接地，则内球壳带电为(A)；(B)；(C)；(D)。解：球心电势，4-17\n••••10．如图所示，一个封闭的空心导体，观察者(测量仪器)和电荷置于导体内，而观察者和电荷置于导体外，下列说法中哪一种是正确的(A)只观察到产生的场，只观察到产生的场；(B)可观察到和产生的场，只观察到产生的场；(C)只观察到产生的场，可观察到和产生的场。解：导体空腔外的电荷对导体腔内的电场及电荷分布没有影响，只观察到产生的场；通过在腔外表面感应出等量同号电荷影响外电场，可观察到和产生的场。11．密度均匀的电荷分布在半径为的球内，其总电量为，则系统的总静电能为(A)；(B)；(C)；(D)解：利用高斯定理：；：，12．一个半径为的金属球带有正电荷，球外包围着一层同心的相对介电常数为的均匀电介质球壳层，其内半径为，外半径为，在电介质内的点距离球心为，则点的电势为(A)；(B)；4-17\n(C)；(D)。解：由高斯定理：；：••二、填充题(单位制为SI)1．如图所示，两个点电荷与位于坐标轴上，已知两电荷间距离为，点到的距离为，则点的场强，其中；。解：，，，4-17\n2．一无限长带电圆柱体，半径为，其电荷体密度，为常数，为轴线到场点的距离，则带电圆柱所产生的场强分布在圆柱体外为；在圆柱体内为。解：利用高斯定理，做半径为，长为的圆柱形高斯面：：•••3．把单位正电荷从一对等量异号电荷连线中点，沿任意路线移到无穷远处，则电场力对该单位正电荷所作的功为0。解：4-17\n或•++++++++++++++4．长度为的细玻璃棒，沿着长度方向均匀地分布着电荷，总电量为，如图所示。在棒的轴向有一点，离棒左端的距离为，则点的电势。•••解：5．如图所示，有一半径为的均匀带电圆环，带电量为，其轴线上有两点和，。设无穷远处的电势为零，、两点的电势分别为和，则。解：4-17\n6．接第5题，把电荷从点移到点，外力作的功。解：电场力的功外力作功•••7．在带电量为的导体球外部有一相对介电常数为的电介质球壳，在电介质内外分别为有两点、，它们到球心的距离为和，则；；；。解：利用、的高斯定理及、关系求解。•o••••8．两带电量皆为的点电荷相距，一接地的半径为的导体球置于它们中间，如图所示。则导体球所带的净电量；若去掉接地线，把导体球充电到电势，则导体球所带净电量。4-17\n解：，，9．有一固定不动半径为的导体薄球壳，带电量为，在薄球壳的正上方到球心的距离为的点放一点电荷，如图所示。则导体薄壳中心点的电势，导体薄球壳面上最高点的电势。解：10．如图所示，中性导体内有带电体、，外面有带电体、、……，今使、所带电量变化，则外的电场变化(变或不变)，电势变化(变或不变)；、、……电量变化，内的电场不变，内的电势变化。解：根据导体静电感应条件及屏蔽概念可解。4-17\n三、计算题不讲1．如图所示，一带电细线弯成半径为的圆环，电荷线密度为，式中为一常数，为半径与轴的夹角，试求环心处电场强度。解：在圆环上任取一段，到点的连线与轴夹角为，则段上的电荷在点产生场强的大小为的方向如图所示。，整个圆环上的电荷在点产生的场强为4-17\n不讲2．一半径为的带电球体，其电荷体密度，为正常数，为球心到球内一点的矢径的大小。求此带电球体所产生的电场强度的分布。解：在球体内，取半径为的球面为高斯面，所含电量由高斯定理得在球外，取半径为的球面为高斯面，所含电量4-17\n3．一圆盘，半径，均匀带电，而电荷面密度，求：(1)轴线上任一点的电势(用该点与盘心的距离表示)；(2)从电场强度和电势梯度的关系，求该点的电场强度；(3)计算的电势和场强。•解：(1)半径为、宽度为的窄圆环的带电量为此窄圆环在点产生的电势整个圆环在点产生的电势为(2)场强方向沿轴正向。(3)，，，4-17\n·P4321不讲4．有两个无限大平行平面带电导体板，如图所示。证明：(1)相向的两面上，电荷面密度总是大小相等而符号相反；(2)相背的两个面上，电荷面密度总是大小等而符号相同。解：(1)取两底面分别位于两导体板内部的柱面为高斯面，设底面面积为，则由高斯定理得面内包围电荷(2)在左导体内部场强为零，即各面上的电荷在其内产生的合场强为零即所以4-17\n5．半径为的导体球带有电荷，此球外有一个内、外半径为、的同心导体球壳，壳上带有电荷，如图所示。•(1)求球的电势，球壳的电势及其电势差；(2)用导线把内球和外球壳的内表面联结在一起后，、和各为多少?(3)在情况(1)中，若外球接地，、和又各为多少?(4)在情况(1)中，设外球离地面很远，若内球接地，情况又怎样?解：(1)由于静电感应，球壳内表面应带电，外表面带电。内球电势或外球电势两球间的电势差4-17\n(2)连接后(3)外球接地，则(4)内球接地，则，设此时内球剩余电荷为，由于静电感应，外球壳内外表面分别带电和所以4-17\n6．在半径为长为的均匀带电金属棒外，同轴地包围一层内、外半径分别为、的圆柱形均匀电介质壳层，其相对介电常数为，金属棒上轴向每单位长度的电荷为，设，试求(1)电场强度的分布；(2)若规定金属棒的电势为零，求电介质外表面的电势；(3)电介质内的电场能量。解：因，忽略两端的边缘效应，带电金属棒可视为无限长。(1)场强分布(导体内部)：；：；：；4-17\n：。(2)，介质外表面电势(3)介质内的电场能量4-17