《大学物理》课件

《大学物理》课件

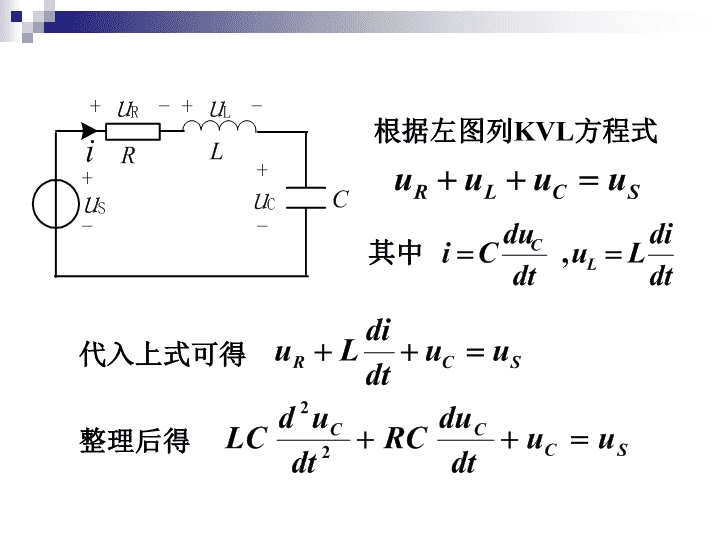
第七章动态电路的时域分析讨论可以用一阶微分方程描述的电路。介绍一阶电路的经典法及时间常数的概念。直流激励作用下一阶电路零输入响应、零状态响应、全响应、阶跃响应、冲激响应的概念及其求解。\n§7－1动态电路的方程及其初始条件1.工作状态：一、概念稳定工作状态（稳态）过渡工作状态（暂态）直流稳态正弦稳态非正弦周期稳态2.稳态：电压或电流随时间恒定不变或作周期性变化。3.暂态：例如火车的加速过程等。4.动态元件：电容元件和电感元件的电压、电流的约束关系是通过导数（或积分）表达的，称为动态元件\n根据左图列KVL方程式其中代入上式可得整理后得\n5.换路：参数的改变（如电阻的变大、变小）、电源的变化、电路的开通和关断都可以看作是支路的接通和扳断，在电路中称为“换路”。计时的起点为t=0（认为换路是在t=0时刻进行的）。t=0-（换路前的终了时刻）；t=0+（换路后的起始时刻），0-和0+是0的左右两个极限，认为换路是瞬间完成的，时间间隔是0。6.过渡过程：电路发生“换路”时，使电路由原工作状态转变到另一种工作状态，这种转变往往经历一个过程，在工程上称为过渡过程。\n二、工作状态1.工作状态：储能状态。已知即储能状态取决于uC(t)和iL(t)，所以把某一时刻uC(t)和iL(t)称为状态变量。2.换路定则(1)原始工作状态为uC(0-)，iL(0-)；初始工作状态为uC(0+)，iL(0+)uC(0+)=uC(0-)iL(0+)=iL(0-)有且uL，iC必须为有限值\n(2)因为若令t=0+，则当iC为有限值时，即电容电压不能跃变，而应连续变化。(3)同理若令t0=0-，t=0+，则即电感电流不能跃变，而应连续变化。\n3.初始条件(1)独立初始条件（符合换路定律）：包括独立电容的电压uC(0+)，独立电感的电流iL(0+)。(2)非独立初始条件：电阻的电压或电流、电容电流、电感电压等需通过已知的独立初始条件求得的量就是非独立初始条件。4.由替代定理可知：对于t=0+时刻的等效电路uC(0+)=uC(0-)相当于电压源iL(0+)=iL(0-)相当于电流源\n解：可以根据t=0-时刻的电路状态计算uC(0-)和uL(0-)。由于开关打开前，电路中的电压和电流已恒定不变，所以电容电流和电感电压均为零，即此时的电容相当于开路，电感相当于短路。5.举例说明例：图(a)所示，当电路中的电压和电流恒定不变时打开开关S。试求uC(0+)、iL(0+)、iC(0+)、uL(0+)、iR(0+)和。\n且有作出t=0+时刻的等效电路，如图(c)所示。其中将已知的uC(0+)和iL(0+)分别以6V电压源和2A电流源替代。t=0-时刻，等效电路如图(b)所示\nt=0+时刻，等效电路如图(c)所示由KVL有\n解题步骤：计算出换路前的uC(0-)和iL(0-)。电容开路，电感短路(2)作t=0+时刻的等效电路，按照换路定律uC(0+)=uC(0-)，iL(0+)=iL(0-)电容用电压为uC(0+)电压源替代，电感用iL(0+)电流源替代。若有独立源uS(t)，则变成uS(0+)(3)解此直流电路，解出非独立的初始条件。\n6.阶数：含有一个独立储能元件的电路，电路的输入输出方程为一阶微分方程，相应的电路为一阶电路。一阶电路一阶电路二阶电路\n§7－2一阶电路的零输入响应1.RC电路一、RC一阶电路的零输入响应因为所以图(a)换路后的电路如图(b)所示。则有图(b)即整理可得\n令通解代入上式得特征方程所以将p代入uC中，得到图(b)方程又因为故A=U0。所以\n2.时间常数从上表可以看出，的大小反映了一阶电路过渡过程的进展速度，是反映过渡过程特性的一个重要的量。(1)经过时刻，uC()=0.368U0。(2)工程上认为3~5时间放电结束。(3)通过调整RC来调整（越大，放电时间越长；越小，放电时间越短）。逐渐减小单位为：\n(4)时间常数的几何意义（时间坐标上次切距的长度等于）。左图中，取电容电压uC的曲线上任意一点A，通过A点作切线AC，则图中的次切距\n(5)时间常数的计算3.电容通过电阻放电的能量变化过程：左图为一换路后的零输入电路，则电路的时间常数为\n例：图(a)所示电路开关S原在位置1，且电路已达稳态。t=0时开关由1合向2，试求t≥0时的电流i(t)。图(a)解：首先求出换路后，电路如图(b)所示图(b)\n电容通过电阻R1、R2放电，由于R1、R2为并联，设等效电阻为R3，则有：所以图(b)\n二、RL一阶电路的零输入响应1.RL电路图(a)因为换路后的电路如图(b)所示。则有所以所以图(b)\n令通解代入上式得特征方程所以将p代入iL中，得到又因为故A=I0。所以t≥0+令RL电路的时间常数图(b)方程\nt≥0+所以t≥0+t≥0+物理过程：电感通过电阻消磁过程（不能太快）。图(b)\n2.例题：下图所示是一台300kW汽轮发电机组的励磁回路。已知励磁绕阻的电阻R=0.189，电感L=0.398H，直流电压U=35V。电压表的量程为50V，内阻RV=5K。开关未断开时，电路中电流已经恒定不变。在t=0时，断开开关。求：(1)电阻、电感回路的时间常数；(2)电流i的初始值和开关断开后电流i的最终值；(3)电流i和电压表处的电压uV；(4)开关刚断开时，电压表处的电压。解：(1)时间常数\n(2)开关断开前，由于电流已恒定不变，电感两端电压为零，故由于电感中电流不能跃变，电流的初始值开关断开后，电感通过电阻消磁，所以电流的终值为0(3)按可得电压表处的电压\n(4)开关刚断开，电压表处的电压由此可见，开关刚断开时电压表处的电压很大，其绝对值远大于直流电源的电压U，而且初始瞬间的电流也很大，可能损坏电压表。因此，切断电感电流时，必须考虑磁场能量的释放。如果磁场能量较大，而又必须在短时间内完成电流的切换，则必须考虑如何熄灭因此而出现的电弧的问题。\n如图(a)所示电路，已知iL(0+)=150mA，求t>0时的电压u(t)解:先求电感两端的等效电阻Req。采用外加电源法，如图(b)所示。由KVL得\n换路后的等效电路如图(c)所示，则\n§7－3一阶电路的零状态响应1.RC电路一、RC一阶电路在直流激励下的零态响应因为又因为代入可得所以，有故（非齐次方程的）特解（齐次方程的通解）补充函数方程通解：\n故A=-US。因此所以又有所以t≥0+\n画uC、i的波形根据t≥0+\n3.分析(1)特解uC’与外加激励的变化规律有关，又称强制分量(2)通解uC’’的变化规律与外加激励无关，又称为自由分量即(3)自由分量又称为暂态分量；但只在直流输入、正弦输入、周期激励输入下，强制分量才称为稳态分量。2.电压转移，通过电阻转移到电容上。\n1.RL电路二、RL一阶电路在直流激励下的零态响应因为又有代入可得所以，有故所以所以\n§7－4一阶电路的全响应1.RC电路设开关S闭合后，根据KVL有故A=U0-US因为所以t≥0+初始条件方程的通解\n2.零输入响应零状态响应说明：全响应是零输入响应和各个独立源单独作用的零态响应的叠加，是线性电路叠加原理的体现。画u、i的波形根据t≥0+\n3.(1)在直流激励下，将f’(t)记作f()（终值），故(2)t=0+时，初值f(0+)=f()+A，所以A=f(0+)-f()，故(3)因此，只要知道初值f(0+)、终值f()和共同的时间常数，就可以求出f(t)，这种方法被称为三要素法。(4)在正弦激励下其中：f’(t)是特解，f’(0+)是t=0+时刻稳态响应的初始值，f(0+)是初始值，是时间常数。\n例：图(a)所示电路中，US=10V，IS=2A，R=2，L=4H。试求S闭合后电路中的电流iL和i。图(a)解：图(a)开关闭合后的戴维宁等效电路如图(b)所示，其中：图(b)根据图(b)，可以观察到\n根据三要素法列式，可得：t≥0+求得：t>0时间常数图(b)\n例：电路如图(a)所示，试求S闭合后电路中的电流i。图(a)解：(1)(3)(2)作出t=0+时刻的等效电路，如图(b)所示图(b)易求得\n(4)图(c)所示，将独立源置零，从电感端口向外看，可看出三个电阻为并联，故(5)根据三要素法列式，可得：图(c)t>0\n§7－5一阶电路的阶跃响应1.单位阶跃函数一、定义2.延迟单位阶跃函数：时刻起始的阶跃函数(t-)。3.延迟阶跃函数：A(t-)。\n2.单位阶跃函数用来“起始”任意某个函数f(t)。：用(t)来起始函数二、作用1.表示开关的动作已知uC(0-)=0\n3.用来表示一个阶梯波形。\n三、单位阶跃响应单位阶跃激励源作用下产生的零态响应，称作单位阶跃响应，用S(t)表示。例：已知电路如图所示，求单位阶跃响应S(t)。单位阶跃响应：电路零态响应：已知电路的S(t)，如果该电路的激励为则电路的零态响应为U0S(t)。\n例：下图(a)所示电路中，开关S合在位置1时电路已达稳定状态。t=0时，开关由位置1合向位置2，在t==RC时，又由位置2合向位置1，求t≥0时的电容电压uC(t)。解法一：图(a)0≤t<时的电路如图(b)所示。图(b)方程的解为列方程（零状态）\nt>时的电路如图(c)所示。图(c)列方程方程的解为：图(a)（零输入）\n解法二：（激励源分成两个阶跃源的叠加。）电容电压可看作两个零态方程，但起始时间不同，故有验证：(1)0≤t<时(2)t>时图(a)\n§7－6一阶电路的冲激响应1.单位冲激函数一、定义2.实际上可以用筛分性质表示：单位矩形脉冲函数f(t)的波形，高为1/，宽为，面积为1\n三角形函数f(t)的波形，高为1/，宽为2，面积为1。3.延迟冲激函数：延迟冲激函数k(t-2)冲激强度为k延迟冲激函数(t-1)冲激度为1单位冲激函数(t)冲激度为1\n二、性质1.单位冲激函数(t)对时间的积分等于单位阶跃函数(t)，即反之，阶跃函数(t)对时间的一阶导数冲激函数(t)，即\n证明：(1)当0时，f(t)(t)，f’(t)(t)所以(2)因为且有因为它们定义相同，所以\n2.筛分性质：对于任意在t=0时连续的函数f(t)，将有因此同理图(a)例：已知电路如图(a)所示，求开关S闭合后，电流iC=？解：直接求解不容易。观察电路图(b)。\n而即在0-0+期间，1F电容上的电压达到1V。对于图(a)来说，S闭合瞬间，1F电容上的电压达到1V，故电流iC=(t)。对于图(b)来说，S闭合后的电流为图(b)图(a)\n3.(t)激励下的RC电路已知电路如图所示，求冲激响应uC、iC和iR。解：(1)0-0+时即对上式两边同时积分，得整理后，可得因此所以（冲激函数的作用使电容电压跃变。）\n(2)t>0+时因为此时(t)=0，所以因此u、i的波形\n4.(t)激励下的RL电路已知电路如图所示，求冲激响应uR、uL和iL。即对上式两边同时积分，得解：(1)0-0+时整理后，可得因此所以\n(2)t>0+时因为此时(t)=0，所以因此或\n5.(1)线性、非时变电路的冲激响应h(t)和阶跃响应s(t)之间有如下重要关系：(2)证明：按照冲激函数的定义，有：对于一个线性电路，描述电路性状的微分方程为线性常系数方程。对于这种电路，如设激励为e(t)时的响应为r(t)，则当所加激励为e(t)的导数或积分时，所得响应必相应地为r(t)的导数或积分。冲激激励是阶跃激励的一阶导数，因此冲激响应可以按照阶跃响应的一阶导数求得。\n输入响应输入响应\n\n6.举例说明利用求导从一个量得到另一个量时，求导时必须将(t)带入运算。因为(t)只存在t=0时，而此时e0=1，因此例：已知图(a)所示电路中，iL(0-)=0，R1=6，R2=4，L=100mH，求冲激响应iL和uL。图(a)\n图(a)解：首先将电感L以外的电路用戴维宁定理等效变换为如图(b)电路所示。图(b)其中根据KVL有对方程两边0-至0+积分得\n整理后，可得所以因此图(b)