大学物理练习
nA大学物理(磁学)试卷班级:姓名:学号:R期:年月Fl成绩:一选择题(共24分)1(本题3分)在磁感强度为B的均匀磁场中作一半径为r的半球面S,S边线所在平面的法线方向单位矢量巨与B的夹角为a,则通过半球面S的磁通量(取弯面向外为正)为(A)nrB..(B)2jt/B.(C)~nr2Bsina.(D)-nr1Bcosa.2(本题3分)电流I由长直导线1沿垂直be边方向经a点流入由电阻均匀的导线构成的正三角形线框,再由b点流出,经长直导线2沿必延长线方向返回电源(如图).若载流直导线」、2—和三角形框中的电流在框中心0点产生的磁感强度分别用岔、和凤表示,则0点的磁感强度大小(A)B=0,因为Bi=B2=B3=O.(B)B=0,因为虽然0、禺工0,但岔+凤=0,^=0.(C)BH0,因为虽然B3=0、Bi=0,但勺工0.(D)3H0,因为虽然£+艮工0,但艮工0.[3(本题3分)磁场山沿空心长圆筒形导体的均匀分布的电流产生,圆筒半径为R,兀坐标轴垂直圆筒轴线,原点在中心轴线上.图(A)〜(E)哪一条曲线表示B-x的关系?[B]4(本题3分)如图所示,在磁感强度为D的均匀磁场中,冇一圆形载流导线,a、b、c是其上三个长度相等的电流元,则它们所受安培力大小的关系为\n(A)Fa>Fh>F-(B)Fa
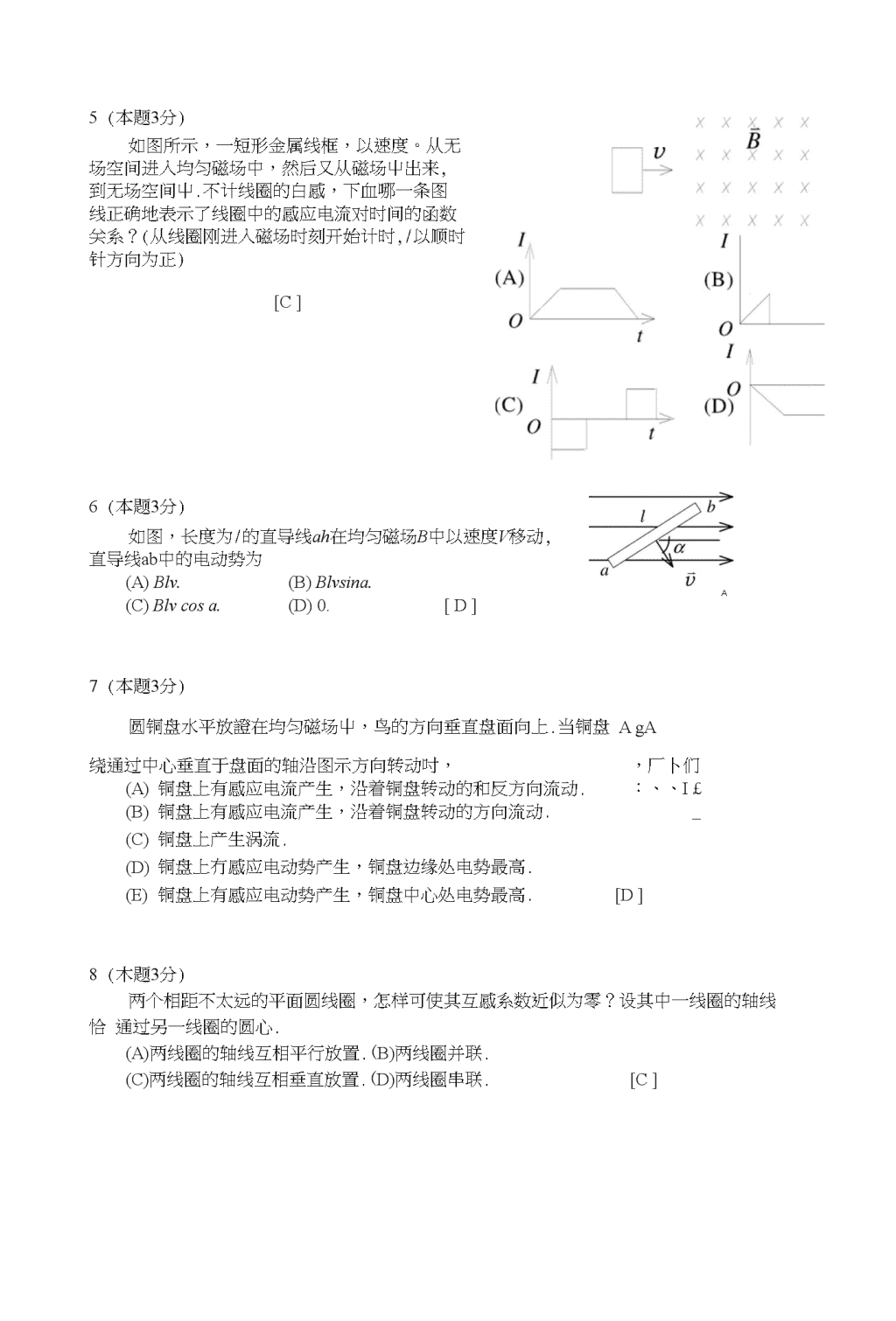
Fe>Fa.(D)Fa>Fc>Fh.\n2(本题3分)如图所示,一短形金属线框,以速度。从无场空间进入均匀磁场中,然后又从磁场屮出来,到无场空间屮.不计线圈的白感,下血哪一条图线正确地表示了线圈中的感应电流对时间的函数关系?(从线圈刚进入磁场时刻开始计时,/以顺时针方向为正)[C]3(本题3分)如图,长度为/的直导线ah在均匀磁场B中以速度V移动,直导线ab中的电动势为(A)Blv.(B)Blvsina.(C)Blvcosa.(D)0.[D]A4(本题3分)圆铜盘水平放證在均匀磁场屮,鸟的方向垂直盘面向上.当铜盘AgA绕通过中心垂直于盘面的轴沿图示方向转动吋,,厂卜们(A)铜盘上有感应电流产生,沿着铜盘转动的和反方向流动.:、、I£(B)铜盘上有感应电流产生,沿着铜盘转动的方向流动._(C)铜盘上产生涡流.(D)铜盘上冇感应电动势产生,铜盘边缘处电势最高.(E)铜盘上有感应电动势产生,铜盘中心处电势最高.[D]5(木题3分)两个相距不太远的平面圆线圈,怎样可使其互感系数近似为零?设其中一线圈的轴线恰通过另一线圈的圆心.(A)两线圈的轴线互相平行放置.(B)两线圈并联.(C)两线圈的轴线互相垂直放置.(D)两线圈串联.[C]\n二填空题(共24分)2(本题3分)一半径为a的无限长直载流导线,沿轴向均匀地流有电流/.若作一个半径为R=5a、高为/的柱形曲而,已知此柱形曲而的轴与载流导线的轴平行且相距3d(如图).则P在圆柱侧面S上的积分Jp・d5=03(本题3分)载有电流/的导线由两根半无限长有导线和半径为R的、以兀)忆朋标系原点O为中心的3/4圆弧组成,圆弧在乙平面内,两根半无限长直导线与x轴平行,电流流向如图所示.O点的磁感强度(用坐标轴正方向单位矢量i,j,k表示)4(本题4分)如图,平行的无限长肓载流导线A和B,电流强度均为/,垂宜纸面向外,两根载流导线Z间相距为Q,则(1)而中点(P点)的磁感强度乞=0.(2)磁感强度P沿图小环路厶的线积分jB-dl=-Ao/•LA.V5(本题3分)流导线加所受的磁力大小为—41aJBXXXX如图所示,在真空屮有一半径为。的3/4圆弧形的导线,其屮通以稳恒电流/,导线遥于均匀外磁场鸟中,RD与导线所在平面垂直.则该载\n2(本题4分)判断在下述情况下,线圈屮有无感应电流,若有,在图中标明感应电流的方向.(1)两圆环形导体互相垂直地放置•两环的中心重合,口彼此绝缘,当B环中的电流发生变化吋,在A环中无感应电流•(2)无限长载流直导线处在导体圆环所在平而并通过环的中心,载流直导线与圆环互相绝缘,当圆环以肓导线为轴匀速转动时,圆环屮—无感应电流—•XXXXXXX3(木题4分)半径为L的均匀导岁圆盘绕通过中心0的垂直轴转动,角速度为。盘面与均匀磁场P垂直,如图.(1)图上0。线段中动生电动势的方向为段电动势方向由d指向⑵填写下列电势差的值(设g段长度为d):1.Ua—U()=-—BcoIj•2u(—uh=0-Ua—Uc=coBd(2L—d)215(本题分3)真空中两只长直螺线管1和2,长度相等,单层密绕匝数相同,直径之比di/J2=l/4.当它们通以相同电流吋,两螺线管贮存的磁能Z比为W|/W2=_l:16—•参考答案:B=我丿初d:2Ao2”。4巴=+“0〃2厂/兀(盃/4)叱:吧=d::d;=1:16\n三计算题(共47分)16(木题5分)一根无限长导线弯成如图形状,设各线段都在同一平面内(纸而内),其中第二段是半径为R的四分之一圆弧,其余为直线.导线中通冇电流/,求图中。点处的磁感强度.解:将导线分成1、2、3、4四部份,各部分在0点产牛•的磁感强度设为Bi、B2、B3、&•根据叠加原理。点的磁感强度为:B+艮++B-•・•&、P斗均为0,故B=B2+B31分禺弓船方向0B3=^-(sin02_sin0J=["24g4k/?=XZ0//(2k/?)方向®其中a=R丨近,sin02=sin(兀/4)=血/2sin0]=sin(-7i/4)=-V2/2・・・_型*丛J如丄+丄方向08/?2兀R2R47t17(本题12分)两个无穷大平行平而上都有均匀分布的而电流,而电流密度分别为h和4若力和也之间夹角为&,如图,求:(1)两血之间的磁感强度的值(2)两面Z外空间的磁感强度的值(3)当ix=i2=f,0=0时以上结果如何?解:当只有一块无穷大平而存在时,利用安培环路定理,可知板外的磁感强度值为现有两块无穷人平面,&与石夹角为&,因$丄,场丄■,故$和爲夹角也为&或兀D_1•-0.(1)在两面2间£和场夹角为(兀—&)故B,二+〃o(岸+岸一2讹2COS0)"(2)在两面之外E和直2的夹角为&,故6=*心(『+岸+2花心&严当z\=i2=i,&=0时,有2分2分2分2分Bj=_a/2//qZVl—cos0—0\n16(本题5分)如图所示,有两根平行放置的长直载流导线.它们的直径为反向流过相同大小的电流h电流在导线内均匀分布.试在图示的坐标系屮求出X轴上两导线之间区域[丄丄加内磁感强度的分布.12解:应用安培环路定理和磁场叠加原理可得磁场分布为,B”%化虫爲)2tzx2n(3a-x)22片的方向垂直x轴及图而向里.17(本题5分)通有电流I的长直导线在一平而内被弯成如图形状,放于垂直进入纸面的均匀磁场B'P,求整个导线所受的安培力(R为已知).解:长直导线AC和3D受力大小相等,方向相反H.在同一直线上,故合力为零•现计算半圆部分受力,取电流元血,dF=/(lixB即dF=//?Bd&2分由于对称性n:.F=Fv=JdFv=^IRBsmOAd=2RIB3分v0方向沿y轴正向18(本题10分)如图所示,两条平行长直导线和一个矩形导线框共而.且导线框的一个边与长直导线平行,他到两长直导线的距离分别为厂I、r2.已知两导线中电流都为I=/0sincot,其中/o和0为帘数,/为时间.导线櫃长为。宽为b,求导线框屮的感应电动势.解:两个载同向电流的长肓导线在如图坐标兀处所产生的磁场为召=牛(丄+—!—)2kxx—斤+厂2选顺时针方向为线框回路止方向,则丛]n(P2兀r.r2J2k*x*%-rf+/2XdO二“腔1詁打+/?)r+b)]d/dr27tr\r2dt\n"。加备[血如型]cos必21(本题10分)载有电流的/长直导线附近,放一导体半圆环MeN与长直导线共面,且端点MN的连线与长直导线垂直•半圆环的半径为4心。与导线相距G.设半圆环以速度方平行导线平移,求半圆感应电动势的人小和方向以及MN两端的电压UM-U科.NJ(vxB)-drMN为计算简单,可引入一条辅助线MN,构成闭合回路M&NM,闭合回路总电动势%、-eMeN+£NM~°£MeN=~£NM-$alb2tlx2兀a-b解:动生电动势认XMN£~J(vxB)-df=MN负号表示®册的方向与X轴相反.稠-2tta-b方向N—MTJTT—e一“()"h°“四回答问题(共5分)22(本题5分)用简单例了说明:楞次定律是能量守恒的必然结果.换句话说,如果电磁感应的规律正好与楞次定律相反,则能量守恒定律便不成立.答:例如在磁棒靠近线圈时,线圈小产生感应电流,按楞次定律,线圈电流方向应如图所示,这样线圈阻碍磁棒靠近,使磁棒的动能转化为线圈的磁场能和线圈中因冇电流而生的热.2分如來与楞次定律相反,线圈中感应电流的磁场将吸引磁棒,使磁棒加速,动能增加.这增加的动能、磁场能和线圈中生的热都系无屮生冇,显然违反能最守恒定律.\n3分3分2分2分3分2分2分1分1分1分1分3分参考答案一选择题(共24分)DCBCCDDC二填空题(共24分)9(木题3分)10(本题3分)如4tiR11(本题4分)-“o'12(本题3分)42aIB13(本题4分)无感应电流无感应电流14(木题4分)Og段电动势方向由Q指向0.--BcolJ20_*eBd(2—d)15(本题3分)1:16参考解:吩貉霁畤“2二+“(才厂/兀(盃/4)必:W?=盃:盃=1:16三计算题(共47分)16(本题5分)解:将导线分成1、2、3、4四部份,各部分在0点产生的磁感强度设为耳、B?、也、B4.根据亞加原理0点的磁感强度为:B=B、+B°+B?+Bq・・・&、心均为0,故b=b2+B31分\nB3=-(sin0、-sin0〕)=伍""414也-4k/?=〃()//(2兀/?)方向®其中a=R/^2,sin0?=sin(兀/4)=^2/2sin0i=sin(-K/4)=-近/2・・・_如+如8/?2兀R17(本题12分)解:当只有一块无穷大平面存在时,D_1•B=2^=V^(y+-)方向®2分2/?4兀利用安培环路定理,町知板外的磁感强度值为4分现有两块无穷人平面,打与■夹角为&,因&丄,圧丄.,故百和圧夹角也为&或兀—0.⑴在两面Z间&和爲夹角为(兀一&)故2分2分2分2分Bj=*“0(年+岸一2也8$&)"2(2)在两面之外B[和鸟2的夹角为&,故◎+2;+2和;COS&)"(3)当I,=i2=i,&=0时,有Bj——a/2/ZqZV1—cos0—02B,=—V2/z()zV1+cos0=yj18(木题5分)解:应川安培坏路定理和磁场魯加原理可得磁场分布为,1=空+—吒—2tuc2兀(3a—x)B的方向垂直兀轴及图面向里.19(本题5分)解:长直导线AC和BQ受力大小相等,方向相反H.在同一直线上,故合力为零•现计算半圆部分受力,取电流元0,dF=ldlxB即dF=IRBdO2分由于对称性XdF<=0n・・・F=FX=jdFv=pRBsin&de=2R/B3分0方向沿y轴正向20(本题10分)\n解:两个载同向电流的长血导线在如图朋标x处所产牛的磁场为\n"念(丄+—L_)2kxx-r{+r2选顺时针方向为线框回路正方向,则妇阳警(了r\dx)x-rx+r2=丛In(也.匕)2兀rxr2£=dO=“0。比“+“皿+卩严/dr2k甘2dr=_如酬]n[©+历©+b)]cos勿2兀21(木题10分)解:动生电动势£肿=J(vxB)-dfMN为计算简单,可引入一条辅助线M/V,构成闭合回路MdVM,闭合回路总电动势£总=£MeN+£NM~°SeN=~£NM=目冲-v型肛二-如耳旦MNa-b2亦2兀a-b负号表示勺站的方向打X轴相反.u{Jnta+b、宀一In方向N-M2兀a-b血,泌In皿2兀a-bUm-UnMNMN1MNhn回答问题(共5分)22(本题5分)答:例如在磁棒靠近线圈时,线圈中产生感应电流,按楞次定律,线圈电流方向M如图所示,这样线圈阻碍磁棒靠近,使磁林的动能转化为线圈的磁场能和线圈中因有电流而牛:的热.2分如果与楞次定律相反,线圈屮感应电流的磁场将吸引磁棒,使磁棒加速,动能增加.这增加的动能、磁场能和线圈屮牛的热都系无中生有,显然违反能量守恒定律.3分