5统计学文献new

5统计学文献new

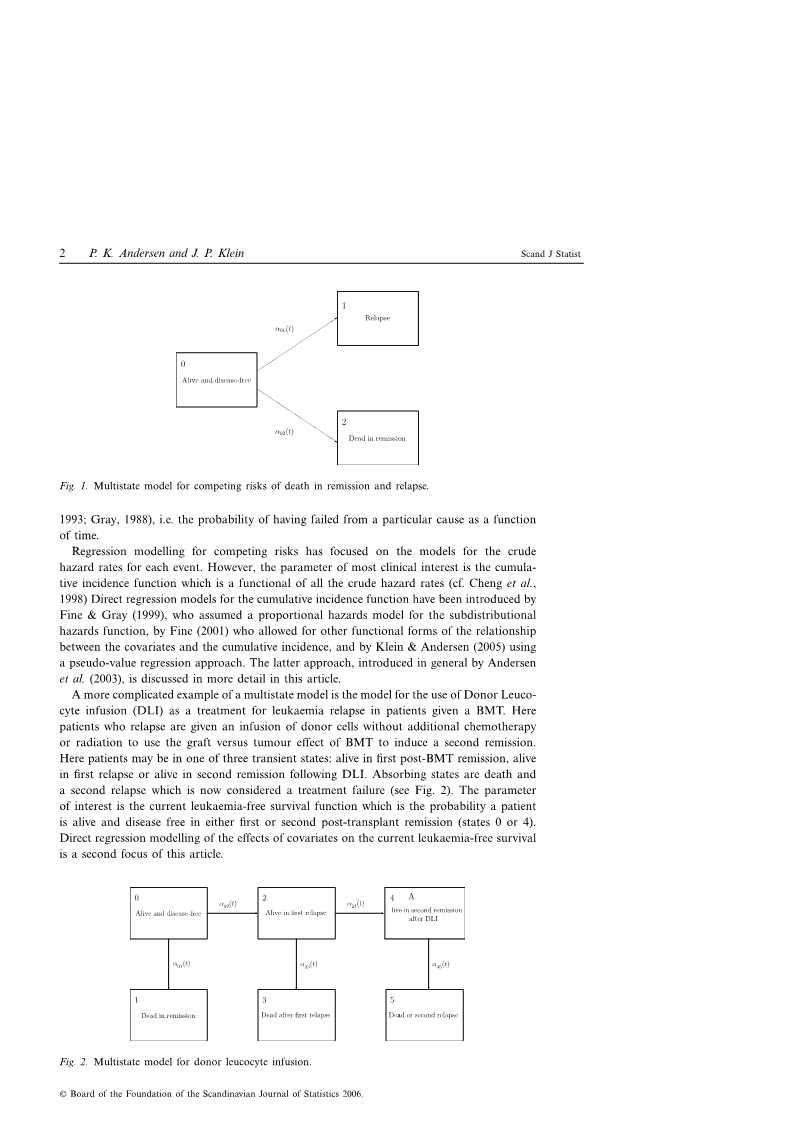
doi:10.1111/j.1467-9469.2006.00526.x©BoardoftheFoundationoftheScandinavianJournalofStatistics2006.PublishedbyBlackwellPublishingLtd,9600GarsingtonRoad,OxfordOX42DQ,UKand350MainStreet,Malden,MA02148,USA,2006RegressionAnalysisforMultistateModelsBasedonaPseudo-valueApproach,withApplicationstoBoneMarrowTransplantationStudiesPERK.ANDERSENDepartmentofBiostatistics,UniversityofCopenhagenJOHNP.KLEINDivisionofBiostatistics,MedicalCollegeofWisconsinABSTRACT.Typically,regressionanalysisformultistatemodelshasbeenbasedonregressionmodelsforthetransitionintensities.Thesemodelsleadtohighlynonlinearandverycomplexmodelsfortheeffectsofcovariatesonstateoccupationprobabilities.Wepresentatechniquethatmodelsthestateoccupationortransitionprobabilitiesinamultistatemodeldirectly.Themethodisbasedonthepseudo-valuesfromajackknifestatisticconstructedfromnon-parametricestimatorsfortheprobabilityinquestion.Thesepseudo-valuesareusedasoutcomevariablesinageneralizedestimatingequationtoobtainestimatesofmodelparameters.Weexaminethisapproachanditspropertiesindetailfortwospecialmultistatemodelprobabilities,thecumulativeincidencefunctionincompetingrisksandthecurrentleukaemia-freesurvivalusedinbonemarrowtransplants.Thelatteristheprobabilityapatientisaliveandineitherafirstorsecondpost-transplantremission.Thetechniquesareillustratedonadatasetofleukaemiapatientsgivenamarrowtransplant.Wealsodiscussextensionsofthemodelthatareofcurrentresearchinterest.Keywords:bonemarrowtransplantation,competingrisks,generalizedestimatingequations,multistatemodel,pseudo-observations,stateoccupationprobability,transitionprobability1.IntroductionMultistatemodelsariseinanumberofcontextsinbothengineeringandmedicalsciences.Inengineeringapplicationsmultistatemodellingoccursintheanalysisofcoherentsystems.Inmedicalapplications,themotivationforthisarticle,multistatemodelsariseinattemptingtounderstandcomplexdiseaseortreatmentprocesses.AsurveyofproblemsinmultistatemodelsisfoundinAndersen&Keiding(2002).Inmoststudiesofmultistatemodelsweareinterestedinhowcovariatesmayaffecttheprobabilityapatientwillbeinaparticularstateatagivenpointintime.Theseregressionmodelsarethefocusofthisarticle.Mostofthetypesofoutcomewetypicallyseewhenanalysingsurvivaldatacanbecon-sideredasamultistatemodel.Thesimplestcaseofasingleeventsuchasdeathcanbecon-sideredamultistatemodelwithonetransientstate,aliveandoneabsorbingstate,death.Theproblemofcompetingrisksisoneofthesimplestmultistatemodels(Andersenetal.,2002).Hereoccurrenceofoneofthecompetingriskeventsprecludestheobservationoftheotherrisks,seeFig.1.Agoodexampleofcompetingrisks,usedinlatersections,istherecoveryprocessofpatientsgivenahaematopoieticstemcelltransplant(oftenknownasabonemar-rowtransplant,BMT)forleukaemia.Herethecompetingrisksarerelapseoftheleukaemiaanddeathinremission,bothofwhichsignalthatthepatienthasfailedthetransplant.Mod-ellingofthecompetingrisksassumingahomogeneouspopulationhasfocusedonestimatingthecrude(orcause-specific)hazardrates(cf.Andersenetal.,1993;Crowder,2001;Kulathinal&Gasbarra,2002)orthecumulativeincidencefunction(cf.Pepe&Mori,1993;Pepeetal.,\n2P.K.AndersenandJ.P.KleinScandJStatistFig.1.Multistatemodelforcompetingrisksofdeathinremissionandrelapse.1993;Gray,1988),i.e.theprobabilityofhavingfailedfromaparticularcauseasafunctionoftime.Regressionmodellingforcompetingriskshasfocusedonthemodelsforthecrudehazardratesforeachevent.However,theparameterofmostclinicalinterestisthecumula-tiveincidencefunctionwhichisafunctionalofallthecrudehazardrates(cf.Chengetal.,1998)DirectregressionmodelsforthecumulativeincidencefunctionhavebeenintroducedbyFine&Gray(1999),whoassumedaproportionalhazardsmodelforthesubdistributionalhazardsfunction,byFine(2001)whoallowedforotherfunctionalformsoftherelationshipbetweenthecovariatesandthecumulativeincidence,andbyKlein&Andersen(2005)usingapseudo-valueregressionapproach.Thelatterapproach,introducedingeneralbyAndersenetal.(2003),isdiscussedinmoredetailinthisarticle.AmorecomplicatedexampleofamultistatemodelisthemodelfortheuseofDonorLeuco-cyteinfusion(DLI)asatreatmentforleukaemiarelapseinpatientsgivenaBMT.HerepatientswhorelapsearegivenaninfusionofdonorcellswithoutadditionalchemotherapyorradiationtousethegraftversustumoureffectofBMTtoinduceasecondremission.Herepatientsmaybeinoneofthreetransientstates:aliveinfirstpost-BMTremission,aliveinfirstrelapseoraliveinsecondremissionfollowingDLI.Absorbingstatesaredeathandasecondrelapsewhichisnowconsideredatreatmentfailure(seeFig.2).Theparameterofinterestisthecurrentleukaemia-freesurvivalfunctionwhichistheprobabilityapatientisaliveanddiseasefreeineitherfirstorsecondpost-transplantremission(states0or4).Directregressionmodellingoftheeffectsofcovariatesonthecurrentleukaemia-freesurvivalisasecondfocusofthisarticle.Fig.2.Multistatemodelfordonorleucocyteinfusion.©BoardoftheFoundationoftheScandinavianJournalofStatistics2006.\nScandJStatistRegressionanalysisofmultistatemodels3Inthenextsection,webrieflyreviewhowonemayobtainestimatesofstateprobabili-tiesformultistatemodels.Insection3,weshowhowtheseestimatorscanbeusedtoobtainpseudo-valuesandtherebyregressionmodelsforstateprobabilitiesusingageneralizedlinearmodel.Insection4,wefocusontheproblemofdirectregressionmodellingofthecumulativeincidencefunctionforcompetingrisksdata.Insection5weaddresstheproblemofregres-sionmodelsforthecurrentleukaemia-freesurvival.Finally,insection6,wediscusssomeextensionsofthepseudo-valueapproach.2.EstimationinmultistatemodelswithnocovariatesWeconsideramultistatemodelwithstatespace0,1,...,K.LetX(t)denotethestatethatanindividualisinattimet.WeareinterestedinestimationandmodellingofthetransitionprobabilitiesgivenbyPhj(s,t)=pr[X(t)=j|X(s)=h,Fs−],wherehandjarestatesandFs−isthehistoryofthemultistateprocessovertheinterval[0,s).Notethatingeneralthishistorymayincludeasetoffixedortime-dependentcovariatesaswellasthevaluesofX(u),u

查看更多