社会统计学复习整理

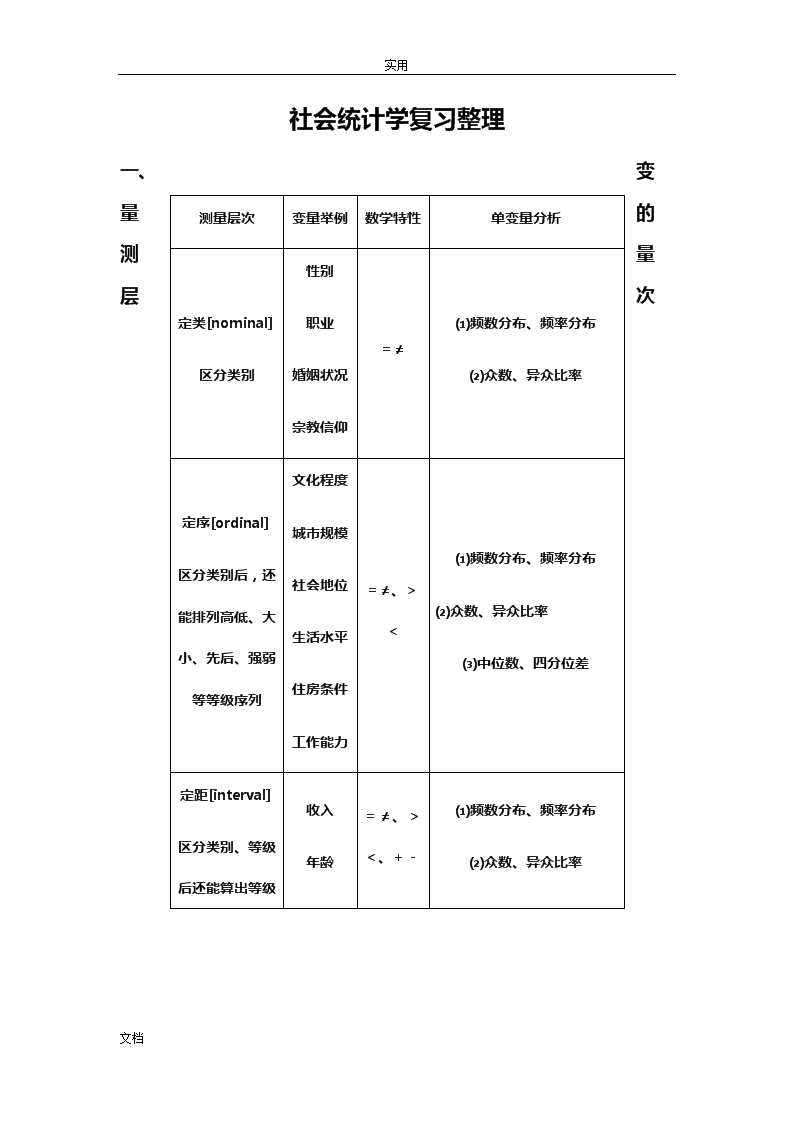
社会统计学复习整理

实用社会统计学复习整理一、变量的测量层次测量层次变量举例数学特性单变量分析定类[nominal]区分类别性别职业婚姻状况宗教信仰＝≠⑴频数分布、频率分布⑵众数、异众比率定序[ordinal]区分类别后，还能排列高低、大小、先后、强弱等等级序列文化程度城市规模社会地位生活水平住房条件工作能力＝≠、＞＜⑴频数分布、频率分布⑵众数、异众比率⑶中位数、四分位差定距[interval]收入年龄＝≠、＞＜、＋－⑴频数分布、频率分布⑵众数、异众比率文档\n实用区分类别、等级后还能算出等级间的差距数量，但没有实际意义的“0”时间出生率性别比⑶中位数、四分位差⑷平均数、标准差、离散系数定比[ratio]区分类别、等级后还能算出等级间的差距数量，但具有实际意义的“0”收入年龄时间出生率性别比＝≠、＞＜、＋－、×÷⑴频数分布、频率分布⑵众数、异众比率⑶中位数、四分位差⑷平均数、标准差、离散系数文档\n实用二、判断变量层次的技巧1.首先所有的变量都是定类变量。2.其次看变量的取值能否比较大小，不能这个变量只能是定类变量。3.最后如果这个变量能够比较大小，那么就看变量取值加减乘除是否有意义，如果有意义就是定距变量，如果没有意义就只能是定序变量。三、变量层次的比较定类变量、定序变量和定比变量的数层次是从低到高排列的，高层次的变量同时具有低层次变量的功能。四、相关分析方法变量层次相关系数是否对称取值范围PRE意义检验定类-定类定类-定序λ不对称【0，1】有X²文档\n实用定序-定序G否【-1，1】有Z定类-定距定序-定距Eta²不对称【0，1】无F定距-定距r对称【-1，1】无Fr²对称【0，1】有第二节简化一个变项的分布一、定类变量1.统计表：用表格的形式来表示变量频次（或频率）分布的一种工具。2.统计表必备的内容：（1）表号、标题（2）标识行：变量名、对应数据说明（频次、频率）（3）主题行：变量取值的统计数据（4）表尾：如果是引用必须说明资料来源二、定序变量1.适合定序变量的简化资料的方法（1）累加次数：把次数逐渐相加起来，分为向上累加次数（cf↑）和向下累加次数(cf↓)。文档\n实用（1）累加频率：把各级的百分率逐渐相加。也分为向下累加百分率和向下累加百分率。2.cf↑的计算方法就是按照变量取值的等级从低往高逐层相加。3.cf↓计算方法就是按照变量取值的等级从高往低逐层相加。Øcf↑表示低于某个等级的频数有多少Øcf↓表示高于某个等级的频数有多少一、定距变量1.定距变量的简化工具是：分组、直方图和折线图。2.连续型定距变量的分组统计（1）组数：分组的数量，一般5到7组合适，分为等距分组和非等距分组。（2）组限：包括上限（up）和下限（low）（3）标识下限和标识上限，例500—699（4）真实下限：标识下限—0.5；真实上限：标识上限+0.5.（5）组距：真实上限与真实下限之差。（6）组中值：真实上限与真实下限的平均值。第三节集中趋势测量法1.文档\n实用集中趋势：用一个典型的变量值或特征值来代表全体变量的问题，用这个数值来代表变项的资料分布，以反映资料的集结情况。1.集中趋势测量的意义就是可以根据这个代表值来估计或预测每个研究对象的数值。一、定类变量1.众值（Mode）Mo：用具有频数最多的变量的取值来表示变量的集中值。2.众值的特征：（1）：众值理论上可以用于定类、定序和定距三个层次的变量来描述集中趋势，但是由于众指不精确，一般只用于定类层次的变量。（2）：众值最好找，是最容易求出的值，但它精确度也是最差的。二、定序变量1.中位值（Md）。2.分组数据求中位值公式：Md=L+(n/2-cf↑/n)(U-L)L：中位值的真实下界值U：中位值的真实上界值n：中位值组的频数cf↑：低于中位值所在组的累加（向上）频次文档\n实用N：调查总数Md位值：N/2一、定距变量1.均值（Mean）:将变量的各个数值相加起来，除以总个数，求取一个平均值的数值，一般用¯x来表示。2.均值的特征：l仅适合定距层次的变量l它最灵敏，预测的精确度最高l对资料所提供的信息运用得最充分3.均值的求法（一）原始数据求均值：X=∑X1/N(X表示变量x的均值；∑X1表示变量观察值的总和。)（二）根据频次分布求均值：¯x=∑n1X1∑n2(¯x表示变量X的均值；∑n1X1表示变量的每一个取值和该变量频数相乘的和；∑n2表示把变量的每个取值下的频次都加起来，即调查总数N)文档\n实用(三)分组数据求均值：¯x=∑n1b1∑n1(n1表示每组次数，b表示每组的组中值，∑n1表示个案数目)第四节离散趋势测量法l离散趋势测量法：是求出一个值来表示个案与个案之间的差异情况。l离散趋势或离散特征可以告诉我们估计值误差的大小。一、定类变量（异众比率V）V就是非众值的次数与全部个案数目的比率。V=N-fmoN(N-全部个案数目；fmo-众值的次数)V值越小，众值代表性越好。二、定序变量1.极差(R)—观察的最大值与最小值之差。2.四分互差：将数值排序，分为四个等分，第一个四分位置的值与第三个四分位置的值的差异。四分位差Q=Q75-Q25文档\n实用(一)未分组数据:2234691010111315Md的位置=N+1/2=11+1/2=6Q25的位置=N+1/4=11+1/4=3（第三位数）Q75的位置=34（N+1）=34（11+1）=9（第九位数）所以，四分位差Q=Q75-Q25=11-3=8(二)分组数据1.中位值公式=Md=L+(N2-cf↑)/n(U-L)2.Q25=L+(N4-cf↑)/n(U-L)L：四分之一位值组的真实下界值U：四分之一位值组的真实上界值n：四分之一位值组的频数cf↑：低于四分之一位值组的向上累加频次N：调查总数Q25位置=N/4;3.Q75=L+(3N4-cf↑)/n(U-L)L：四分之三位值组的真实下界值U：四分之三位值组的真实上界值n：四分之三位值组的频数文档\n实用cf↑：低于四分之三位值组的向上累加频次N：调查总数Q75位置=3N/4;一、定距变量(一)标准差σ与方差σ²σ=1NN∑Xi2-(∑Xi)²(δ即对均值的偏差平方均值的平方根)σ²=（Xi-x)²N(二)根据未分组的频次分布求方差σ=1NN∑niXi2-(∑niXi)²N-调查总数；Xi-表示变量的每个取值；ni-表示每个取值的频次(三)分组数据求方差——用组中值代替bi代替xi代入公式中σ=1NN∑nibi2-(∑nibi)²第三章概率一、概率文档\n实用1.不可能事件的概率：P(O)=02.必然事件的概率：P(S)=13.随机事件的概率：0≦P(E)≦1二、两个重要概念1.普查：对统计总体的全部单位进行调查以搜集资料统计资料的工作。2.抽查：按照某种方法以总体中抽取一部分样本进行调查，以搜集统计资料的工作。三、频率分布于概率分布的关系1.频率分布是实验值，是可以变化的，称之为统计分布或经验分布。2.概率分布是理论值，是唯一的，称之为理论分布。3.当观测次数很大时，随机变量取值的频率接近于其概率，这时随机变量的统计分布与理论分布将大致相符。四、总体均值和方差1.总体均值（E）:随机变量各取值分别乘取值的概率的总和。E(ξ)=µ=∑PiXi2.总体方差（D）:就是随机变量偏离总体均值的程度。文档\n实用D=S²=E(X²)-［E(x)］²3.总体均值和样本均值的区别：l总体均值是对研究对象进行普查后得出的均值。l样本均值是对从总体中抽取的样本数据计算出来的均值。4.总体方差与样本方差的区别：l总体方差是对研究对象进行普查后，利用数据算出来的方差。l样本方差是根据从总体中抽取出的样本的调查总数据，计算出来的方差。5.总体均值方差和样本均值方差表示法1.总体均值E=µ，总体方差D=σ²，总体标准差=σ2.样本均值=¯x，样本方差=s²，样本标准差=S6.结论1.通过普查，可以得出概率、总体均值E(µ)、总体方差D(σ²)，这些值我们称为参数值。2.通过抽查，可以得出频率、样本均值¯x、样本方差s²，这些值我们称为统计值。3.当样本为大样本(N≧30)，频率≈概率、样本均值≈总体均值、样本方差≈总体方差。文档\n实用4.当样本数无穷接近总体数的时候，频率=概率、样本均值=总体均值、样本方差=总体方差。5.统计学的任务就是如何利用统计值来推论参数值（统计推论），实现我们的研究目的。第四章常见统计分布第一节二点分布一、二点分布（0-1分布）:就是变量的取值只有两类的分布。如：性别。二、二分变量的分布律：随机变量如果满足二点分布，则其概率分布为——P(ξ=0)=q；P(ξ=1)=P；P+q=1ξ01P=(ξ=Xi)qP第二节二项分布一、二项分布：在相同条件下进行n次独立试验，每次试验只有两种可能的结果，事件A出现的概率P(A)=P,事件A不出现的概率P(A)=1-p=q.文档\n实用第三节正态分布一、什么是正态分布？中心极限定理：对于任何变量，不管其原有分布如何，如果把它们n个加在一起，当n大于一定数之后（n>30）,那么其和的分布必然接近正态分布。二、正态分布密度曲线的特点1.一个高峰2.一个对称轴——X=µ3.一个渐近线——X轴4.正态分布曲线是单峰值对称的，因此这种分布的变量，其众值、中位值和均值是重叠的。5.正态分布下的面积为1.三、正态曲线的参数意义1.正态分布的两个参数是µ（总体均值）和σ（总体方差）。2.两个参数对曲线形状的影响：(1)φ（X）在x=μ处达到峰值，以直线x=μ为对称轴。在σ一定的情况下，若μ增大，图形右移；若μ减小，则左移，但形状不变。(2)当μ值一定时，σ值越小，则对应的图形越尖越瘦。文档\n实用第四节标准正态分布标准正态分布：标准正态分布就是通过公式把一般正态分布转化而来，这样把不同的正态分布都统一为（0，1）的正态分布，然后再通过查表求出两点之间的概率。公式：Ζ=X-μσ1.标准正态分布的μ=0，σ=1，其图形以Ζ=0为对称轴。2.标准正态分布记作X～N(0，1),一般正态分布记作X～N（μ～σ²）3.标准正态分布的图形唯一的，其值可以通过查表（附表4）求得。（只有标准正态分布才能查表，如果是一般正态分布则先用公式转化为标准正态分布）4.正态分布N(μ～σ²)和标准正态分布N(0，1)面积之间的对应关系：当X=μ+σ时，Ζ=X-μσ=1当X=μ-σ时，Ζ=X-μσ=-1第五节常用统计分布文档\n实用一、X²分布（卡方分布）设变量ξ1、ξ2，、、、、、、ξk相互独立，且都服从N(0，1)，则X²=（ξ1）²+(ξ2)²+…+(ξk)²称为自由度为K的X²分布。记作：ξ～X²（k）二、t分布设随机变量ξ和η独立，且ξ～N(0，1)，η～X²（k）,则随机变量t(t=ξηk)服从自由度为k的t分布，记作t～t(k)。三、F分布设随机变量ξ和η独立，且ξ～X²（k1）η～X²（k2）,则随机变量F(F=ξk1ηk2)服从自由度（k1，k2）的分布记作F～F（k1，k2）。第五章参数估计一、关于抽样的一些概念1.总体：构成总体的所有元素的集合，元素则是构成总体的最基本的单位。2.样本：从总体中按一定方式抽取出来的一部分元素的集合。文档\n实用3.抽样：从总体中，按一定的方式选择或抽取样本的过程。4.抽样单位：一次直接抽样所使用的基本单位。二、统计推论1.统计推论：根据局部资料（样本资料）对总体进行推断的过程。2.样本资料的特点：（1）样本资料来源于总体，因此局部资料的特性在某种程度上能反映总体的特征。（2）由于抽样的随机性，则抽样的结果有可能不等于总体的结果。（3）当样本达到一定规模的时候(大样本)，呈现规律性。3.统计值：从样本中计算出来的数值。4.参数值：总体的数值。5.统计推论的内容分为两个部分：（1）通过样本的统计值对总体的未知参数进行估计，称为参数估计。（2）通过样本对总体的某种假设进行检验，称为假设检验。三、抽样分布1.样本均值文档\n实用的分布：我们按照简单随机抽样的方法，从总体中抽取样本，因为每一个个体被抽中的机会具有随机性，所以每一次抽出的样本其均值都不同，那么在同一个总体中，抽取n次就有n个样本均值（），而样本均值的分布就是这n个样本均值的分布。2.样本方差S2的分布：就是n个样本方差的分布。第三节参数的点估计点估计：直接用样本计算出来的统计值来估计总体的参数值，由于它只是一个点值，所以称参数的点估计。一、总体参数的点估计公式1.总体均值μ的点估计值为样本均值XX=1ni=0nXi2.总体方差σ2的点估计值为样本方差S2文档\n实用S2=1n-13.总体标准差σ的点估计值为样本标准差S第五节正态总体的区间估计一、区间估计：通过样本计算出一个范围来对总体未知参数进行估计。二、区间估计的概率表达式：nQ——未知参数（总体值）；n＾Q——统计值（样本值）；n【＾Q-ε，＾Q+ε】置信区间为Q的可能取值范围）；n1-a——置信度（置信区间包含Q可靠性程度）；一般是根据研究者想让自己的研究达到什么样的精确度而自己给定的。na——显著性水平（significant），表示用置信区间估计不可靠的概率。第六节大样本区间估计（一）σ2已知时，样本均值呈正态分布文档\n实用整理后得出μ的区间估计概率公式：所以，μ的双侧置信区间为：（二）大样本，总体分布满足x～N(μ,σ2)，但σ2未知时对μ进行区间估计：Z=ˉx-µssn(用样本标准差s代替总体标准差σ)整理后得出μ的区间估计概率公式：所以，μ的双侧置信区间为：•故总体成数P的区间估计公式为文档\n实用如果P未知，可以用＾P取代。（三）常用置信度下的置信区间当1-a=0.95时，置信区间为：1-a=0.99时，置信区间为：第六章假设检验的基本概念文档\n实用一、统计假设：依靠抽样数据对总体分布进行验证的假设，包括原假设和备择假设。二、原假设和备择假设1.原假设H0:又称之为虚无假设，根据已有的资料，或周密考虑后确定的，如果没有充分根据，是不会被轻易否定的。2.备选假设H1:又称研究假设，经过抽样调查，有充分根据否定原假设H0时，产生的假设。三、假设检验的基本原理大数定理：1.对事件进行大量观察时，事件的发生是有规律的，这种有规律性的数量成为概率。2.在大量观察中，频繁出现的事件具有较大的概率，反之，则具有小的概率。小概率原理：Ø认为小概率事件在一次观察中是不可能出现的,称为小概率原理。Ø如果在一次观察中出现了小概率事件，就否定原有事件具有小概率事件的假设。一、假设检验的思想1.文档\n实用经过抽样调查获得数据后，如果根据样本计算的某个统计量表明在原假设H0成立的条件下几乎是不可能发生的，我们就拒绝原假设，而接受备选假设。2.如果在原假设成立的条件下，根据样本所计算的某个统计量，发生的可能性很大的话，我们就接受原假设。五、相关名词：1.统计检验中的假定（前提）:是进行检验的前提或要求。如计算时，要求时正态分布，样本的抽取应该是随机抽样。2.统计量:用来检验总体的样本的函数f（x1，x2，…xn），常用的统计量有服从Z分布、t分布、F分布、X2分布等，他们的统计量分别对应为Z、t、F、X2。3.显著性水平(significance)α=小概率小概率的标准，小概率的数量界限。常用的显著性水平有α=0.10、0.05或0.01。4.临界值、接受域和拒绝域根据原假设作出统计量的分布图六、假设检验的两类错误1.弃真的错误——是在拒绝原假设时出现的错误，即将正确的原假设当作假的所犯的错误。弃真错误的大小就是a2.纳伪的错误——文档\n实用是接受原假设时出现的错误，即接受了实际上错误的原假设的错误。称为第二类错误。七、两类错误的关系——弃真错误减少导致纳伪错误的增大反之亦然。即，当显著性水平α减小时，由于拒绝域的减小，弃真的错误会减小，但由此而来的是接受域增大了，因而纳伪的概率增大，反之亦然。八、解决的方法－－增加样本容量。九、假设检验的四个步骤：1.成立原假设2.成立备择假设3.统计量4.拒绝域和接受域第九章列联表一、什么是列联表（一）相关：是指一个变项的值与另一个变项的值有连带性。即如果一个变项的值发生变化，另一个变项的值也有变化。（1）正相关（正比）：是指一个变项的值增加时，另一个变项的值也增加。（2）负相关（反比）：是指一个变项的值增加时，另一个变项的值却减少。文档\n实用（二）自变量、因变量：科学研究中，我们成立假设，一般假定某变项是因，另一变项是果，那么前者称之为自变量，后者称为因变量。（1）不对称关系：自变量影响因变量，因变量不影响自变量（2）对称关系：自变量和因变量互相影响。（三）列联表（交互分类表）：按照两个变量进行交互分类的频次分布表，其综合了两个变项的共同分布。即：我们先将数据按自变量x分类，然后分别统计自变量的每一取值下的因变量y的取值，然后形成的统计表。二、列联表要注意的问题1.线条要尽量的少，舍去不必要的线条。2.每个表的顶端要有表号和标题。3.表的顶端为自变量，表的左旁边为因变量。4.表的大小＝表的横行数目（rows，简写为r）×表的纵行数目（columns，简写为c）。5.表的下端和表的右边称为边缘分布。6.联合次数分布表和联合频率分布表可以互换。7.联合频率分布表中，一定要注明样本总数。8.应以自变量的方向计算百分比的方向。文档\n实用三、边缘分布1.边缘分布：只研究联合分布中某一变量的分布，而不管另一个变量的取值。2.关于y的边缘分布（N*j）：把联合分布中的概率，次数按行的方向加总起来的分布。3.关于x的边缘分布（Ni*）：把联合分布中的概率，次数按列的方向加总起来的分布。四、条件分布将其中一个变量控制起来取固定值，研究另一变量的分布，即得到第二个变量的条件分布。关于y的条件分布（控制x的取值），最多有c个。关于x的条件分布（控制y的取值），最多有r个。一、列联表中变量的相互独立性（自变量与因变量无关时）列联表中变量相互独立性时，则如下等式成立：NijNi*=N*jNx1x2N*j文档\n实用y1N11N21y2N12N22Ni*NPij=Pi*P*jx1X2P*jy1P11P21y2P12p22Pi*1六、列联表的检验1.检验的内容：x与y是否有关总体参数：pN（总体概率及总数）样本参数：＾Pn（样本频率及频次）2.列联表检验的原假设文档\n实用H0：Pij=pi*p*ji=1，2，…，cNijNi*=N*jNj=1，2，…，r七、列联表检验的统计量1.期望格值Eij是假定H0成立的条件下，每格内期望发生的频次（理论值）；2.样本格值nij是样本实测频次或观察频次。3.原假设成立的情况下，有下面的的等式：Eij≈ni*n*jN八、统计量X2九、列联强度文档\n实用1.r×c列联表——PRE测量法E1：不知道y与x的关系时，预测y的全部误差E2：知道y与x的关系后，用x去预测y的全部误差E1-E2：知道y与x的关系后预测y所减少的误差vPRE（Proportionalreductioninerror）称为减少误差比例，表示用x解释y时可以减少的误差的百分比。2.PRE的取值范围：PRE=0E1=E2则x与y无关PRE=1E2=0x与y完全相关0＜PRE＜1x与y部分相关e.g.PRE=0.8，说明用x预测y可以减少80%的误差，x与y高度相关3.Lamda系数（l）文档\n实用4.l系数取值范围:l=0x与y无关l=1x与y全相关0＜l＜1x与y部分相关,值越大表示x与y相关程度越高。5.T系数讨论1.非对称性。要求两个定类变项中有一个是自变项(x)另一是因变项(y)2.0≤τ≤1(τ=0无关;τ=1完全相关)3.具有PRE意义第十章等级相关一、名词文档\n实用1.同序对：设填问卷的A和B两个人，在变量X和Y(问卷上的两个问题，一为自变量，一为因变量)的等级分别为：(Xi,Yi)；（Xj,Yj）如果Xi>Xj,Yi>Yj,就称A和B是同序对。2.异序对：设填问卷的A和B两个人，在变量X和Y(问卷上的两个问题，一为自变量，一为因变量)的等级分别为：(Xi,Yi)；（Xj,Yj）如果Xi>Xj,Yind，G>0—两变量正相关；nd=0，G=1--两变量完全相关；lnsFα(1,n-2)文档