生物统计学考卷A卷

生物统计学考卷A卷

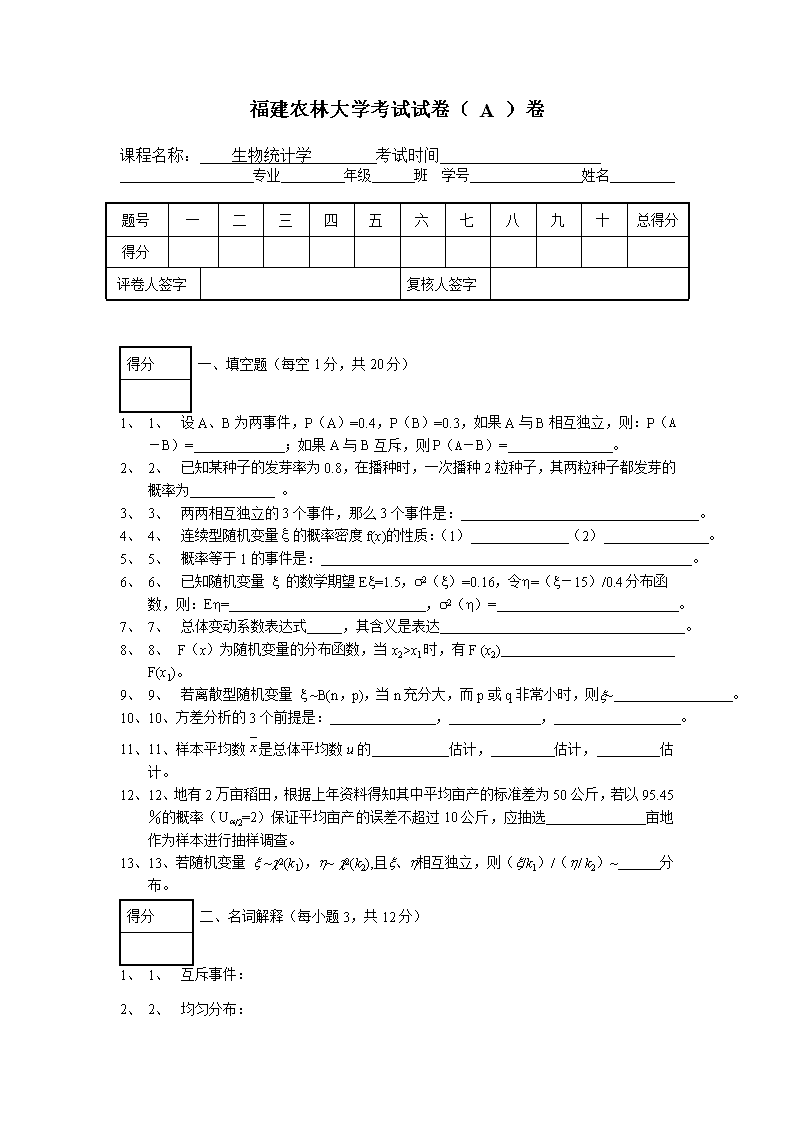
福建农林大学考试试卷（A）卷课程名称：生物统计学考试时间专业年级班学号姓名题号一二三四五六七八九十总得分得分           评卷人签字 复核人签字  得分一、填空题（每空1分，共20分）  1、1、   设A、B为两事件，P（A）=0.4，P（B）=0.3，如果A与B相互独立，则：P（A－B）=；如果A与B互斥，则P（A－B）=。2、2、   已知某种子的发芽率为0.8，在播种时，一次播种2粒种子，其两粒种子都发芽的概率为。3、3、   两两相互独立的3个事件，那么3个事件是：。4、4、   连续型随机变量ξ的概率密度f(x)的性质：（1）（2）。5、5、   概率等于1的事件是：。6、6、   已知随机变量x的数学期望Ex=1.5，s2（x）=0.16，令h=（x－15）/0.4分布函数，则：Eh=，s2（h）=。7、7、   总体变动系数表达式，其含义是表达。8、8、   F（x）为随机变量的分布函数，当x2>x1时，有F(x2)F(x1)。9、9、   若离散型随机变量x~B(n，p)，当n充分大，而p或q非常小时，则x~。10、10、方差分析的3个前提是：，，。11、11、样本平均数是总体平均数u的估计，估计，估计。12、12、地有2万亩稻田，根据上年资料得知其中平均亩产的标准差为50公斤，若以95.45％的概率（Ua/2=2）保证平均亩产的误差不超过10公斤，应抽选亩地作为样本进行抽样调查。13、13、若随机变量x~c2(k1)，h~c2(k2),且x、h相互独立，则（x/k1）/（h/k2）~分布。得分二、名词解释（每小题3，共12分）  1、1、   互斥事件： 2、2、   均匀分布：\n   1、3、    偏度： 2、4、   小概率原理：  得分三、问答题（每小题6分，共18分）  1、1、  假设A与B为互斥事件，且P（A）>0，P（B）>0，试证事件A与B不相互独立。    2、2、  在假设检验时，可能犯的两类错误是什么？请指出它们之间关系，如何克服它们之间矛盾。  3、3、  进行方差分析时，如果因素对实验结果有影响，而发现F检验却断定不了，这是为什么？请简单提出解决方法。     得分四、计算题（每小题10分，共50分）  1、设各试验相互独立，第i次试验得成功率为pi，求n次试验中成功次数得期望与方差。      2、设航空照片上某一点拍摄为有林地的概率为0.70，拍摄为无林地的概率为0.30，但某读员进行判断读时，如拍摄为有林地则被判读为有林地的概率为0.90，被判读为无林地概率为0.10，如拍摄为无林地则被判读为有林地的概率为0.20，被判读为无林地的概率为0.80，试求该点被判读为有林地的概率。对于航测照片上所拍摄之一点判读为有林地，该点确系有林地的概率。   \n        3、某林区面积很大，预备调查结果，每0.1hm2林地上蓄积量的平均值为8.64m3，标准差为5.32m3，如果采用重复随机抽样方法，以95%的可靠性，去估计每0.1hm2林地上的平均蓄积量，并要求精度在85%以上，问至少应抽取多少块0.1hm2的林地组成样本。         4、柳杉的正常叶色（绿）是显性基因A控制，异常叶色a是隐性基因控制，观测正常与异常杂交的第二代苗木120株中，正常的95株，不正常的25株，问柳杉叶色分离是否符合分离规律，即3:1的比例分离（a=0.05，c20.05（1）=3.841）          5、在某林分内随机抽取6块样地，测定了样地每公顷胸高断面积xi与每公顷蓄积量yi，得到表中的数据，根据专业知识已知胸高断面积与蓄积量成线性关系，试求出回归方程，计算样本相关系数并作显著性检验。F0.05（1，4）=7.71样地号123456断面积xi（m2/ha）24.326.528.730.531.732.9蓄积量yi（m2/ha）314376436498557612 福建农林大学考试试卷答案要点（A）卷课程名称：生物统计学考试时间专业年级班学号姓名\n题号一二三四五六七八九十总得分得分           评卷人签字 复核人签字  得分一、填空题（每空1分，共20分）  1、1、   设A、B为两事件，P（A）=0.4，P（B）=0.3，如果A与B相互独立，则：P（A－B）=0.28；如果A与B互斥，则P（A－B）=0.4。2、2、   已知某种子的发芽率为0.8，在播种时，一次播种2粒种子，其两粒种子都发芽的概率为0.64。3、3、   两两相互独立的3个事件，那么3个事件是：不一定独立4、4、   连续型随机变量ξ的概率密度f(x)的性质：（1）f（x）>0（2）。5、5、   概率等于1的事件是：可能是必然事件也可能是随机事件。6、6、   已知随机变量x的数学期望Ex=1.5，s2（x）=0.16，令h=（x－15）/0.4分布函数，则：Eh=0，s2（h）=1。7、7、   总体变动系数表达式s/m，其含义是表达总体在某个标志上相对变动程度。8、8、   F（x）为随机变量的分布函数，当x2>x1时，有F(x2)≥F(x1)。9、9、   若离散型随机变量x~B(n，p)，当n充分大，而p或q非常小时，则x~泊松分布。10、10、方差分析的3个前提是：正态，独立，等方差。11、11、样本平均数是总体平均数u的无偏估计，有效估计，一致估计。12、12、地有2万亩稻田，根据上年资料得知其中平均亩产的标准差为50公斤，若以95.45％的概率（Ua/2=2）保证平均亩产的误差不超过10公斤，应抽选100亩地作为样本进行抽样调查。13、13、若随机变量x~c2(k1)，h~c2(k2),且x、h相互独立，则（x/k1）/（h/k2）~F分布。得分二、名词解释（每小题3，共12分）  1、1、   互斥事件：如果在试验结果中，事件A与事件B不可能同时出现，亦即P（AB）=P（f）=02、2、   均匀分布：具有概率密度函数为\n，由这一概率密度所表示的概率分布律称为均匀分布，写作x∽U（a，b）。1、3、    偏度：是表明随机变量x分布偏斜方向和偏斜程度的特征数。2、4、   小概率原理：概率很小的事件在一次试验中几乎是不会发生的。得分三、问答题（每小题6分，共18分）  1、1、   假设A与B为互斥事件，且P（A）>0，P（B）>0，试证事件A与B不相互独立。答案要点：假设A与B相互独立，导致P（AB）=P（A）×P（B），由于A与B为互斥事件，所以P（AB）=0，即P（A）×P（B）=0，与P（A）>0，P（B）>0相矛盾。2、2、   在假设检验时，可能犯的两类错误是什么？请指出它们之间关系，如何克服它们之间矛盾。答案要点：即弃真错误、采伪错误，两者变化互相矛盾3、3、   进行方差分析时，如果因素对实验结果有影响，而发现F检验却断定不了，这是为什么？请简单提出解决方法。答案要点：当fe（误差项自由度）很小时，F检验的灵敏度是低的，即因素明明有显著影响但F检验却断定不了。当fe越大，F检验灵敏度越高，但欲使fe大就要求试验的项数增多，这是一个矛盾，一般在有条件的情况下希望保证fe在12。如实在有困难作F检验时，将a放宽至0.20并注意在进一步的实践中来检验所作的结论。得分四、计算题（每小题10分，共50分）  1、设各试验相互独立，第i次试验得成功率为pi，求n次试验中成功次数得期望与方差。答案要点：设xi为第i次试验成功得随机变量（i=1，2，…，n），则xi=x10p（xi=x）pi1－piExi=pi；Exi2=pi；s2（xi）=Exi2－（Exi）2=pi－pi2=pi（1－pi）；ESxi=SExi=Spi；s2（Sxi）=Ss2（xi）=Spi（1－pi）2、设航空照片上某一点拍摄为有林地的概率为0.70，拍摄为无林地的概率为0.30，但某读员进行判断读时，如拍摄为有林地则被判读为有林地的概率为0.90，被判读为无林地概率为0.10，如拍摄为无林地则被判读为有林地的概率为0.20，被判读为无林地的概率为0.80，试求该点被判读为有林地的概率。对于航测照片上所拍摄之一点判读为有林地，该点确系有林地的概率。答案要点：设A=被判读为有林地；B1=拍摄为有林地；B2=拍摄为无林地。显然，B1、B2为互斥事件的完备群，P(B1)=0.70，P(B2)=0.30，，因此，由全概率公式可求出：，且P(A)>0由前知，由逆概率公式计算出：3、某林区面积很大，预备调查结果，每0.1hm2林地上蓄积量的平均值为8.64m3，标准差为5.32m3，如果采用重复随机抽样方法，以95%的可靠性，去估计每0.1hm2林地上的平均蓄积量，并要求精度在85%以上，问至少应抽取多少块0.1hm2的林地组成样本。\n答案要点：采用大样本U估计方法。，s=5.32m3，Þ。则至少应取66块0.1hm2的林地组成样本。4、柳杉的正常叶色（绿）是显性基因A控制，异常叶色a是隐性基因控制，观测正常与异常杂交的第二代苗木120株中，正常的95株，不正常的25株，问柳杉叶色分离是否符合分离规律，即3:1的比例分离（a=0.05，c20.05（1）=3.841）答案要点：（1）假设H0：分离比例符合3:1（2）从H0为真出发，算出理论频数分别为：np1=120×3/4=90，np2=120×1/4=30（3）计算：（4）对于检验水平a=0.05，自由度f=2-1=1，c2a=3.841；而c2=1.111

查看更多