- 2022-08-13 发布 |
- 37.5 KB |
- 10页

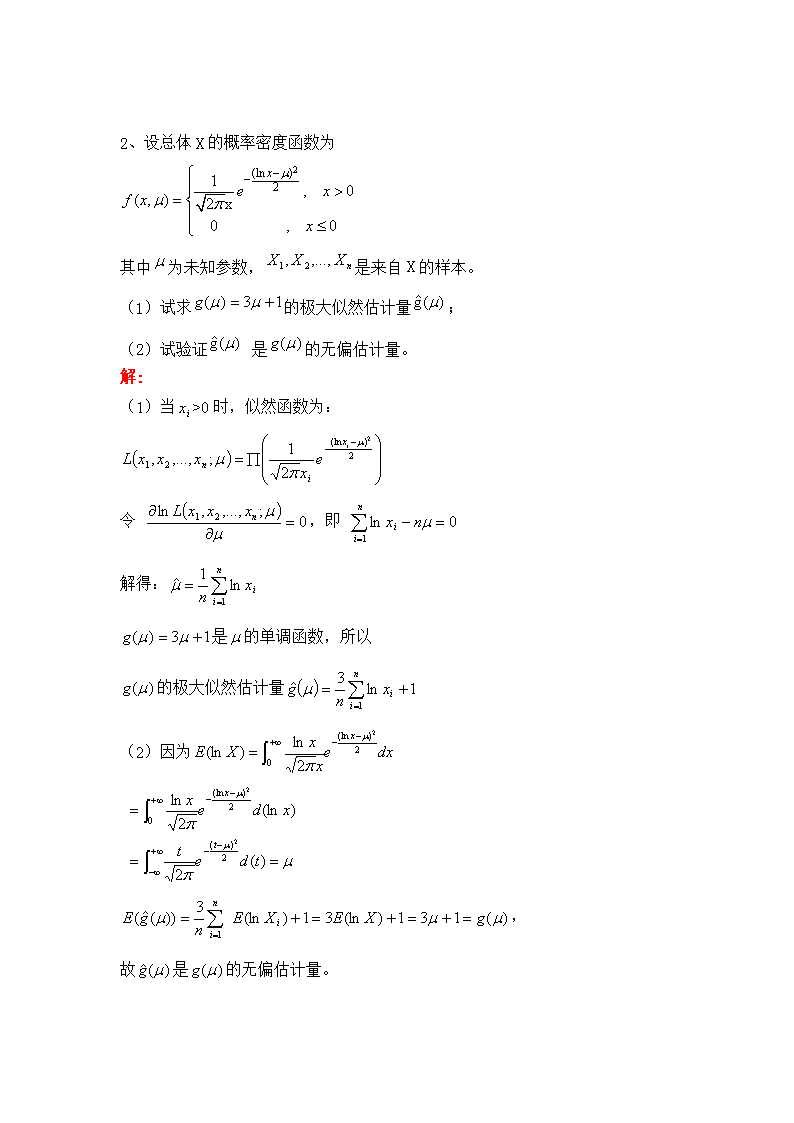

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
[应用统计学]解答
应用统计学请在以下五组题目中任选一组作答,满分100分。第一组:一、计算题(每小题25分,共50分)1、下表中的数据是主修信息系统专业并获得企业管理学士学位的学生,毕业后的月薪(用y表示)和他在校学习时的总评分(用x表示)的回归方程。总评分月薪/美元总评分月薪/美元2.628003.230003.431003.534003.635002.93100解:2.628006.76728078400003.4310011.561054096100003.6350012.9612600122500003.2300010.24960090000003.5340012.2511900115600002.931008.4189909610000=19.2=18900=62.18=6091059870000设==581.08=18900/6-581.08*19.2/6=1290.54于是\n2、设总体X的概率密度函数为其中为未知参数,是来自X的样本。(1)试求的极大似然估计量;(2)试验证是的无偏估计量。解:(1)当>0时,似然函数为:令,即解得:是的单调函数,所以的极大似然估计量(2)因为,故是的无偏估计量。\n二、简答题(每小题25分,共50分)1.在统计假设检验中,如果轻易拒绝了原假设会造成严重后果时,应取显著性水平较大还是较小,为什么?答:取显著性水平较小,因为如果轻易拒绝了原假设会造成严重后果,那就说明在统计假设检验中,拒绝原假设的概率要小,而假设检验中拒绝原假设的概率正是事先选定的显著性水平α。2.加权算术平均数受哪几个因素的影响?若报告期与基期相比各组平均数没变,则总平均数的变动情况可能会怎样?请说明原因。答:加权算术平均数受各组平均数和次数结构(权数)两因素的影响。若报告期与基期相比各组平均数没变,则 总平均数的变动受次数结构(权数)变动的影响,可能不变、上升、下降。如果各组次数结构不变,则总平均数不变;如果组平均数高的组次数比例上升,组平均数低的组次数比例下降,则总平均数上升;如果组平均数低的组次数比例上升,组平均数高的组次数比例下降,则总平均数下降。第二组:一、计算题(每小题25分,共50分)1、某一汽车装配操作线完成时间的计划均值为2.2分钟。由于完成时间既受上一道装配操作线的影响,又影响到下一道装配操作线的生产,所以保持2.2分钟的标准是很重要的。一个随机样本由45项组成,其完成时间的样本均值为2.39分钟,样本标准差为0.20分钟。在0.05的显著性水平下检验操作线是否达到了2.2分钟的标准。答案:根据题意,此题为双侧假设检验问题(1)原假设:;备择假设:(2)构造统计量:,得(3)由于,则查表得:(4),,所以拒绝原假设,即在0.05的显著水平下没有达到2.2分钟的标准。\n2、某商店为解决居民对某种商品的需要,调查了100户住户,得出每月每户平均需要量为10千克,样本方差为9。若这个商店供应10000户,求最少需要准备多少这种商品,才能以95%的概率满足需要?解:设每月每户至少准备ð查表得,ð若供应10000户,则需要准备104400kg。二、简答题(每小题25分,共50分)1.解释相关关系的含义,说明相关关系的特点。答:变量之间存在的不确定的数量关系为相关关系。相关关系的特点:一个变量的取值不能由另一个变量唯一确定,当变量x取某个值时,变量y的取值可能有几个;变量之间的相关关系不能用函数关系进行描述,但也不是无任何规律可循。通常对大量数据的观察与研究,可以发现变量之间存在一定的客观规律。2.为什么对总体均值进行估计时,样本容量越大,估计越精确?答:因为总体是所要认识的研究对象的全体,它是具有某种共同性质或特征的许多单位的集合体.总体的单位数通常用N来表示,N总是很大的数.样本是总体的一部分,它是从总体中随机抽取出来、代表总体的那部分单位的集合体.样本的单位数称为样本容量,通常用n表示。样本容量n越大,就越接近总体单位数N,样本均值就越接近总体均值,对总体均值进行估计时,估计越精确。第三组:一、计算题(每小题25分,共50分)\n1、根据下表中Y与X两个变量的样本数据,建立Y与X的一元线性回归方程。YX51015201200081018140343010fx34111028解:设x为自变量,y为因变量,一元线性回归设回归方程为y===回归方程为y=150.213-1.538x2、每包重量(克)包数(包)fxxfx-(x-)2f148—14910148.51485-1.832.4149—15020149.52990-0.812.8150—15150150.575250.22.0151—15220151.530301.228.8合计100--15030--76.0要求:(1)计算该样本每包重量的均值和标准差;(2)以99%的概率估计该批茶叶平均每包重量的置信区间(t0.005(99)≈2.626);(3)在ɑ=0.01的显著性水平上检验该制造商的说法是否可信(t0.01(99)≈2.364)(4)以95%的概率对这批包装茶叶达到包重150克\n的比例作出区间估计(Z0.025=1.96);(写出公式、计算过程,标准差及置信上、下保留3位小数)二、简答题(每小题25分,共50分)1.区间估计与点估计的结果有何不同?答:点估计是使用估计量的单一值作为总体参数的估计值;区间估计是指定估计量的一个取值范围都为总体参数的估计。2.统计调查的方法有那几种?答:三种主要调查方式:普查,抽样调查,统计报表。实际中有时也用到重点调查和典型调查。\n第四组:一、计算题(每小题25分,共50分)1、假定某化工原料在处理前和处理后取样得到的含脂率如下表:处理前0.1400.1380.1430.1420.1440.137处理后0.1350.1400.1420.1360.1380.140假定处理前后含脂率都服从正态分布,问处理后与处理前含脂率均值有无显著差异。解:根据题中数据可得:,由于<30,且总体方差未知,所以先用F检验两总体方差是否存在差异。(1)设:;则F=由,查F分布得,接受,即处理前后两总体方差相同。(2)设,则T=,T=1.26<=2.2281接受,即处理前后含脂率无显著差异。\n2、一种新型减肥方法自称其参加者在第一个星期平均能减去至少8磅体重.由40名使用了该种方法的个人组成一个随机样本,其减去的体重的样本均值为7磅,样本标准差为3.2磅.你对该减肥方法的结论是什么?(α=0.05,μα/2=1.96,μα=1.647)二、简答题(每小题25分,共50分)1.解释抽样推断的含义。答:简单说,就是用样本中的信息来推断总体的信息。总体的信息通常无法获得或者没有必要获得,这时我们就通过抽取总体中的一部分单位进行调查,利用调查的结果来推断总体的数量特征。2.时期数列与时点数列有哪些不同的特点?答:时期数列具有以下特点:(1)数列具有连续统计的特点;(2)数列中各个指标数值可以相加;(3)数列中各个指标值大小与所包括的时期长短有直接关系。时点数列具有以下特点:(1)数列指标不具有连续统计的特点;(2)数列中各个指标值不具有可加性;(3)数列中每个指标值的大小与其时间间隔长短没有直接联系。第五组:一、计算题(每小题25分,共50分)1、某商业企业商品销售额1月、2月、3月分别为216,156,180.4万元,月初职工人数1月、2月、3月、4月分别为80,80,76,88人,试计算该企业1月、2月、3月各月平均每人商品销售额和第一季度平均每月人均销售额。(写出计算过程,结果精确到0.0001万元\人)解:依题意,计算如下:(人)2、下表中的数据是主修信息系统专业并获得企业管理学士学位的学生,毕业后的月薪(用y表示)和他在校学习时的总评分(用x表示)的回归方程。总评分月薪/美元总评分月薪/美元\n2.628003.230003.431003.534003.635002.93100解:2.628006.76728078400003.4310011.561054096100003.6350012.9612600122500003.2300010.24960090000003.5340012.2511900115600002.931008.4189909610000=19.2=18900=62.18=6091059870000设==581.08=18900/6-581.08*19.2/6=1290.54于是二、简答题(每小题25分,共50分)1.为什么要计算离散系数?答:离散系数是指一组数据的标准差与其相应得均值之比,也称为变异系数。\n对于平均水平不同或计量单位不同的不同组别的变量值,是不能用方差和标准差比较离散程度的。为消除变量值水平高低和计量单位不同对离散程度测度值的影响,需要计算离散系数。离散系数的作用主要是用于比较不同总体或样本数据的离散程度。离散系数大的说明数据的离散程度也就大,离散系数小的说明数据的离散程度也就小。1.简述算术平均数、几何平均数、调和平均数的适用范围。答:几何平均数主要适用于比率的平均。一般地说,如果待平均的变量x与另外两个变量f和m有fx=m的关系时,若取f为权数,应当采用算术平均方法;若取m为权数,应当采用调和平均方法。要求:1.独立完成,作答时要写明题型、题号;2.作答方式:手写作答或电脑录入,使用A4格式白纸;3.提交方式:以下两种方式任选其一,1)手写作答的同学可以将作业以图片形式打包压缩上传;2)提交电子文档的同学可以将作业以word文档格式上传;4.上传文件命名为“中心-学号-姓名-科目.rar”或“中心-学号-姓名-科目.doc”;5.文件容量大小:不得超过20MB。查看更多