统计学培训课件

统计学培训课件

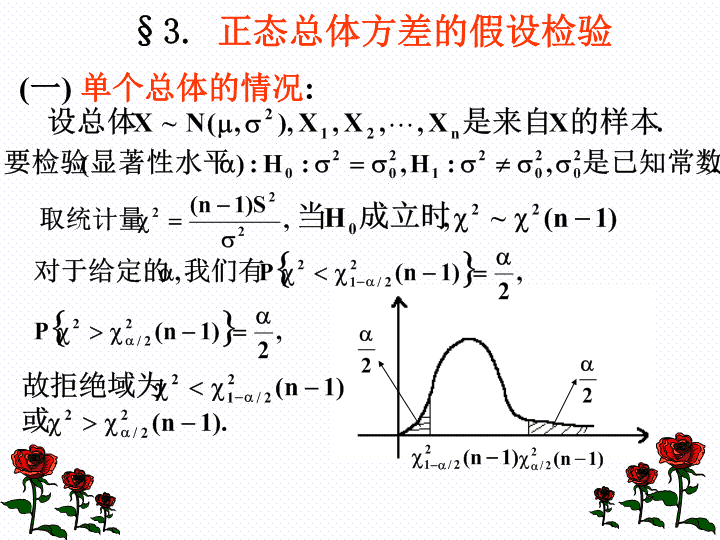
统计学南京航空航天大学\n目录随机样本抽样分布点估计估计量的评选标准区间估计正态总体均值与方差的区间估计(0-1)分布参数的区间估计单侧置信区间假设检验正态总体均值的假设检验正态总体方差的假设检验分布的拟合检验秩和检验\n§3.正态总体方差的假设检验(一)单个总体的情况:\n例1.某厂生产的某种型号的电池,其寿命长期以来服从方差2=5000(小时2)的正态分布,现有一批这种电池,从它的生产情况来看,寿命的波动性有所改变.现随机取26只电池,测得其寿命样本方差为s2=9200(小时2).问根据这一数据能否推断这批电池寿命的波动性较以往的有显著的变化(取=0.02)?\n(二)两个总体的情况:\n\n例2.在平炉上进行一项试验以确定改变操作方法的建议是否会增加钢的得率,试验是在同一只平炉上进行的.每炼一炉钢时除操作方法外,其它条件都尽可能做到相同.先用标准方法炼一炉,然后手建议的方法炼一炉,以后交替进行,各炼了10炉,其得率分别为:标准方法:78.172.476.274.377.478.476.075.576.777.3新方法:79.181.077.379.180.079.179.177.380.282.1设这两个样本相互独立,且分别来自正态总体N(1,12)和N(2,22),1,2,12,22均未知.试对数据检验假设(=0.01),H0:12=22,H1:12≠22.\n\n§4.分布的拟合检验一.2检验法:1.基本思想:\n\n注意:2检验法是基于以上定理下得到的,所以在使用时必须注意到n要足够大,以及npi不太小.根据实践,要求样本容量n不小于50,以及每一个npi都不小于5,而且最好是在5以上,否则应适当地合并Ai.\n例1.在一个实验中,每隔一定时间观察一次由某种铀所放射的到达计数器上的粒子数x,共观察了100次,得结果如下:i0123456789101112fi15161726119921210AiA0A1A2A3A4A5A6A7A8A9A10A11A12其中fi是观察到有i个粒子的次数.从理论上考虑知,x应服从参数为的泊松分布().问:理论是否符合实际?(取=0.05).即在水平0.05下检验假设:H0:总体X~().\n\n\n(二).偏度,峰度检验:\n\n\n\n§5.秩和检验1.定义:设x为一总体,将一容量为n的样本观察值按自大到小的次序编号排列成x(1)0;H0:a=0,H1a≠0.分析:当H0成立时,X和Y的分布相同,每一个Xi和Yj出现在混合样本中的某一位置上的可能性是相同的.考虑样本容量较小的样本X.直观上,X1,X2,…,Xn1集中在混合样本中的左端或集中在混合样本中的右端的可能性都有比较小.换句话说,R1比较小(接近1+2+…+n1)或比较大(接近(n2+1)+(n2+2)+…+(n2+n1))的可能性都比较小.因此,当R1的观察值r1过分大或过分小时,我们拒绝H0.\n\n注:对于临界点的求法:\n\n