统计学笔记全

统计学笔记全

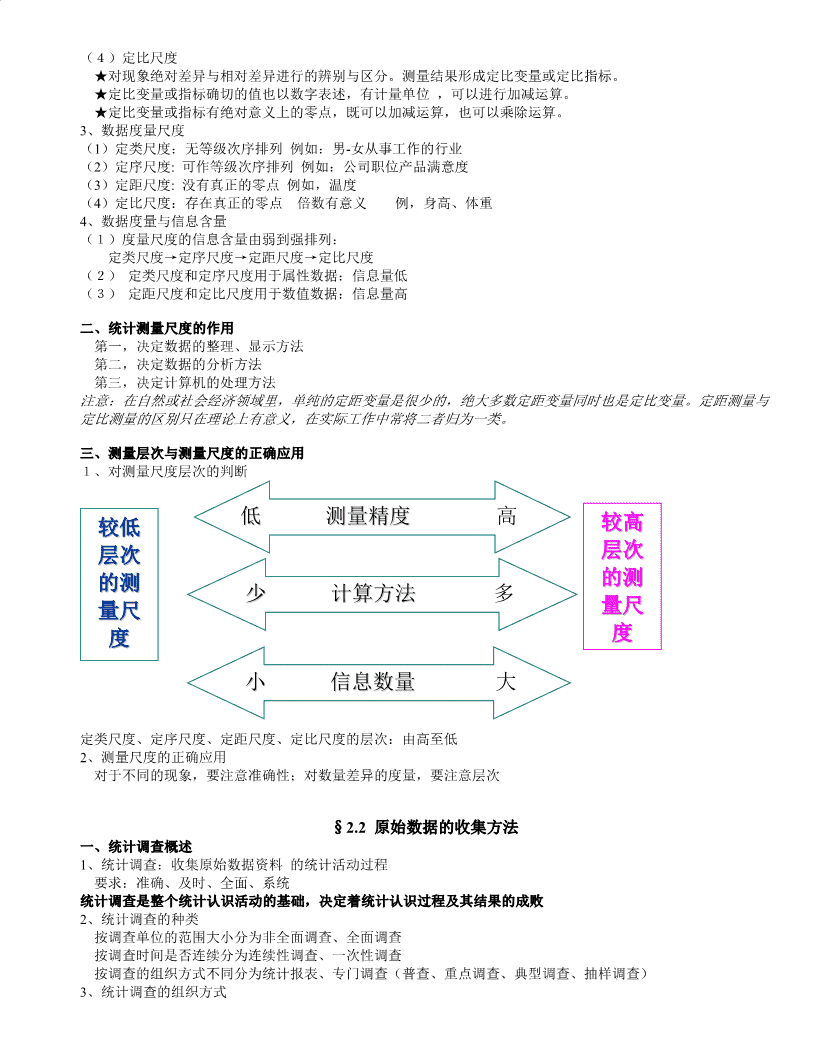
第一章总论第一节统计学概述一、什么是统计学1、统计学的定义：统计学是一门关于数据的科学，是一门关于数据的收集、整理、分析、解释和推断的科学。2、统计的三种含义：统计工作对现象的数量进行搜集、整理和分析的活动过程统计资料通过统计实践活动取得的说明对象某种数量特征的数据统计学是关于数据的一门科学三者之间的关系：统计工作与统计资料是工作与工作成果关系，三者之间是实践与理论关系3、统计学的研究对象：一切自然与社会现象总体的数量特征及其相互关系特点：数量性、总体性、变异性4、统计学的研究方法大量观察法、统计指标法、统计推断法二、统计学的产生与发展1、古典统计学（17世纪中——18世纪中）：记述学派和政治算术学派2、近代统计学（18世纪末——19世纪末）：数量统计学派和社会统计学派3、现代统计学（20世纪至今）三、统计学的分类1、理论统计学：研究的内容是统计的一般理论和方法描述统计学用图形、表格和数值方法来汇总数据的统计学。推断统计学用样本数据对总体的某些特征进行估计和假设检验的统计学。2、应用统计学：研究的内容是运用于某一特定领域的统计问题第二节统计学的基本概念一、统计总体与总体单位1、统计总体：由客观存在的、在同一性质基础上结合起来的许多个别单位所形成的集合。具有大量性、同质性和变异性等特点2、总体单位：指构成总体的个体即每一个单位。总体由总体单位构成，要认识总体必须从总体单位开始，总体是统计认识的对象。总体或总体单位的区分不是固定的：同一个研究对象，在一种情况下是总体，在另一种情况下可能成了总体单位。3、统计总体的种类（1）有限总体：指所包含的单位数目有限的总体无限总体：指所包含的单位数目无限的总体（2）大总体小总体：指大总体的各组成部分（3）可加总体：指总体单位可以合计的总体不可加总体：指总体单位不能合计的总体二、标志与变量1、标志：指总体单位所具有的属性和特征，标志的具体表现称为标志值。（1）品质标志：是表明事物“质”的特性的标志数量标志：是表明事物“量”的特性的标志其中，可变的数量标志又被叫作变量统计研究是从登记标志开始，并通过对标志的综合来反映总体的数量特征，因此标志是统计研究的起点。（2）总体单位标志分为不变标志（标志表现无差异）和变异标志（标志表现有差异）\n2、变量的种类确定性变量：指受确定性因素影响的变量随机变量：指受随机因素影响的变量连续型变量：在一个区间内可以连续不断取值的变量离散型变量：其一切可能取值都以整数形式出现，并可以一一列举的变量三、指标与指标体系1、统计指标：反映社会经济现象总体数量特征的概念及其具体数值构成要素：时间限制、空间限制、指标名称、具体数值、计量单位性质：数量性、具体性、综合性2、标志与指标的联系与区别：联系：（1）标志是总体指标的来源和基础，指标则是标志的综合。（2）数量标志与指标之间存在着变换关系。区别：（1）标志是说明总体单位特征的，指标则是说明统计总体数量特征的。（2）有的标志用数值表示，有的标志用文字表示，而指标都是用数值表示的。3、统计指标的分类（１）按表现形式分：总量指标、相对指标、平均指标（２）按内容特征分：数量指标、质量指标数量指标：反映的是所研究总体的规模和水平，其大小取决于总体单位数目的多少及其标志水平的高低。质量指标：反映的是与总体单位数相对应的标志的平均水平或其它数量对比关系。（３）按计量单位分：实物指标、价值指标、劳动指标（４）按时间特征分：时期指标、时点指标４、统计指标体系：具有某种内在联系的一系列统计指标所构成的整体作用：全面、综合地对客观事物进行描述、分析。５、样本：由总体的部分单位组成的集合第二章统计数据的收集§2.1统计测量尺度一、统计测量尺度的概念与种类１、统计测量：运用某种方法使自然或社会经济现象量化。测量结果：形成变量或指标分类、标识2、统计测量尺度的种类（１）定类尺度★按现象性质差异进行的辨别与区分。测量结果形成定类变量或定类指标。★定类变量或指标确切的值是以文字表述的，可以用数值标识，但仅起标签作用。★定类变量或指标的各类别间是平等的，没有高低、大小、优劣之分。（２）定类尺度★对现象顺序差异进行的辨别与区分。测量结果形成定序变量或定序指标。★定序变量或指标确切的值是以文字表述的，也可以用数值标识，也仅起标签作用。★定序变量或指标各类别间有高低优劣之分，不能随意排列，但差异无法准确计量。（３）定距尺度★按现象绝对数量差异进行的辨别与区分。测量结果形成定距变量或定距指标。★定距变量或指标的值以数字表述，有计量单位，可以进行加减运算。★定距变量或指标各类别间自然有大小之分，但没有绝对的零点，不能进行乘除运算。\n（４）定比尺度★对现象绝对差异与相对差异进行的辨别与区分。测量结果形成定比变量或定比指标。★定比变量或指标确切的值也以数字表述，有计量单位，可以进行加减运算。★定比变量或指标有绝对意义上的零点，既可以加减运算，也可以乘除运算。3、数据度量尺度（1）定类尺度：无等级次序排列例如：男-女从事工作的行业（2）定序尺度:可作等级次序排列例如：公司职位产品满意度（3）定距尺度:没有真正的零点例如，温度（4）定比尺度：存在真正的零点倍数有意义例，身高、体重4、数据度量与信息含量（１）度量尺度的信息含量由弱到强排列：定类尺度→定序尺度→定距尺度→定比尺度（２）定类尺度和定序尺度用于属性数据：信息量低（３）定距尺度和定比尺度用于数值数据：信息量高二、统计测量尺度的作用第一，决定数据的整理、显示方法第二，决定数据的分析方法第三，决定计算机的处理方法注意：在自然或社会经济领域里，单纯的定距变量是很少的，绝大多数定距变量同时也是定比变量。定距测量与定比测量的区别只在理论上有意义，在实际工作中常将二者归为一类。三、测量层次与测量尺度的正确应用１、对测量尺度层次的判断较低低测量精度高较高层次层次的测的测少计算方法多量尺量尺度度小信息数量大定类尺度、定序尺度、定距尺度、定比尺度的层次：由高至低2、测量尺度的正确应用对于不同的现象，要注意准确性；对数量差异的度量，要注意层次§2.2原始数据的收集方法一、统计调查概述1、统计调查：收集原始数据资料的统计活动过程要求：准确、及时、全面、系统统计调查是整个统计认识活动的基础，决定着统计认识过程及其结果的成败2、统计调查的种类按调查单位的范围大小分为非全面调查、全面调查按调查时间是否连续分为连续性调查、一次性调查按调查的组织方式不同分为统计报表、专门调查（普查、重点调查、典型调查、抽样调查）3、统计调查的组织方式\n（１）统计报表：指按照国家统一规定的各项要求，自下而上地定期向国家和主管部门报送基本统计资料的一种报告制度优点：能保证统计资料的全面性和连续性；能保证统计资料的统一性和及时性；能满足各级部门对统计资料的需要局限：统计报表过多会增加基层负担；有可能由于虚报瞒报而影响统计资料质量（２）普查：指国家为详尽了解某项重要的国情国力而专门组织的一次性全面调查作用：可以为抽样调查提供抽样框；可以收集统计报表所不能提供的反映重大国情国力的基本统计信息局限：由于需要大量的人力、物力和财力，不宜经常进行（３）重点调查：为了解总体基本情况，在调查对象中只选择一部分重点单位进行调查的一种非全面调查组织方式作用：能以较少的投入和较快的速度取得总体基本情况及变动趋势的资料局限：只适用于客观存在着重点单位的情况（４）典型调查：在对调查对象有一定了解的基础上，有意识地选择少数典型单位进行调查的一种非全面调查组织方式作用：一定条件下能估计总体指标数值；可以补充全面调查的不足；可以用来研究新生事物局限：不能确定推断的把握程度，无法计算和控制推断误差（５）抽样调查：按照随机原则从调查对象中抽取一部分样本单位进行调查，再用样本资料推断把握总体的数量特征的一种非全面调查组织方式特点：按随机原则抽取样本单位；目的是推断总体的数量特征；抽样误差可以事先计算并控制优点：能用较少的人力、物力和时间达到全面调查的目的；调查资料的准确性较高、受人为干扰的可能性较小４、统计调查的主要技术方法观察记录法、报告法、访问调查法二、统计调查方案１、统计调查方案：用来指导整个调查工作的纲领性文件，是统计设计在统计调查阶段的具体化２、基本内容：调查目的；调查对象与调查单位；调查项目与调查表；调查时间；制定调查工作的组织实施计划。三、问卷设计１、问卷调查：主要指非政府性统计机构或个人所从事的对人的主观意见的调查工作，也称作民意调查或民意测验调查问卷的基本格式：表头（说明词：解释调查意义、表达感激之情等）；表体（主题问句：被调查者基本情况、调查项目）；表脚（作业记录：时间、操作者等）2、调查对象：被调查现象的物质承担者指，是总体在调查阶段的具体化调查单位：指构成调查对象的每一个总体单位3、调查问卷的问题类型：封闭式问题、开放式问题4、问卷调查的基本要求主题明确、提问科学、逻辑性强、容量适度§2.3次级资料的收集一、次级资料指已经被收集、加工整理成型的数据信息二、次级资料的主要收集渠道：⒈查阅公开出版物；⒉向政府统计机构咨询；⒊向其他机构咨询；⒋网上查询。§2.4统计调查误差一、调查误差指收集来的数据资料与真实情况间的差异二、调查误差的种类１、登记误差：由于人的主观故意或失误而产生的误差，理论上它可以用某种方法加以消除２、代表性误差（随机误差）：由部分单位数值来推断总体数值所产生的误差，它不可以消除，但可以加以控制\n第三章统计数据的整理与显示§3.1统计整理与统计分组一、统计整理的意义和步骤１、统计整理：将统计调查得到的原始资料进行科学的分组和汇总形成综合统计资料的工作过程２、统计整理的内容统计数据的处理：统计资料的分组、汇总及制表统计数据的管理：数据的传输、贮存、更新及输出３、统计整理的步骤制定统计整理方案、对原始资料进行审核、数据处理、制作统计表和统计图二、统计整理的基本方法（一）统计分组：将总体中所有单位按一定的标志分为性质不同但又有联系的若干部分的过程１、统计分组的作用划分社会经济现象的类型反映社会经济现象的内部结构和比例关系揭示社会经济现象之间的相互依存关系２、统计分组的程序选择分组标志、确定分组体系、总体单位归类３、统计分组的原则科学性、完备性、互斥性（二）分组体系：指同时使用两个以上标志分组时，分组标志的组合形式。平行分组体系、交叉分组体系§3.2分布数列的编制一、分布数列的定义及种类１、分布数列：将总体各单位按某个标志分成若干组，列出各组的总体单位数或各组在总体中所占的比重而形成的数列构成要素：分组标志的具体表现、各组的次数或频率分类：品质数列单值数列等距数列变量数列组距数列异距数列二、变量数列的编制１、单值数列：指每个组值只用一个具体的变量值表现的数列编制条件：变量是离散变量；变量的不同取值个数较少２、组距数列：指每个组的变量值用一个区间来表现的变量数列编制条件：变量是连续变量；或：总体单位数较多，变量不同取值个数也较多的离散变量。分类：等距数列、异距数列３、相关概念组限：指每组两端表示各组界限的变量值，各组的最小值为下限，最大值为上限组距：每组变量值变动区间的长度，为上下限之差组中值：每组变量取值范围的中点数值上限下限组中值=2相邻组距缺上限开口组组中值＝下限2开口式组距数列组中值的计算：相邻组距缺下限开口组组中值＝上限-2\n４、编制等距数列步骤（１）求变异全距（２）确定组距及组数:R≤组距(d)×组数（m)确定组距的原则：要能区分各组的性质差异要能反映总体资料的分布特征为方便计算，尽可能为5或10的整数倍计算组数（组数不宜过多，也不宜太少）RRm（当（当的结果为整数）的结果为整数）ddRRm1（当（当的结果为小数）的结果为小数）dd（3）确定组限对于离散变量，相邻组组限可以间断，也可重叠；对于连续变量，相邻组组限必须重叠；符合“上组限不计入”原则；首末两组可使用“××以下”及“××以上”的开口组。（４）计算次数三、累计次数与累计频率1、频率：各组单位数占总体单位总数的比重2、累计次数（频率）向上累计：从变量值高的组开始，将各组次数（频率）逐次向变量值低的组累计向下累计：从变量值低的组开始，将各组次数（频率）逐次向变量值高的组累计§3.3统计图表一、统计图以点、线条、面积等方法描述、显示统计数据的形式组成：坐标系、图形、图例二、统计表以纵横交叉的线条所形成的表格来表现统计资料的形式1、常用结构：总标题、主词栏、宾词栏、数据栏2、统计表的编制规则选择合适的总标题；主词栏与宾词栏要各归其位，相互对应；表的上、下端用粗线或双线封口，左右两端一般不封口；可在各列的文字标题下面设置编号加以标识；数据栏不能有空白。\n第四章变量数列分析§4.1集中趋势的测定一、集中趋势的涵义指总体中各单位的次数分布从两边向中间集中的趋势，用平均指标来反映。测定集中趋势的意义：可以反映现象总体的客观规定性；可以对比同类现象在不同的时间、地点和条件下的一般水平；可以分析现象之间的依存关系。二、平均指标的种类及计算方法（一）算术平均数1、简单算术平均数：适用于总体资料未经分组整理、尚为原始资料的情况NXiXXX12Ni1XNN2、加权算术平均数：适用于总体资料经过分组整理形成变量数列的情况mXifiXfXfXf1122mmi1Xmfff12mfii1（说明若资料为组距数列，则应取各组的组中值作为该组的代表值用于计算）（1）权数：指变量数列中各组标志值出现的次数，是变量值的承担者，反映了各组的标志值对平均数的影响程度绝对权数：表现为次数、频数、单位数相对权数：表现为频率、比重算术平均数的计算取决于变量值和权数的共同作用：变量值决定平均数的范围；权数则决定平均数的位置3、算术平均数的数学性质变量值与其算术平均数的离差之和衡等于零；变量值与其算术平均数的离差平方和为最小，（二）调和平均数是总体各单位标志值倒数的算术平均数的倒数，又叫倒数平均数1、简单调和平均数：适用于总体资料未经分组整理、尚为原始资料的情况mmXH1111XXXX12m2、加权调和平均数：适用于总体资料经过分组整理形成变量数列的情况m1m2mmmXHmmm112mmXXXX12m3、调和平均数的应用：当已知各组变量值和标志总量时，作为算术平均数的变形使用。m设mXf,则XH1mXXfXfX1fXfX\n（三）几何平均数是N项变量值连乘积的开N次方根1、应用：用于计算现象的平均比率或平均速度2、应用的前提条件各个比率或速度的连乘积等于总比率或总速度；相乘的各个比率或速度不为零或负值。3、简单几何平均数：适用于总体资料未经分组整理尚为原始资料的情况NNXGX1X2XNX4、加权几何平均数：适用于总体资料经过分组整理形成变量数列的情况mmfifmfffmifii112XGX1X2Xmi1Xii1同一资料，xxxHG（四）中位数将总体各单位标志值按大小顺序排列后，指处于数列中间位置的标志值。不受极端数值的影响，在总体标志值差异很大时，具有较强的代表性。1、未分组数据：首先排序，再按数据n为奇数和偶数进行计算中位数2、单值数据：首先排序，然后根据中位数的位次对照累积计数确定中位数所在组，该组的标志值即为中位数3、组距数据fSm12MLdef（五）众数m指总体中出现次数最多的变量值，它不受极端数值的影响，用来说明总体中大多数单位所达到的一般水平。1、单值数据2、组距数据1MLdo12（六）数据分布表明数据是如何分布的偏态与对称左偏:均值<中位数右偏:均值>中位数对称(零偏度)：均值=中位数（七）百分位数第p个百分位数是这样的数值：至少有p%个数值跟它一样大或比它小；至少有(100－p)%个数值跟它一样大或比它大。四分位数：通常将数据分成四个部分是合乎需要的，每一部分大约包括1/4或25%的数据，分位点称为四分位数。§4.2离中趋势的测定一、离中趋势的涵义指总体中各单位标志值背离分布中心的规模或程度，用标志变异指标来反映。1、变异指标值越大，平均指标的代表性越小；反之，平均指标的代表性越大2、测定离中趋势的意义用来衡量和比较平均数代表性的大小；用来反映社会经济活动过程的均衡性和节奏性；用来测定变量数列次数分布较正态分布的偏离程度。二、标志变异指标的种类及计算\n（一）全距指所研究的数据中，最大值与最小值之差1、计算公式RXXmaxmin2、全距的特点优点:计算方法简单、易懂；缺点:易受极端数值的影响，不能全面反映所有标志值差异大小及分布状况，准确程度差（二）平均差：是各个数据与其算术平均数的离差绝对值的算术平均数1、简单平均差：适用于未分组资料NXXXXXiX1Ni1ADNN2、加权平均差：适用于分组资料mXXfXXfXiXfi11mmi1ADmff1mfii13、平均差的特点优点:不易受极端数值的影响，能综合反映全部单位标志值的实际差异程度；缺点:用绝对值的形式消除各标志值与算术平均数离差的正负值问题，不便于作数学处理和参与统计分析运算。（三）标准差：是各个数据与其算术平均数的离差平方的算术平均数的开平方根；标准差的平方又叫作方差1、简单标准差：适用于未分组资料N2XiXi1N2、加权标准差：适用于分组资料m2XiXfii1mfii13、标准差的特点不易受极端数值的影响，能综合反映全部单位标志值的实际差异程度；用平方的方法消除各标志值与算术平均数离差的正负值问题，可方便地用于数学处理和统计分析运算.（四）变异系数AD1、平均差系数VAD100﹪X标准差系数V100﹪2、应用X用来对比不同水平的同类现象;标准差系数小的总体，其平均数的代表性大；反之，亦然。\n三、是非标志的标准差及方差1、是非标志：指总体中全部单位只具有“是”或“否”、“有”或“无”两种表现形式的标志，又叫交替标志分组单位数变量值N1具有某一属性1不具有某一属性N00合计—N2、成数：指是非标志总体中具有某种表现或不具有某种表现的单位数占全部总体单位总数的比重具有某种标志表现的单位数所占的成数：NP1NPQ1N不具有某种标志表现的单位数所占的成数：Q0N3、是非标志总体的指标2均值：XP；标准差：PQ；方差：P(1P)；标准差系数：VPPP第五章抽样推断§5.1抽样方案的设计一、抽样估计的意义和一般步骤（一）抽样估计的定义按照随机原则从调查对象中抽取一部分单位进行调查，并以调查结果对总体数量特征作出具有一定可靠程度的估计与推断，从而认识总体的一种统计方法。（二）抽样估计的特点按随机原则抽取样本单位目的是推断总体的数量特征抽样推断的结果具有一定的可靠程度，抽样误差可以事先计算并控制（三）抽样估计的应用不可能进行全面调查时不必要进行全面调查时来不及进行全面调查时对全面调查资料进行补充修正时（四）抽样估计的步骤设计抽样方案、抽取样本单位、收集样本数据、计算样本统计量、推断总体参数（五）抽样估计的基本概念1、样本容量：从总体中抽出的部分单位的集合（n)2、样本个数：从一个总体中可能抽取多少个样本3、总体参数：指被估计的总体指标NmXiXifii1i1（1）总体平均数（总体均值）X或XmNfii1\nNm1212（2）总体单位标志值的标准差NXiX或mXiXfii1i1fii1Nm212212XiX或mXiXfi（3）总体单位标志值的方差Ni1i1fii1NN10（4）总体成数P,Q1PNN（5）总体是非标志的标准差P1PPQP2（6）总体是非标志的方差PP1PPQ4、样本指标：指根据样本单位的标志值计算的用以估计和推断相应总体指标的综合指标，又被称为估计量或统计量。nm（1）样本平均数（样本均值）xxfiiii1i1x或xmnfii1nm1212（2）样本单位标志值的标准差sxix或smxixfin1i1i1fi1i1nm212212sxix或smxixfi（3）样本单位标志值的方差n1i1f1i1ii1nn10（4）样本成数p,q1pnnnnsp1ppq（5）样本单位是非标志的标准差pn1n1（6）样本单位是非标志的方差2nnsp1ppqp二、抽样方案设计的基本准则n1n1随机原则、抽样误差最小、费用最少三、抽样方案设计的主要内容（一）编制抽样框抽样框：指包括全部抽样单位的名单框架，仅对有限总体而言主要形式：名单抽样框、区域抽样框、时间表抽样框\n（二）确定抽样方法1、重复抽样抽出个体→登记特征→放回总体→继续抽取2、不重复抽样抽出个体→登记特征→继续抽取（三）确定抽样组织方式1、简单随机抽样对总体单位逐一编号，然后按随机原则则直接从总体中抽出若干单位构成样本。应用：仅适用于规模不大、内部各单位标志值差异较小的总体2、类型抽样将总体全部单位分类，形成若干个类型组，然后从各类型中分别抽取样本单位组成样本。3、等距抽样将总体单位按某一标志排序，而后按一定的间隔抽取样本单位。4、整群抽样将总体全部单位分为若干“群”，然后随机抽取一部分“群”，被抽中群体的所有单位构成样本。确定抽样组织方式需考虑：调查对象的性质特点；对调查对象的了解程度（抽样框的特点）；抽样误差的大小；人力、财力和物力等条件的限制（四）确定样本容量1、n≥30，为大样本；n<30，为小样本2、确定适当样本容量的意义：若n过大，调查工作量增大，体现不出抽样调查的优越性；若n过小，抽样误差会增大，抽样推断就会失去价值。3、样本的可能数目：在考虑顺序的抽样条件下，从总体N中随机抽取n个样本单位共有多少种可能的抽选结果nn（1）重复抽样的可能样本数目PNNNNN（2）不重复抽样的可能样本数目CnNN1Nn1N§5.2抽样分布一、抽样分布样本统计量所有可能值的概率分布（一）平均数的抽样分布全部可能样本平均数的均值等于总体均值，即：E(x)X从非正态总体中抽取的样本平均数当n足够大时其分布接近正态分布。从正态总体中抽取的样本平均数不论容量大小其分布均为正态分布。1样本均值的标准差为总体标准差的。n2x~N(X,)n（二）比率的抽样分布全部可能样本比率的均值等于总体比率，即：E(p)P从非正态总体中抽取的样本比率，当n足够大时其分布接近正态分布。从正态总体中抽取的样本比率，不论容量大小其分布均为正态分布。1样本比率的标准差为总体标准差的。nP~N(P,P(1P)n)np5,n(1p)5二、抽样估计量的优良标准设为待估计的总体参数，为样本统计量，则的优良标准为：\n1、无偏性：指样本指标的均值应等于被估计的总体指标若E(ˆ)，则称为的无偏性估计量2、有效性：作为优良的估计量，除了满足无偏性的要求外，其方差应比较小若，则称为比更有效的估计量12123、一致性：指随着样本单位数n的增大，样本估计量将在概率意义下越来越接近于总体真实值若对于任意0，有limP{}1n4、抽样估计量的优良标准x为X的无偏、有效、一致估计量s为的无偏、有效、一致估计量n1p为P的无偏、有效、一致估计量三、抽样误差的概念指样本估计量与总体参数之间数量上的差异，仅指由于按照随机原则抽取样本而产生的代表性误差，不包括登记性误差和系统偏差说明：对于任何一个样本，其抽样误差都不可能测量出来；抽样误差的大小可以依据概率分布理论加以说明。四、抽样平均误差指每一个可能样本的估计值与总体指标值之间离差的平均数，即样本估计量的标准差M12xXxiMi1式中：为样本平均数的抽样平均误差；M为可能的样本数目；x为第i个可能样本的平均数；X为总体平x均数1、样本平均数的抽样平均误差重复抽样：2不重复抽样：22Nnnxx1nnnN1nN2、样本成数的抽样平均误差重复抽样：P1P不重复抽样：P1PNnP1Pnpp1nnN1nN3、关于总体方差的估计方法用过去同类问题全面调查或抽样调查的经验数据代替；用样本标准差s代替总体标准差，用s代替。pp4、影响抽样误差的因素总体各单位的差异程度；样本单位数的多少；抽样方法；抽样组织方式五、抽样极限误差指在一定的概率保证程度下，抽样误差不允许超过的某一给定范围，也称作允许误差。§5.3参数估计一、点估计指直接以样本指标来估计总体指标Xx,s,Pp优点：简单，具体明确缺点：无法控制误差，仅适用于对推断的准确程度与可靠程度要求不高的情况二、区间估计（一）区间估计的定义和原理\n指根据样本指标和抽样极限误差以一定的可靠程度推断总体指标的可能范围；其中，被推断的总体指标的下限与上限所包括的区间称为置信区间，估计的可靠程度也称为置信度。（二）总体平均数的区间估计1、表达式xXx，xx，其中Zxx或Xx,x2、步骤xx（1）计算样本平均数x22222(xx)2(xx)f（2）搜集总体方差的经验数据，或计算样本标准差s，即s,sn1f1（3）计算抽样平均误差s重复抽样时：x或＝nn22nsn不重复抽样时：(1)或＝(1)xnNnN（4）计算抽样极限误差ZxxxXx，xx（5）确定总体平均数的置信区间或Xx,xxx（三）总体成数的区间估计1、表达式pPp，pp或Pp,ppp，其中Zpp2、步骤n1（1）计算样本成数pn2（2）搜集总体方差的经验数据p（3）计算抽样平均误差pp(1p)重复抽样：或pnn12pnp(1p)n不重复抽样：(1)或＝(1)pnNn1N（4）计算抽样极限误差pZppPp，pp（5）确定总体成数的置信区间三、样本数目的确定或Ppp,pp㈠确定样本容量的意义考虑调查误差和调查费用两方面，确定样本容量㈡推断总体平均数所需的样本容量1、重复抽样222Zn22xx2、不重复抽样222NZNn22222NZNxx\n㈢推断总体成数所需的样本容量1、重复抽样2ZP1PP1Pn22PP2、不重复抽样2NZP1PNP1Pn222NpZP1PNpP1P㈣必要样本容量的影响因素总体方差的大小；允许误差范围的大小；概率保证程度；抽样方法；抽样的组织方式。第六章假设检验§6.1假设检验的一般问题一、假设检验的概念概念事先对总体参数或分布形式作出某种假设然后利用样本信息来判断原假设是否成立类型参数假设检验非参数假设检验特点采用逻辑上的反证法依据统计上的小概率原理二、假设检验的步骤（一）提出原假设和备择假设1、什么是原假设？研究者想收集证据予以反对的假设有等号,或表示为H02、什么是备择假设？研究者想收集证据予以支持的假设有不等号:,或表示为H1（二）确定适当的检验统计量1、用于假设检验问题的统计量2、选择统计量的方法与参数估计相同，需考虑是大样本还是小样本总体方差已知还是未知（三）规定显著性水平1、是一个概率值2、原假设为真时，拒绝原假设的概率被称为抽样分布的拒绝域3、表示为常用的值有0.01,0.05,0.10\n4、由研究者事先确定（四）计算检验统计量的值，作出统计决策1.计算检验的统计量2.根据给定的显著性水平，查表得出相应的临界值Z或Z/23.将检验统计量的值与水平的临界值进行比较4.得出接受或拒绝原假设的结论三、假设检验中的两类错误H0检验1、第一类错误（弃真错误）原假设为真时拒绝原假设实际情况会产生一系列后果决策第一类错误的概率为H0为真H0为假被称为显著性水平2、第二类错误（取伪错误）接受H0正确第二类错误(b)原假设为假时接受原假设第二类错误的概率为(Beta)拒绝H0第一类错误(a)正确3、错误和错误的关系和的关系就像翘翘板，小就大，大就小四、双侧检验和单侧检验（一）双侧检验与单侧检验(假设的形式)（课本P152）（二）双侧检验（原假设与备择假设的确定）1.双侧检验属于决策中的假设检验。也就是说，不论是拒绝H0还是接受H0，我们都必需采取相应的行动措施2.例如，某种零件的尺寸，要求其平均长度为10厘米，大于或小于10厘米均属于不合格3.建立的原假设与备择假设应为H0:=10H1:10（三）双侧检验（显著性水平与拒绝域）（课本P155）（四）单侧检验（原假设与备择假设的确定）检验研究中的假设1.将所研究的假设作为备择假设H12.将认为研究结果是无效的说法或理论作为原假设H0。或者说，把希望(想要)证明的假设作为备择假设3.先确立备择假设H1检验某项声明的有效性1.将所作出的说明(声明)作为原假设2.对该说明的质疑作为备择假设3.先确立原假设H0除非我们有证据表明“声明”无效，否则就应认为该“声明”是有效的（五）单侧检验（显著性水平与拒绝域）（课本P155）§6.2一个正态总体的参数检验检验的步骤陈述原假设H0陈述备择假设H1选择显著性水平选择检验统计量选择n给出临界值搜集数据计算检验统计量进行统计决策表述决策结果一、大样本的均值检验二、小样本的均值检验三、总体比率的假设检验\n方差分析一、方差分析的基本问题1、检验多个总体均值是否相等：通过对各观察数据误差来源的分析来判断多个总体均值是否相等2、变量一个定类尺度的自变量2个或多个(k个)处理水平或分类一个定距或比例尺度的因变量二、方差分析的基本思想和原理（一）基本概念1、因素或因子：所要检验的对象称为因子2、水平：因素的具体表现称为水平3、观察值：在每个因素水平下得到的样本值4、试验5、总体：因素的每一个水平可以看作是一个总体6、样本数据（二）两类误差1.随机误差在因素的同一水平(同一个总体)下，样本的各观察值之间的差异不同超市销售量的差异可以看成是随机因素的影响，或者说是由于抽样的随机性所造成的，称为随机误差2.系统误差在因素的不同水平(不同总体)下，各观察值之间的差异这种差异可能是由于抽样的随机性所造成的，也可能是由于颜色本身所造成的，后者所形成的误差是由系统性因素造成的，称为系统误差（三）两类方差组内方差因素的同一水平(同一个总体)下样本数据的方差组内方差只包含随机误差组间方差因素的不同水平(不同总体)下各样本之间的方差组间方差既包括随机误差，也包括系统误差（四）方差的比较1.如果不同水平对结果没有影响，那么在组间方差中只包含有随机误差，而没有系统误差。这时，组间方差与组内方差就应该很接近，两个方差的比值就会接近12.如果不同的水平对结果有影响，在组间方差中除了包含随机误差外，还会包含有系统误差，这时组间方差就会大于组内方差，组间方差与组内方差的比值就会大于13.当这个比值大到某种程度时，就可以说不同水平之间存在着显著差异第七章相关分析与回归分析§7.1相关分析一、相关分析概述（一）现象间的依存关系大致可以分成两种类型：1、函数关系：指现象间所具有的严格的确定性的依存关系2、相关关系：指客观现象间确实存在，但数量上不是严格对应的依存关系（二）相关关系的种类1、按涉及变量的多少：一元相关、多元相关2、按表现形式不同：直线相关、曲线相关3、按变化方向不同：正相关、负相关二、相关关系的测定（一）相关表：将现象之间的相互关系，用表格的形式来反映。1、简单相关表：适用于所观察的样本单位数较少，不需要分组的情况2、分组相关表：适用于所观察的样本单位数较多标志变异又较复杂，需要分组的情况\n（二）相关图：又称散点图，用直角坐标系的x轴代表自变量，y轴代表因变量，将两个变量间相对应的变量值用坐标点的形式描绘出来，用以表明相关点分布状况的图形。（三）相关系数：在直线相关的条件下，用以反映两变量间线性相关密切程度的统计指标，nxyxyr2222nx(x)ny(y)相关系数r的取值范围：-1≤r≤1（四）判定系数：是相关系数的平方；用来衡量回归方程对y的解释程度。2判定系数取值范围：0r1§7.2一元线性回归分析一、回归分析概述1、回归分析：指根据相关关系的数量表达式（回归方程式）与给定的自变量x，揭示因变量y在数量上的平均变化和求得因变量的预测值的统计分析方法。2、回归分析与相关分析的联系和区别联系：理论和方法具有一致性；无相关就无回归，相关程度越高，回归越好；相关系数和回归系数方向一致，可以互相推算。区别：相关分析中x与y对等，回归分析中x与y要确定自变量和因变量；相关分析中x、y均为随机变量，回归分析中只有y为随机变量；相关分析测定相关程度和方向，回归分析用回归模型进行预测和控制。3、回归分析的种类按自变量的个数分：一元回归、多元回归按回归曲线的形态分：线性回归、非线性回归二、一元线性回归模型1、yˆabx截距a表示在没有自变量x的影响时，其它各种因素对因变量y的平均影响；回归系数b表明自变量x每变动一个单位，因变量y平均变动b个单位。2、一元线性回归方程中参数a、b的确定——最小平方法nxyxyb22nx(x)yxabybxnn三、回归估计与预测1、点估计：对于给定的X值，求出Y平均值的一个估计值或Y的一个个别值的预测值。2、区间估计：对于给定的X值，求出Y的平均值的置信区间或Y的一个个别值的预测区间。