统计学 课后答案

统计学 课后答案

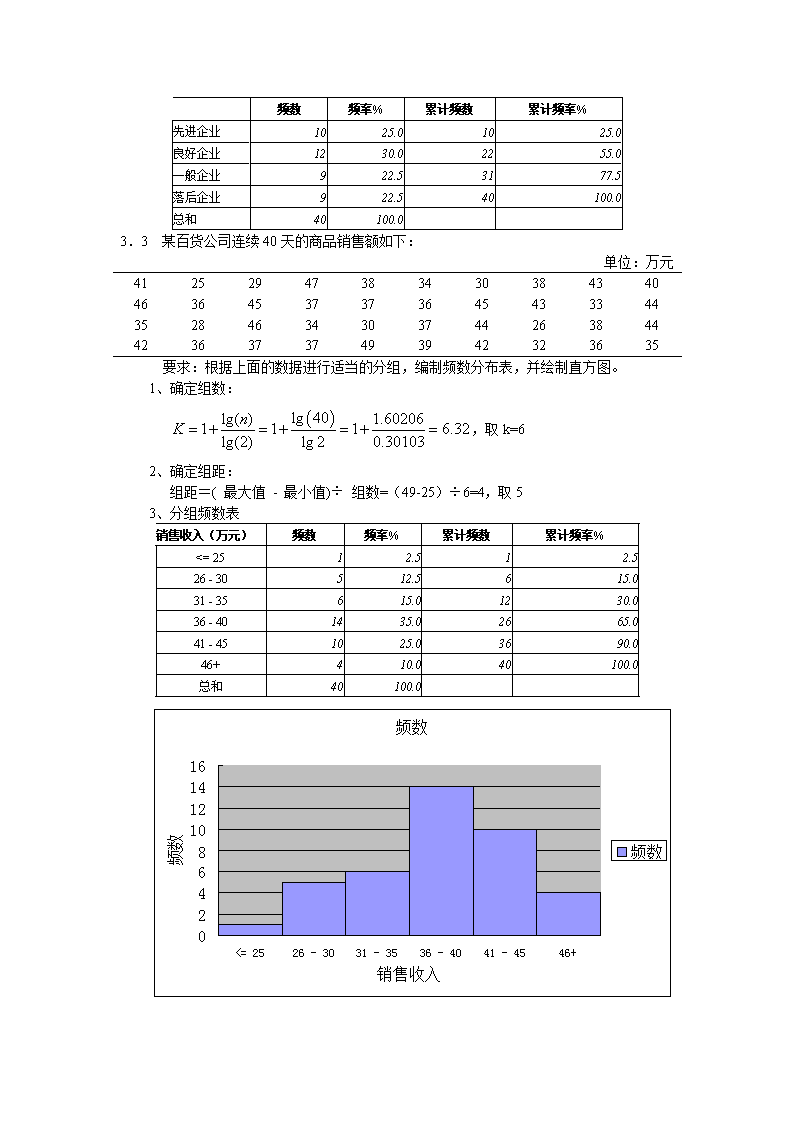
3．1为评价家电行业售后服务的质量，随机抽取了由100个家庭构成的一个样本。服务质量的等级分别表示为：A．好；B．较好；C一般；D．较差；E.差。调查结果如下：BECCADCBAEDACBCDECEEADBCCAEDCBBACDEABDDCCBCEDBCCBCDACBCDECEBBECCADCBAEBACEEABDDCADBCCAEDCBCBCEDBCCBC要求：(1)指出上面的数据属于什么类型。顺序数据(2)用Excel制作一张频数分布表。用数据分析——直方图制作：接收频率E16D17C32B21A14(3)绘制一张条形图，反映评价等级的分布。用数据分析——直方图制作：(4)绘制评价等级的帕累托图。逆序排序后，制作累计频数分布表：接收频数频率(%)累计频率(%)C323232B212153D171770E161686A1414100\n3．2某行业管理局所属40个企业2002年的产品销售收入数据如下：1521241291161001039295127104105119114115871031181421351251171081051101071371201361171089788123115119138112146113126要求：(1)根据上面的数据进行适当的分组，编制频数分布表，并计算出累积频数和累积频率。1、确定组数：，取k=62、确定组距：组距＝(最大值-最小值)÷组数=（152-87）÷6=10.83，取103、分组频数表销售收入频数频率%累计频数累计频率%80.00-89.0025.025.090.00-99.0037.5512.5100.00-109.00922.51435.0110.00-119.001230.02665.0120.00-129.00717.53382.5130.00-139.00410.03792.5140.00-149.0025.03997.5150.00+12.540100.0总和40100.0　　(2)按规定，销售收入在125万元以上为先进企业，115～125万元为良好企业，105～115万元为一般企业，105万元以下为落后企业，按先进企业、良好企业、一般企业、落后企业进行分组。\n　频数频率%累计频数累计频率%先进企业1025.01025.0良好企业1230.02255.0一般企业922.53177.5落后企业922.540100.0总和40100.0　　3．3某百货公司连续40天的商品销售额如下：单位：万元41252947383430384340463645373736454333443528463430374426384442363737493942323635要求：根据上面的数据进行适当的分组，编制频数分布表，并绘制直方图。1、确定组数：，取k=62、确定组距：组距＝(最大值-最小值)÷组数=（49-25）÷6=4，取53、分组频数表销售收入（万元）频数频率%累计频数累计频率%<=2512.512.526-30512.5615.031-35615.01230.036-401435.02665.041-451025.03690.046+410.040100.0总和40100.0　　\n3．4利用下面的数据构建茎叶图和箱线图。572929363123472328283551391846182650293321464152282143194220dataStem-and-LeafPlotFrequencyStem&Leaf3.001.8895.002.011337.002.2.003.133.003.5693.004.1233.004.6673.005.0121.005.7\nStemwidth:10Eachleaf:1case(s)3.5无3．6一种袋装食品用生产线自动装填，每袋重量大约为50g，但由于某些原因，每袋重量不会恰好是50g。下面是随机抽取的100袋食品，测得的重量数据如下：单位：g57464954555849615149516052545155605647475351485350524045575352514648475347534447505253474548545248464952595350435346574949445752424943474648515945454652554749505447484457475358524855535749565657534148要求：(1)构建这些数据的频数分布表。(2)绘制频数分布的直方图。(3)说明数据分布的特征。解：(1)根据上面的数据进行适当的分组，编制频数分布表，并计算出累积频数和累积频率。1、确定组数：，取k=6或72、确定组距：组距＝(最大值-最小值)÷组数=（61-40）÷6=3.5，取3或者4、5组距＝(最大值-最小值)÷组数=（61-40）÷7=3，3、分组频数表组距3，上限为小于频数百分比累计频数累积百分比有效40.00-42.0033.033.043.00-45.0099.01212.046.00-48.002424.03636.049.00-51.001919.05555.052.00-54.002424.07979.055.00-57.001414.09393.058.00+77.0100100.0合计100100.0　直方图：\n组距4，上限为小于等于频数百分比累计频数累积百分比有效<=40.0011.011.041.00-44.0077.088.045.00-48.002828.03636.049.00-52.002828.06464.053.00-56.002222.08686.057.00-60.001313.09999.061.00+11.0100100.0合计100100.0　直方图：\n组距5，上限为小于等于频数百分比累计频数累积百分比有效<=45.001212.012.012.046.00-50.003737.049.049.051.00-55.003434.083.083.056.00-60.001616.099.099.061.00+11.0100.0100.0合计100100.0　　直方图：\n分布特征：左偏钟型。3.7无3.8下面是北方某城市1——2月份各天气温的记录数据：-32-4-7-11-1789-614-18-15-9-6-105-4-96-8-12-16-19-15-22-25-24-19-8-6-15-11-12-19-25-24-18-17-14-22-13-9-60-15-4-9-32-4-4-16-175-6-5要求：(1)指出上面的数据属于什么类型。数值型数据(2)对上面的数据进行适当的分组。1、确定组数：，取k=72、确定组距：组距＝(最大值-最小值)÷组数=（14-（-25)）÷7=5.57，取5\n3、分组频数表温度频数频率%累计频数累计频率%-25--21610.0610.0-20--16813.31423.3-15--11915.02338.3-10--61220.03558.3-5--11220.04778.30-446.75185.05-9813.35998.310+11.760100.0合计60100.0　　(3)绘制直方图，说明该城市气温分布的特点。3.9无3.10无3.11对于下面的数据绘制散点图。x234187y252520301618解：\n3．12甲乙两个班各有40名学生，期末统计学考试成绩的分布如下：考试成绩人数甲班乙班优良中及格不及格361894615982要求：(1)根据上面的数据，画出两个班考试成绩的对比条形图和环形图。\n(2)比较两个班考试成绩分布的特点。甲班成绩中的人数较多，高分和低分人数比乙班多，乙班学习成绩较甲班好，高分较多，而低分较少。(3)画出雷达图，比较两个班考试成绩的分布是否相似。分布不相似。3.13无3.14已知1995—2004年我国的国内生产总值数据如下(按当年价格计算)：单位：亿元年份国内生产总值第一产业第二产业第三产业\n199519961997199819992000200120022003200458478.167884．674462．678345．282067．589468．197314．8.3．2．91199313844.214211．214552．414471．9614628．215411．816117．316928．120768．072853833613372233861940558449354875052980612747238717947204282302925174270382990533153360753918843721要求：(1)用Excel绘制国内生产总值的线图。(2)绘制第一、二、三产业国内生产总值的线图。(3)根据2004年的国内生产总值及其构成数据绘制饼图。\n\n第四章统计数据的概括性描述4．1一家汽车零售店的10名销售人员5月份销售的汽车数量(单位：台)排序后如下：24710101012121415要求：（1）计算汽车销售量的众数、中位数和平均数。(2)根据定义公式计算四分位数。(3)计算销售量的标准差。(4)说明汽车销售量分布的特征。解：Statistics汽车销售数量NValid10Missing0Mean9.60Median10.00Mode10Std.Deviation4.169Percentiles256.255010.007512.50\n4．2随机抽取25个网络用户，得到他们的年龄数据如下：单位：周岁19152925242321382218302019191623272234244120311723要求；(1)计算众数、中位数：1、排序形成单变量分值的频数分布和累计频数分布：网络用户的年龄FrequencyPercentCumulativeFrequencyCumulativePercentValid1514.014.01614.028.01714.0312.01814.0416.019312.0728.02028.0936.02114.01040.0\n2228.01248.023312.01560.02428.01768.02514.01872.02714.01976.02914.02080.03014.02184.03114.02288.03414.02392.03814.02496.04114.025100.0Total25100.0　　从频数看出，众数Mo有两个：19、23；从累计频数看，中位数Me=23。(2)根据定义公式计算四分位数。Q1位置=25/4=6.25，因此Q1=19，Q3位置=3×25/4=18.75，因此Q3=27，或者，由于25和27都只有一个，因此Q3也可等于25+0.75×2=26.5。(3)计算平均数和标准差；Mean=24.00；Std.Deviation=6.652(4)计算偏态系数和峰态系数：Skewness=1.080；Kurtosis=0.773(5)对网民年龄的分布特征进行综合分析：分布，均值=24、标准差=6.652、呈右偏分布。如需看清楚分布形态，需要进行分组。为分组情况下的直方图：\n为分组情况下的概率密度曲线：分组：1、确定组数：，取k=62、确定组距：组距＝(最大值-最小值)÷组数=（41-15）÷6=4.3，取53、分组频数表网络用户的年龄(Binned)FrequencyPercentCumulativeFrequencyCumulativePercentValid<=1514.014.016-20832.0936.021-25936.01872.026-30312.02184.031-3528.02392.036-4014.02496.041+14.025100.0Total25100.0　　分组后的均值与方差：Mean23.3000Std.Deviation7.02377Variance49.333Skewness1.163\nKurtosis1.302分组后的直方图：4．3某银行为缩短顾客到银行办理业务等待的时间。准备采用两种排队方式进行试验：一种是所有颐客都进入一个等待队列：另—种是顾客在三千业务窗口处列队3排等待。为比较哪种排队方式使顾客等待的时间更短．两种排队方式各随机抽取9名顾客。得到第一种排队方式的平均等待时间为7．2分钟，标准差为1．97分钟。第二种排队方式的等待时间(单位：分钟)如下：5．56．66．76．87．17．37．47．87．8要求：(1)画出第二种排队方式等待时间的茎叶图。第二种排队方式的等待时间(单位：分钟)Stem-and-LeafPlotFrequencyStem&Leaf1.00Extremes(=<5.5)3.006.6783.007.1342.007.88Stemwidth:1.00Eachleaf:1case(s)(2)计算第二种排队时间的平均数和标准差。Mean7Std.Deviation0.Variance0.51\n(3)比较两种排队方式等待时间的离散程度。第二种排队方式的离散程度小。(4)如果让你选择一种排队方式，你会选择哪—种？试说明理由。选择第二种，均值小，离散程度小。4．4某百货公司6月份各天的销售额数据如下：单位：万元257276297252238310240236265278271292261281301274267280291258272284268303273263322249269295要求：(1)计算该百货公司日销售额的平均数和中位数。(2)按定义公式计算四分位数。(3)计算日销售额的标准差。解：Statistics百货公司每天的销售额（万元）NValid30Missing0Mean274.1000Median272.5000Std.Deviation21.17472Percentiles25260.250050272.500075291.25004．5甲乙两个企业生产三种产品的单位成本和总成本资料如下：产品单位成本总成本(元)名称(元)甲企业乙企业ABC152030210030001500325515001500要求：比较两个企业的总平均成本，哪个高，并分析其原因。产品名称单位成本(元)甲企业乙企业总成本(元)产品数总成本(元)产品数A1521001403255217B203000150150075C30150050150050平均成本（元）19.18.调和平均数计算，得到甲的平均成本为19.41；乙的平均成本为18.29。甲的中间成本的产品多，乙的低成本的产品多。\n4．6在某地区抽取120家企业，按利润额进行分组，结果如下：按利润额分组(万元)企业数(个)200~300300~400400~500500~600600以上1930421811合计120要求：(1)计算120家企业利润额的平均数和标准差。(2)计算分布的偏态系数和峰态系数。解：Statistics企业利润组中值Mi（万元）NValid120Missing0Mean426.6667Std.Deviation116.48445Skewness0.208Std.ErrorofSkewness0.221Kurtosis-0.625Std.ErrorofKurtosis0.438\n4．7为研究少年儿童的成长发育状况，某研究所的一位调查人员在某城市抽取100名7～17岁的少年儿童作为样本，另一位调查人员则抽取了1000名7～17岁的少年儿童作为样本。请回答下面的问题，并解释其原因。(1)两位调查人员所得到的样本的平均身高是否相同?如果不同，哪组样本的平均身高较大?(2)两位调查人员所得到的样本的标准差是否相同?如果不同，哪组样本的标准差较大?(3)两位调查人员得到这l100名少年儿童身高的最高者或最低者的机会是否相同?如果不同，哪位调查研究人员的机会较大?解：（1）不一定相同，无法判断哪一个更高，但可以判断，样本量大的更接近于总体平均身高。（2）不一定相同，样本量少的标准差大的可能性大。（3）机会不相同，样本量大的得到最高者和最低者的身高的机会大。4．8一项关于大学生体重状况的研究发现．男生的平均体重为60kg，标准差为5kg；女生的平均体重为50kg，标准差为5kg。请回答下面的问题：(1)是男生的体重差异大还是女生的体重差异大?为什么?女生，因为标准差一样，而均值男生大，所以，离散系数是男生的小，离散程度是男生的小。(2)以磅为单位(1ks＝2．2lb)，求体重的平均数和标准差。都是各乘以2.21，男生的平均体重为60kg×2.21=132.6磅，标准差为5kg×\n2.21=11.05磅；女生的平均体重为50kg×2.21=110.5磅，标准差为5kg×2.21=11.05磅。(3)粗略地估计一下，男生中有百分之几的人体重在55kg一65kg之间?计算标准分数：Z1===-1；Z2===1，根据经验规则，男生大约有68%的人体重在55kg一65kg之间。(4)粗略地估计一下，女生中有百分之几的人体重在40kg～60kg之间?计算标准分数：Z1===-2；Z2===2，根据经验规则，女生大约有95%的人体重在40kg一60kg之间。4．9一家公司在招收职员时，首先要通过两项能力测试。在A项测试中，其平均分数是100分，标准差是15分；在B项测试中，其平均分数是400分，标准差是50分。一位应试者在A项测试中得了115分，在B项测试中得了425分。与平均分数相比，该应试者哪一项测试更为理想?解：应用标准分数来考虑问题，该应试者标准分数高的测试理想。ZA===1；ZB===0.5因此，A项测试结果理想。4．10一条产品生产线平均每天的产量为3700件，标准差为50件。如果某一天的产量低于或高于平均产量，并落人士2个标准差的范围之外，就认为该生产线“失去控制”。下面是一周各天的产量，该生产线哪几天失去了控制?时间周一周二周三周四周五周六周日产量(件)3850367036903720361035903700时间周一周二周三周四周五周六周日产量(件)3850367036903720361035903700日平均产量3700日产量标准差50标准分数Z3-0.6-0.20.4-1.8-2.20标准分数界限-2-2-2-2-2-2-22222222周六超出界限，失去控制。4．11对10名成年人和10名幼儿的身高进行抽样调查，结果如下：成年组166169l72177180170172174168173幼儿组686968707l7372737475要求：(1)如果比较成年组和幼儿组的身高差异，你会采用什么样的统计量?为什么?均值不相等，用离散系数衡量身高差异。(2)比较分析哪一组的身高差异大?\n成年组幼儿组平均172.1平均71.3标准差4.标准差2.离散系数0.离散系数0.幼儿组的身高差异大。4．12一种产品需要人工组装，现有三种可供选择的组装方法。为检验哪种方法更好，随机抽取15个工人，让他们分别用三种方法组装。下面是15个工人分别用三种方法在相同的时间内组装的产品数量：单位：个方法A方法B方法C164167168165170165164168164162163166167166165129130129130131]30129127128128127128128125132125126126127126128127126127127125126116126125要求：(1)你准备采用什么方法来评价组装方法的优劣?(2)如果让你选择一种方法，你会作出怎样的选择?试说明理由。解：对比均值和离散系数的方法，选择均值大，离散程度小的。方法A方法B方法C平均165.6平均128.平均125.标准差2.标准差1.标准差2.离散系数：VA=0.，VB=0.，VC=0.均值A方法最大，同时A的离散系数也最小，因此选择A方法。4．13\n在金融证券领域，一项投资的预期收益率的变化通常用该项投资的风险来衡量。预期收益率的变化越小，投资风险越低；预期收益率的变化越大，投资风险就越高。下面的两个直方图，分别反映了200种商业类股票和200种高科技类股票的收益率分布。在股票市场上，高收益率往往伴随着高风险。但投资于哪类股票，往往与投资者的类型有一定关系。(1)你认为该用什么样的统计量来反映投资的风险?标准差或者离散系数。(2)如果选择风险小的股票进行投资，应该选择商业类股票还是高科技类股票?选择离散系数小的股票，则选择商业股票。(3)如果进行股票投资，你会选择商业类股票还是高科技类股票?考虑高收益，则选择高科技股票；考虑风险，则选择商业股票。\n6.1调节一个装瓶机使其对每个瓶子的灌装量均值为盎司，通过观察这台装瓶机对每个瓶子的灌装量服从标准差盎司的正态分布。随机抽取由这台机器灌装的9个瓶子形成一个样本，并测定每个瓶子的灌装量。试确定样本均值偏离总体均值不超过0.3盎司的概率。解：总体方差知道的情况下，均值的抽样分布服从的正态分布，由正态分布，标准化得到标准正态分布：z=～，因此，样本均值不超过总体均值的概率P为：====2-1，查标准正态分布表得=0.8159因此，=0.63186.2无6.3，，……，表示从标准正态总体中随机抽取的容量，n=6的一个样本，试确定常数b，使得解：由于卡方分布是由标准正态分布的平方和构成的：设Z1，Z2，……，Zn是来自总体N(0,1)的样本，则统计量服从自由度为n的χ2分布，记为χ2～χ2（n）因此，令，则，那么由概率，可知：b=，查概率表得：b=12.596.4在习题6.1中，假定装瓶机对瓶子的灌装量服从方差的标准正态分布。假定我们计划随机抽取10个瓶子组成样本，观测每个瓶子的灌装量，得到10个观测值，用这10个观测值我们可以求出样本方差，确定一个合适的范围使得有较大的概率保证S2落入其中是有用的，试求b1，b2，使得\n解：更加样本方差的抽样分布知识可知，样本统计量：此处，n=10，，所以统计量根据卡方分布的可知：又因为：因此：则：查概率表：=3.325，=19.919，则=0.369，=1.88\n第四章抽样分布与参数估计7.1无7.2某快餐店想要估计每位顾客午餐的平均花费金额。在为期3周的时间里选取49名顾客组成了一个简单随机样本。(1)假定总体标准差为15元，求样本均值的抽样标准误差。=2.143(2)在95％的置信水平下，求边际误差。，由于是大样本抽样，因此样本均值服从正态分布，因此概率度t=因此，=1.96×2.143=4.2(3)如果样本均值为120元，求总体均值的95％的置信区间。置信区间为：==（115.8，124.2）7.3无7.4从总体中抽取一个n=100的简单随机样本,得到=81，s=12。要求：大样本，样本均值服从正态分布：或置信区间为：，==1.2(1)构建的90％的置信区间。==1.645，置信区间为：=（79.03，82.97）(2)构建的95％的置信区间。==1.96，置信区间为：=（78.65，83.35）(3)构建的99％的置信区间。==2.576，置信区间为：=（77.91，84.09）\n7.5无7.6无7.7某大学为了解学生每天上网的时间，在全校7500名学生中采取重复抽样方法随机抽取36人，调查他们每天上网的时间，得到下面的数据(单位：小时)：3.33.16.25.82.34.15.44.53.24.42.05.42.66.41.83.55.72.32.11.91.25.14.34.23.60.81.54.71.41.22.93.52.40.53.62.5求该校大学生平均上网时间的置信区间，置信水平分别为90％，95％和99％。解：（1）样本均值=3.32，样本标准差s=1.61；（2）抽样平均误差：重复抽样：==1.61/6=0.268不重复抽样：===0.268×=0.268×0.998=0.267（3）置信水平下的概率度：=0.9，t===1.645=0.95，t===1.96=0.99，t===2.576（4）边际误差（极限误差）：=0.9，=重复抽样：==1.645×0.268=0.441不重复抽样：==1.645×0.267=0.439=0.95，=重复抽样：==1.96×0.268=0.525不重复抽样：==1.96×0.267=0.523\n=0.99，=重复抽样：==2.576×0.268=0.69不重复抽样：==2.576×0.267=0.688（5）置信区间：=0.9，重复抽样：==（2.88，3.76）不重复抽样：==（2.88，3.76）=0.95，重复抽样：==（2.79，3.85）不重复抽样：==（2.80，3.84）=0.99，重复抽样：==（2.63，4.01）不重复抽样：==（2.63，4.01）7.8无7.9某居民小区为研究职工上班从家里到单位的距离，抽取了由16个人组成的一个随机样本，他们到单位的距离(单位：km)分别是：103148691211751015916132假定总体服从正态分布，求职工上班从家里到单位平均距离的95％的置信区间。解：小样本，总体方差未知，用t统计量均值=9.375，样本标准差s=4.11置信区间：=0.95，n=16，==2.13\n==（7.18，11.57）7.10无7．11某企业生产的袋装食品采用自动打包机包装，每袋标准重量为l00g。现从某天生产的一批产品中按重复抽样随机抽取50包进行检查，测得每包重量(单位：g)如下：每包重量（g）包数96~9898~100100~102102~104104~106233474合计50已知食品包重量服从正态分布，要求：(1)确定该种食品平均重量的95％的置信区间。解：大样本，总体方差未知，用z统计量样本均值=101.4，样本标准差s=1.829置信区间：=0.95，==1.96==（100.89，101.91）(2)如果规定食品重量低于l00g属于不合格，确定该批食品合格率的95％的置信区间。解：总体比率的估计大样本，总体方差未知，用z统计量样本比率=（50-5）/50=0.9置信区间：\n=0.95，==1.96==（0.8168，0.9832）7.12无7．13一家研究机构想估计在网络公司工作的员工每周加班的平均时间，为此随机抽取了18个员工。得到他们每周加班的时间数据如下(单位：小时)：63218171220117902182516152916假定员工每周加班的时间服从正态分布。估计网络公司员工平均每周加班时间的90%的置信区间。解：小样本，总体方差未知，用t统计量均值=13.56，样本标准差s=7.801置信区间：=0.90，n=18，==1.7369==（10.36，16.75）7.14无7．15在一项家电市场调查中．随机抽取了200个居民户，调查他们是否拥有某一品牌的电视机。其中拥有该品牌电视机的家庭占23％。求总体比例的置信区间，置信水平分别为90%和95%。解：总体比率的估计大样本，总体方差未知，用z统计量\n样本比率=0.23置信区间：=0.90，==1.645==（0.1811，0.2789）=0.95，==1.96==（0.1717，0.2883）7.16无7.17无7.18无7.19无7．20顾客到银行办理业务时往往需要等待一段时间，而等待时间的长短与许多因素有关，比如，银行业务员办理业务的速度，顾客等待排队的方式等。为此，某银行准备采取两种排队方式进行试验，第一种排队方式是：所有顾客都进入一个等待队列；第二种排队方式是：顾客在三个业务窗口处列队三排等待。为比较哪种排队方式使顾客等待的时间更短，银行各随机抽取10名顾客，他们在办理业务时所等待的时间(单位：分钟)如下：方式16.56.66.76.87.17.37.47.77.77.7方式24.25.45.86.26.77.77.78.59.310要求：\n(1)构建第一种排队方式等待时间标准差的95％的置信区间。解：估计统计量经计算得样本标准差=3.318置信区间：=0.95，n=10，==19.02，==2.7==（0.1075，0.7574）因此，标准差的置信区间为（0.3279，0.8703）(2)构建第二种排队方式等待时间标准差的95％的置信区间。解：估计统计量经计算得样本标准差=0.2272置信区间：=0.95，n=10，==19.02，==2.7==（1.57，11.06）因此，标准差的置信区间为（1.25，3.33）(3)根据(1)和(2)的结果，你认为哪种排队方式更好?第一种方式好，标准差小！7.21无7.22无7．23下表是由4对观察值组成的随机样本。配对号来自总体A的样本来自总体B的样本120\n2345108765(1)计算A与B各对观察值之差，再利用得出的差值计算和。=1.75，=2.62996(2)设分别为总体A和总体B的均值，构造的95％的置信区间。解：小样本，配对样本，总体方差未知，用t统计量均值=1.75，样本标准差s=2.62996置信区间：=0.95，n=4，==3.182==（-2.43，5.93）7.24无7．25从两个总体中各抽取一个＝250的独立随机样本，来自总体1的样本比例为＝40％，来自总体2的样本比例为＝30％。要求：(1)构造的90％的置信区间。(2)构造的95％的置信区间。解：总体比率差的估计大样本，总体方差未知，用z统计量样本比率p1=0.4，p2=0.3\n置信区间：=0.90，==1.645==（3.02%，16.98%）=0.95，==1.96==（1.68%，18.32%）7.26生产工序的方差是工序质量的一个重要度量。当方差较大时，需要对序进行改进以减小方差。下面是两部机器生产的袋茶重量(单位：g)的数据：机器1机器23.453.223.93.223.283.353.22.983.73.383.193.33.223.753.283.33.23.053.53.383.353.33.293.332.953.453.23.343.353.273.163.483.123.283.163.283.23.183.253.33.343.25要求：构造两个总体方差比/的95％的置信区间。解：统计量：\n置信区间：=0.058，=0.006n1=n2=21=0.95，==2.4645，====0.4058=（4.05，24.6）7．27根据以往的生产数据，某种产品的废品率为2％。如果要求95％的置信区间，若要求边际误差不超过4％，应抽取多大的样本?解：=0.95，==1.96==47.06，取n=48或者50。7．28某超市想要估计每个顾客平均每次购物花费的金额。根据过去的经验，标准差大约为120元，现要求以95％的置信水平估计每个顾客平均购物金额的置信区间，并要求边际误差不超过20元，应抽取多少个顾客作为样本?\n解：，=0.95，==1.96，=138.3，取n=139或者140，或者150。7．29假定两个总体的标准差分别为：，，若要求误差范围不超过5，相应的置信水平为95％，假定，估计两个总体均值之差时所需的样本量为多大?解：n1=n2=，=0.95，==1.96，n1=n2===56.7，取n=58，或者60。7．30假定，边际误差E＝0．05，相应的置信水平为95％，估计两个总体比例之差时所需的样本量为多大?解：n1=n2=，=0.95，==1.96，取p1=p2=0.5，n1=n2===768.3，取n=769，或者780或800。8.1无8．2一种元件，要求其使用寿命不得低于700小时。现从一批这种元件中随机抽取36件，测得其平均寿命为680小时。已知该元件寿命服从正态分布，＝60小时，试在显著性水平0．05下确定这批元件是否合格。解：H0：μ≥700；H1：μ＜700已知：＝680＝60由于n=36＞30，大样本，因此检验统计量：＝＝-2\n当α＝0.05，查表得＝1.645。因为z＜-，故拒绝原假设，接受备择假设，说明这批产品不合格。8.3无8．4糖厂用自动打包机打包，每包标准重量是100千克。每天开工后需要检验一次打包机工作是否正常。某日开工后测得9包重量(单位：千克)如下：99．398．7100．5101．298．399．799．5102．1100．5已知包重服从正态分布，试检验该日打包机工作是否正常(a＝0．05)?解：H0：μ＝100；H1：μ≠100经计算得：＝99.9778S＝1.21221检验统计量：＝＝-0.055当α＝0.05，自由度n－1＝9时，查表得＝2.262。因为＜，样本统计量落在接受区域，故接受原假设，拒绝备择假设，说明打包机工作正常。8．5某种大量生产的袋装食品，按规定不得少于250克。今从一批该食品中任意抽取50袋，发现有6袋低于250克。若规定不符合标准的比例超过5％就不得出厂，问该批食品能否出厂(a＝0．05)?解：解：H0：π≤0.05；H1：π＞0.05已知：p＝6/50=0.12检验统计量：＝＝2.271当α＝0.05，查表得＝1.645。因为＞，样本统计量落在拒绝区域，故拒绝原假设，接受备择假设，说明该批食品不能出厂。8.6无8．7某种电子元件的寿命x(单位：小时)服从正态分布。现测得16只元件的寿命如下：159280101212224379179264222362168250149260485170问是否有理由认为元件的平均寿命显著地大于225小时(a＝0．05)?解：H0：μ≤225；H1：μ＞225经计算知：＝241.5s＝98.726检验统计量：\n＝＝0.669当α＝0.05，自由度n－1＝15时，查表得＝1.753。因为t＜，样本统计量落在接受区域，故接受原假设，拒绝备择假设，说明元件寿命没有显著大于225小时。8.8无8.9无8．10装配一个部件时可以采用不同的方法，所关心的问题是哪一个方法的效率更高。劳动效率可以用平均装配时间反映。现从不同的装配方法中各抽取12件产品，记录各自的装配时间(单位：分钟)如下：甲方法：313429323538343029323126乙方法：262428293029322631293228两总体为正态总体，且方差相同。问两种方法的装配时间有无显著不同(a＝0．05)?解：建立假设H0：μ1－μ2=0H1：μ1－μ2≠0总体正态，小样本抽样，方差未知，方差相等，检验统计量根据样本数据计算，得＝12，=12，＝31.75，＝3.19446，＝28.6667，=2.46183。＝＝8.1326＝2.648α＝0.05时，临界点为＝＝2.074，此题中＞，故拒绝原假设，认为两种方法的装配时间有显著差异。8．11调查了339名50岁以上的人，其中205名吸烟者中有43个患慢性气管炎，在134名不吸烟者中有13人患慢性气管炎。调查数据能否支持“吸烟者容易患慢性气管炎”\n这种观点(a＝0．05)?解：建立假设H0：π1≤π2；H1：π1＞π2p1＝43/205=0.2097n1=205p2＝13/134=0.097n2=134检验统计量＝＝3当α＝0.05，查表得＝1.645。因为＞，拒绝原假设，说明吸烟者容易患慢性气管炎。8．12为了控制贷款规模，某商业银行有个内部要求，平均每项贷款数额不能超过60万元。随着经济的发展，贷款规模有增大的趋势。银行经理想了解在同样项目条件下，贷款的平均规模是否明显地超过60万元，故一个n=144的随机样本被抽出，测得=68．1万元，s=45。用a＝0．01的显著性水平，采用p值进行检验。解：H0：μ≤60；H1：μ＞60已知：＝68.1s=45由于n=144＞30，大样本，因此检验统计量：＝＝2.16由于＞μ，因此P值=P（z≥2.16）=1-，查表的=0.9846，P值=0.0154由于P＞α＝0.01，故不能拒绝原假设，说明贷款的平均规模没有明显地超过60万元。8．13有一种理论认为服用阿司匹林有助于减少心脏病的发生，为了进行验证，研究人员把自愿参与实验的22000人随机平均分成两组，一组人员每星期服用三次阿司匹林(样本1)，另一组人员在相同的时间服用安慰剂(样本2)持续3年之后进行检测，样本1中有104人患心脏病，样本2中有189人患心脏病。以a＝0．05的显著性水平检验服用阿司匹林是否可以降低心脏病发生率。解：建立假设H0：π1≥π2；H1：π1＜π2p1＝104/11000=0.00945n1=11000p2＝189/11000=0.01718n2=11000检验统计量\n＝＝-5当α＝0.05，查表得＝1.645。因为＜-，拒绝原假设，说明用阿司匹林可以降低心脏病发生率。8.14无8．15有人说在大学中男生的学习成绩比女生的学习成绩好。现从一个学校中随机抽取了25名男生和16名女生，对他们进行了同样题目的测试。测试结果表明，男生的平均成绩为82分，方差为56分，女生的平均成绩为78分，方差为49分。假设显著性水平α=0．02，从上述数据中能得到什么结论?解：首先进行方差是否相等的检验：建立假设H0：＝；H1：≠n1=25，=56，n2=16，=49＝＝1.143当α＝0.02时，＝3.294，＝0.346。由于＜F＜，检验统计量的值落在接受域中，所以接受原假设，说明总体方差无显著差异。检验均值差：建立假设H0：μ1－μ2≤0H1：μ1－μ2＞0总体正态，小样本抽样，方差未知，方差相等，检验统计量根据样本数据计算，得＝25，=16，＝82，=56，＝78，=49＝53.308＝1.711\nα＝0.02时，临界点为＝＝2.125，t＜，故不能拒绝原假设，不能认为大学中男生的学习成绩比女生的学习成绩好。\n10.1无10.2无10．3一家牛奶公司有4台机器装填牛奶，每桶的容量为4L。下面是从4台机器中抽取的样本数据：机器l机器2机器3机器44.053.993.974.004.014.023.984.024.024.013.973.994.043.993.954.0l4.004.004.00取显著性水平a＝0.01，检验4台机器的装填量是否相同?解：ANOVA每桶容量（L）平方和df均方F显著性组间0.00730.0028.7210.001组内0.004150.000　　总数0.01118　　　不相同。10.4无10.5无10.6无10．7某企业准备用三种方法组装一种新的产品，为确定哪种方法每小时生产的产品数量最多，随机抽取了30名工人，并指定每个人使用其中的一种方法。通过对每个工人生产的产品数进行方差分析得到下面的结果；方差分析表差异源SSdfMSFP-valueFcrit组间42022101.0.3.组内383627142.———总计425629————要求：(1)完成上面的方差分析表。(2)若显著性水平a=0.05，检验三种方法组装的产品数量之间是否有显著差异?解：（2）P=0.025＞a=0.05，没有显著差异。10.8无10.9有5种不同品种的种子和4种不同的施肥方案，在20块同样面积的土地上，分别采用5种种子和4种施肥方案搭配进行试验，取得的收获量数据如下表：\n品种施肥方案1234112．09．510．49．7213．711．512．49．6314．312．311．411．1414．214．012．512．0513.014．013．111.4检验种子的不同品种对收获量的影响是否有显著差异?不同的施肥方案对收获量的影响是否有显著差异(a=0.05)?解：这线图：__似乎交互作用不明显：（1）考虑无交互作用下的方差分析：主体间效应的检验因变量:收获量源III型平方和df均方FSig.校正模型37.249(a)75.3218.0820.001截距2,930.62112,930.6214,451.0120.000Fertilization_Methods18.18236.0619.2050.002Variety19.06744.7677.2400.003误差7.901120.658　　总计2,975.77020　　　校正的总计45.15019　　　a.R方=.825（调整R方=.723）结果表明施肥方法和品种都对收获量有显著影响。（2）考虑有交互作用下的方差分析：\n主体间效应的检验因变量:收获量源III型平方和df均方FSig.校正模型45.150(a)192.376..截距2,930.62112,930.621..Fertilization_Methods18.18236.061..Variety19.06744.767..Fertilization_Methods*Variety7.901120.658..误差0.0000.　　总计2,975.77020　　　校正的总计45.15019　　　a.R方=1.000（调整R方=.）由于观测数太少，得不到结果！10.10无10．11一家超市连锁店进行一项研究，确定超市所在的位置和竞争者的数量对销售额是否有显著影响。下面是获得的月销售额数据(单位：万元)。超市位置竞争者数量0123个以h位于市内居民小区413859473031484045395139位于写字楼252944433135484222305053位于郊区187229242917282733252632取显著性水平a=0．01，检验：(1)竞争者的数量对销售额是否有显著影响?(2)超市的位置对销售额是否有显著影响?(3)竞争者的数量和超市的位置对销售额是否有交互影响?解：画折线图：\n交互作用不十分明显。（1）进行无交互方差分析：主体间效应的检验因变量:月销售额（万元）源III型平方和df均方FSig.校正模型2814.556(a)5562.91115.2050.000截距44,802.778144,802.7781,210.1590.000Location_SuperMaket1,736.2222868.11123.4480.000Amount_competitors1,078.3333359.4449.7090.000误差1,110.6673037.022　　总计48,728.00036　　　校正的总计3,925.22235　　　a.R方=.717（调整R方=.670）看到超市位置有显著影响，而竞争者数量没有显著影响，且影响强度仅为0.327，因此考虑是否存在交互作用。（2）有交互方差分析：看到超市位置有显著影响，而竞争者数量和交互作用均无显著影响。主体间效应的检验因变量:月销售额（万元）源III型平方和df均方FSig.校正模型3317.889(a)11301.62611.9190.000\n截距44,802.778144,802.7781,770.4720.000Location_SuperMaket1,736.2222868.11134.3050.000Amount_competitors1,078.3333359.44414.2040.000Location_SuperMaket*Amount_competitors503.333683.8893.3150.016误差607.3332425.306　　总计48,728.00036　　　校正的总计3,925.22235　　　a.R方=.845（调整R方=.774）10.12无11.1无11.2无11.3无11.4无11.5一家物流公司的管理人员想研究货物的运输距离和运输时间的关系，为此，他抽出了公司最近10个卡车运货记录的随机样本，得到运送距离(单位：km)和运送时间(单位：天)的数据如下：运送距离x825215107055048092013503256701215运送时间y3.51.04.02.01.03.04.51.53.05.0要求：(1)绘制运送距离和运送时间的散点图，判断二者之间的关系形态：(2)计算线性相关系数，说明两个变量之间的关系强度。(3)利用最小二乘法求出估计的回归方程，并解释回归系数的实际意义。解：（1）\n__可能存在线性关系。（2）相关性x运送距离（km）y运送时间（天）x运送距离（km）Pearson相关性1.949(**)显著性（双侧）　0.000N1010y运送时间（天）Pearson相关性.949(**)1显著性（双侧）0.000　N1010**.在.01水平（双侧）上显著相关。有很强的线性关系。（3）系数(a)模型非标准化系数标准化系数t显著性B标准误Beta1（常量）0.1180.355　0.3330.748x运送距离（km）0.0040.0000.9498.5090.000a.因变量:y运送时间（天）回归系数的含义：每公里增加0.004天。11.6下面是7个地区2000年的人均国内生产总值（GDP）和人均消费水平的统计数据：\n地区人均GDP(元)人均消费水平(元)北京辽宁上海江西河南贵州陕西224601122634547485154442662454973264490115462396220816082035要求：(1)人均GDP作自变量，人均消费水平作因变量，绘制散点图，并说明二者之间的关系形态。(2)计算两个变量之间的线性相关系数，说明两个变量之间的关系强度。(3)利用最小二乘法求出估计的回归方程，并解释回归系数的实际意义。(4)计算判定系数，并解释其意义。(5)检验回归方程线性关系的显著性(a=0.05)。(6)如果某地区的人均GDP为5000元，预测其人均消费水平。(7)求人均GDP为5000元时，人均消费水平95％的置信区间和预测区间。解：（1）__可能存在线性关系。（2）相关系数：相关性人均GDP（元）人均消费水平（元）\n人均GDP（元）Pearson相关性1.998(**)显著性（双侧）　0.000N77人均消费水平（元）Pearson相关性.998(**)1显著性（双侧）0.000　N77**.在.01水平（双侧）上显著相关。有很强的线性关系。（3）回归方程：系数(a)模型非标准化系数标准化系数t显著性B标准误Beta1（常量）734.693139.540　5.2650.003人均GDP（元）0.3090.0080.99836.4920.000a.因变量:人均消费水平（元）回归系数的含义：人均GDP没增加1元，人均消费增加0.309元。（4）模型摘要模型RR方调整的R方估计的标准差1.998(a)0.9960.996247.303a.预测变量:(常量),人均GDP（元）。人均GDP对人均消费的影响达到99.6%。（5）F检验：ANOVA(b)模型平方和df均方F显著性1回归81,444,968.680181,444,968.6801,331.692.000(a)残差305,795.034561,159.007　　合计81,750,763.7146　　　a.预测变量:(常量),人均GDP（元）。b.因变量:人均消费水平（元）回归系数的检验：t检验系数(a)模型非标准化系数标准化系数t显著性B标准误Beta1（常量）734.693139.540　5.2650.003人均GDP（元）0.3090.0080.99836.4920.000a.因变量:人均消费水平（元）（6）某地区的人均GDP为5000元，预测其人均消费水平为2278.10657元。（7）人均GDP为5000元时，人均消费水平95％的置信区间为[1990.74915，2565.46399\n]，预测区间为[1580.46315，2975.74999]。11.7无11.8无11.9某汽车生产商欲了解广告费用(x)对销售量(y)的影响，收集了过去12年的有关数据。通过计算得到下面的有关结果：方差分析表变差来源dfSSMSFSignificanceF回归1.6.6399.2.17E—09残差1040158.074015.807——总计11.67———参数估计表Coefficients标准误差tStatP—valueIntercept363.689162.455295.0.XVariable11.0.19.977492.17E—09要求：(1)完成上面的方差分析表。(2)汽车销售量的变差中有多少是由于广告费用的变动引起的?(3)销售量与广告费用之间的相关系数是多少?(4)写出估计的回归方程并解释回归系数的实际意义。(5)检验线性关系的显著性(a＝0.05)。解：（2）R2=0.9756，汽车销售量的变差中有97.56%是由于广告费用的变动引起的。（3）r=0.9877。（4）回归系数的意义：广告费用每增加一个单位，汽车销量就增加1.42个单位。（5）回归系数的检验：p=2.17E—09＜α，回归系数不等于0，显著。回归直线的检验：p=2.17E—09＜α，回归直线显著。11.10无11.11从20的样本中得到的有关回归结果是：SSR=60，SSE=40。要检验x与y之间的线性关系是否显著，即检验假设：。(1)线性关系检验的统计量F值是多少?(2)给定显著性水平a＝0.05，Fa是多少?(3)是拒绝原假设还是不拒绝原假设?(4)假定x与y之间是负相关，计算相关系数r。\n(5)检验x与y之间的线性关系是否显著?解：（1）SSR的自由度为k=1；SSE的自由度为n-k-1=18；因此：F===27（2）==4.41（3）拒绝原假设，线性关系显著。（4）r===0.7746，由于是负相关，因此r=-0.7746（5）从F检验看线性关系显著。11.12无11.13无11.14无11.15随机抽取7家超市，得到其广告费支出和销售额数据如下：超市广告费支出(万元)销售额(万元)ABCDEFGl24610142019324440525354要求：(1)用广告费支出作自变量x，销售额作因变量y，求出估计的回归方程。(2)检验广告费支出与销售额之间的线性关系是否显著(a＝0.05)。(3)绘制关于x的残差图，你觉得关于误差项的假定被满足了吗?(4)你是选用这个模型，还是另寻找一个更好的模型?解：（1）系数(a)模型非标准化系数标准化系数t显著性B标准误Beta1（常量）29.3994.807　6.1160.002广告费支出（万元）1.5470.4630.8313.3390.021a.因变量:销售额（万元）（2）回归直线的F检验：ANOVA(b)\n模型平方和df均方F显著性1回归691.7231691.72311.147.021(a)残差310.277562.055　　合计1,002.0006　　　a.预测变量:(常量),广告费支出（万元）。b.因变量:销售额（万元）显著。回归系数的t检验：系数(a)模型非标准化系数标准化系数t显著性B标准误Beta1（常量）29.3994.807　6.1160.002广告费支出（万元）1.5470.4630.8313.3390.021a.因变量:销售额（万元）显著。（3）未标准化残差图：__标准化残差图：\n学生氏标准化残差图：\n看到残差不全相等。（4）应考虑其他模型。可考虑对数曲线模型：y=b0+b1ln(x)=22.471+11.576ln(x)。\n12.1无12.2根据下面Excel输出的回归结果，说明模型中涉及多少个自变量、少个观察值？写出回归方程，并根据F，se，R2及调整的的值对模型进行讨论。SUMMARYOUTPUT回归统计MultipleRRSquareAdjustedRSquare标准误差观测值0.0.0.109.15方差分析dfSSMSFSignificanceF回归3.8018.60068.0.残差11.198211974.84总计14Coefficients标准误差tStatP-valueInterceptXVariable1XVariable2XVariable3657.05345.-0.-3.167.1.0.1.3.3.-1.-2.0.0.0.0.解：自变量3个，观察值15个。回归方程：=657.0534+5.X1-0.X2-3.X3拟合优度：判定系数R2=0.70965，调整的=0.，说明三个自变量对因变量的影响的比例占到63%。估计的标准误差=109.，说明随即变动程度为109.回归方程的检验：F检验的P=0.，在显著性为5%的情况下，整个回归方程线性关系显著。回归系数的检验：的t检验的P=0.，在显著性为5%的情况下，y与X1线性关系显著。的t检验的P=0.，在显著性为5%的情况下，y与X2线性关系不显著。的t检验的P=0.，在显著性为5%的情况下，y与X3线性关系显著。因此，可以考虑采用逐步回归去除X2，从新构建线性回归模型。12.3根据两个自变量得到的多元回归方程为，并且已知n＝10，SST＝6724.125，SSR＝6216.375，，＝0.0567。要求：\n(1)在a=0.05的显著性水平下，与y的线性关系是否显著?(2)在a＝0.05的显著性水平下，是否显著?(3)在a＝0.05的显著性水平下，是否显著?解（1）回归方程的显著性检验：假设：H0：==0H1：，不全等于0SSE=SST-SSR=6724.125-6216.375=507.75F===42.85=4.74，F>，认为线性关系显著。（2）回归系数的显著性检验：假设：H0：=0H1：≠0t===24.72=2.36，>，认为y与x1线性关系显著。（3）回归系数的显著性检验：假设：H0：=0H1：≠0t===83.6=2.36，>，认为y与x2线性关系显著。12.4一家电器销售公司的管理人员认为，每月的销售额是广告费用的函数，并想通过广告费用对月销售额作出估计。下面是近8个月的销售额与广告费用数据：月销售收入y(万元)电视广告费用工：x1(万元)报纸广告费用x2(万元)\n96909592959494945．02．04．02．53．03．52．53．01.52．01．52.53．32．34．22．5要求：(1)用电视广告费用作自变量，月销售额作因变量，建立估计的回归方程。(2)用电视广告费用和报纸广告费用作自变量，月销售额作因变量，建立估计的回归方程。(3)上述(1)和(2)所建立的估计方程，电视广告费用的系数是否相同?对其回归系数分别进行解释。(4)根据问题(2)所建立的估计方程，在销售收入的总变差中，被估计的回归方程所解释的比例是多少?(5)根据问题(2)所建立的估计方程，检验回归系数是否显著(a=0.05)。解：（1）回归方程为：（2）回归方程为：（3）不相同，（1）中表明电视广告费用增加1万元，月销售额增加1.6万元；（2）中表明，在报纸广告费用不变的情况下，电视广告费用增加1万元，月销售额增加2.29万元。（4）判定系数R2=0.919，调整的=0.8866，比例为88.66%。（5）回归系数的显著性检验：　Coefficients标准误差tStatP-valueLower95%Upper95%下限95.0%上限95.0%Intercept83.230091.52.882484.57E-0879.1843387.2758579.1843387.27585电视广告费用工：x1(万元)2.0.7.0.1.3.1.3.报纸广告费用x2(万元)1.0.4.0.0.2.0.2.假设：H0：=0H1：≠0t===7.53=2.57，>，认为y与x1线性关系显著。（3）回归系数的显著性检验：假设：H0：=0H1：≠0\nt===4.05=2.57，>，认为y与x2线性关系显著。12.5某农场通过试验取得早稻收获量与春季降雨量和春季温度的数据如下：收获量y(kg／hm2)降雨量x1(mm)温度x2(℃)2250345045006750720075008250253345105110115120681013141617要求：(1)试确定早稻收获量对春季降雨量和春季温度的二元线性回归方程。(2)解释回归系数的实际意义。(3)根据你的判断，模型中是否存在多重共线性?解：（1）回归方程为：（2）在温度不变的情况下，降雨量每增加1mm，收获量增加22.386kg／hm2，在降雨量不变的情况下，降雨量每增加1度，收获量增加327.672kg／hm2。（3）与的相关系数=0.965，存在多重共线性。12.6无12.7无12.7无12.9下面是随机抽取的15家大型商场销售的同类产品的有关数据(单位：元)。企业编号销售价格y购进价格x1销售费用x2\nl23456789101112131415l238l266l200119311061303131311441286l084l120115610831263124696689444066479185280490577l51150585l659490696223257387310339283302214304326339235276390316要求：(1)计算y与x1、y与x2之间的相关系数，是否有证据表明销售价格与购进价格、销售价格与销售费用之间存在线性关系?(2)根据上述结果，你认为用购进价格和销售费用来预测销售价格是否有用?(3)用Excel进行回归，并检验模型的线性关系是否显著(a＝0.05)。(4)解释判定系数R2，所得结论与问题(2)中是否一致?(5)计算x1与x2之间的相关系数，所得结果意味着什么?(6)模型中是否存在多重共线性?你对模型有何建议?解：（1）y与x1的相关系数=0.309，y与x2之间的相关系数=0.0012。对相关性进行检验：相关性销售价格购进价格销售费用销售价格Pearson相关性10.3090.001显著性（双侧）　0.2630.997N151515购进价格Pearson相关性0.3091-.853(**)显著性（双侧）0.263　0.000N151515销售费用Pearson相关性0.001-.853(**)1显著性（双侧）0.9970.000　N151515**.在.01水平（双侧）上显著相关。可以看到，两个相关系数的P值都比较的，总体上线性关系也不现状，因此没有明显的线性相关关系。（2）意义不大。\n（3）回归统计MultipleR0.RSquare0.35246AdjustedRSquare0.标准误差69.75121观测值15方差分析　dfSSMSFSignificanceF回归分析231778.153915889.083.0.残差1258382.77944865.232总计1490160.9333　　　　Coefficients标准误差tStatP-valueLower95%Upper95%下限95.0%上限95.0%Intercept375.6018339.1.106630.-363.911115.114-363.911115.114购进价格x10.0.2.0.02520.0.0.0.销售费用x21.0.2.0.0.2.0.2.从检验结果看，整个方程在5%下，不显著；而回归系数在5%下，均显著，说明回归方程没有多大意义，并且自变量间存在线性相关关系。（4）从R2看，调整后的R2=24.4%，说明自变量对因变量影响不大，反映情况基本一致。（5）方程不显著，而回归系数显著，说明可能存在多重共线性。（6）存在多重共线性，模型不适宜采用线性模型。12.11一家货物运输公司想研究运输费用与货物类型的关系，并建立运输费用与货物类型的回归模型，以此对运输费用作出预测。该运输公司所运输的货物分为两种类型：易碎品和非易碎品。下表给出了15个路程大致相同，而货物类型不同的运输费用数据。每件产品的运输费用y(元)货物类型x1\n17．211．112．010．913．86．510．011．57．08．52．1l。33．47．52．0易碎品易碎品易碎品易碎品易碎品易碎品易碎品易碎品非易碎品非易碎品非易碎品非易碎品非易碎品非易碎品非易碎品111l1l110000000要求：(1)写出运输费用与货物类型之间的线性方程。(2)对模型中的回归系数进行解释。(3)检验模型的线性关系是否显著(a＝0.05)。解：　dfSSMSFSignificanceF回归分析1187.2519187.251920.22290.残差13120.37219.总计14307.624　　　　Coefficients标准误差tStatP-valueLower95%Upper95%下限95.0%上限95.0%Intercept4.1.3.0.2.7.2.7.x17.1.4.0.3.10.484433.10.48443（1）回归方程为：（2）非易碎品的平均运费为4.54元，易碎品的平均运费为11.62元，易碎品与非易碎品的平均运费差为7.08元。（3）回归方程的显著性检验：假设：H0：=0H1：不等于0SSR=187.25195，SSE=120.3721，F===20.22\nP=0.<0.05，或者=4.67，F>，认为线性关系显著。或者，回归系数的显著性检验：假设：H0：=0H1：≠0t===4.5P=0.<0.05，或者==2.16，>，认为y与x线性关系显著。12.12为分析某行业中的薪水有无性别歧视，从该行业中随机抽取15名员工，有关数据如下：月薪y(元)工龄x1性别(1=男，0＝女)x2l548l6291011l229l7461528l0181190l551985l6101432121599015853．23．82．73．43．64．13．83．43．33．23．52．93．32．83．5ll00l100l0ll00l要求：用Excel进行回归，并对结果进行分析。解：回归统计MultipleR0.RSquare0.AdjustedRSquare0.标准误差96.79158观测值15方差分析　dfSSMSFSignificanceF回归分析2.4.248.539141.77E-06\n残差12.39368.61总计14　　　　Coefficients标准误差tStatP-valueLower95%Upper95%下限95.0%上限95.0%Intercept732.0606235.58443.0.218.76641245.355218.76641245.355工龄x1111.220272.083421.0.-45.8361268.2765-45.8361268.2765性别(1=男，0＝女)x2458.684153.45858.580191.82E-06342.208575.1601342.208575.1601拟合优度良好，方程线性显著，工龄线性不显著，性别线性显著。13.1下表是1981年—1999年国家财政用于农业的支出额数据年份支出额（亿元）年份支出额（亿元）1981110.211991347.571982120.491992376.021983132.871993440.451984141.291994532.981985153.621995574.931986184.21996700.431987195.721997766.391988214.0719981154.761989265.9419991085.761990307.84　　（1）绘制时间序列图描述其形态。（2）计算年平均增长率。（3）根据年平均增长率预测2000年的支出额。详细答案：（1）时间序列图如下：\n　　从时间序列图可以看出，国家财政用于农业的支出额大体上呈指数上升趋势。（2）年平均增长率为：。（3）。13.2下表是1981年—2000年我国油彩油菜籽单位面积产量数据（单位：kg/hm2）年份单位面积产量年份单位面积产量19811451199112151982137219921281198311681993130919841232199412961985124519951416198612001996136719871260199714791988102019981272\n19891095199914691990126020001519（1）绘制时间序列图描述其形态。（2）用5期移动平均法预测2001年的单位面积产量。（3）采用指数平滑法，分别用平滑系数a=0.3和a=0.5预测2001年的单位面积产量，分析预测误差，说明用哪一个平滑系数预测更合适？详细答案：（1）时间序列图如下：（2）2001年的预测值为：|（3）由Excel输出的指数平滑预测值如下表：年份单位面积产量指数平滑预测a=0.3误差平方指数平滑预测a=0.5误差平方19811451198213721451.06241.01451.06241.0198311681427.367236.51411.559292.3198412321349.513808.61289.83335.1198512451314.34796.51260.9252.0\n198612001293.58738.51252.92802.4198712601265.429.51226.51124.3198810201263.859441.01243.249833.6198910951190.79151.51131.61340.8199012601162.09611.01113.321518.4199112151191.4558.11186.7803.5199212811198.56812.41200.86427.7199313091223.27357.61240.94635.8199412961249.02213.11275.0442.8199514161263.123387.71285.517035.9199613671308.93369.91350.7264.4199714791326.423297.71358.914431.3199812721372.210031.01418.921589.8199914691342.116101.51345.515260.3200015191380.219272.11407.212491.7合计——.2—.02001年a=0.3时的预测值为：a=0.5时的预测值为：比较误差平方可知，a=0.5更合适。13.3下面是一家旅馆过去18个月的营业额数据\n月份营业额（万元）月份营业额（万元）129510473228311470332212481435513449528614544637915601738116587843117644942418660（1）用3期移动平均法预测第19个月的营业额。（2）采用指数平滑法，分别用平滑系数a=0.3、a=0.4和a=0.5预测各月的营业额，分析预测误差，说明用哪一个平滑系数预测更合适？（3）建立一个趋势方程预测各月的营业额，计算出估计标准误差。详细答案：（1）第19个月的3期移动平均预测值为：（2）月份营业额预测a=0.3误差平方预测a=0.4误差平方预测a=0.5误差平方1295　　　　　　2283295.0144.0295.0144.0295.0144.03322291.4936.4290.21011.2289.01089.0\n4355300.62961.5302.92712.3305.52450.35286316.9955.2323.81425.2330.31958.16379307.65093.1308.74949.0308.15023.37381329.02699.4336.81954.5343.61401.68431344.67459.6354.55856.2362.34722.39424370.52857.8385.11514.4396.6748.510473386.67468.6400.75234.4410.33928.711470412.53305.6429.61632.9441.7803.112481429.82626.2445.81242.3455.8633.513449445.115.0459.9117.8468.4376.914544446.39547.4455.57830.2458.77274.815601475.615724.5490.912120.5501.49929.416587513.25443.2534.92709.8551.21283.317644535.411803.7555.87785.2569.15611.718660567.98473.4591.14752.7606.52857.5合计——87514.7—62992.5—50236由Excel输出的指数平滑预测值如下表：a=0.3时的预测值：，误差均方＝87514.7。a=0.4时的预测值：，误差均方＝62992.5.。a=0.5时的预测值：\n，误差均方＝50236。比较各误差平方可知，a=0.5更合适。（3）根据最小二乘法，利用Excel输出的回归结果如下：回归统计　　　　　MultipleR0.9673　　　　　RSquare0.9356　　　　　AdjustedRSquare0.9316　　　　　标准误差31.6628　　　　　观测值18　　　　　　　　　　　　方差分析　　　　　　　dfSSMSFSignificanceF　回归分析1.5.5232.39445.99E-11　残差1616040.491002.53　　　总计17.9　　　　　　　　　　　　Coefficients标准误差tStatP-valueLower95%Upper95%Intercept239.7320315.5705515.39655.16E-11206.7239272.7401XVariable121.1.15.244495.99E-1118.8793624.97822。估计标准误差。13.4下表是1981年—2000年我国财政用于文教、科技、卫生事业费指出额数据\n年份支出（万元）年份支出（万元）1981171.361991708.001982196.961992792.961983223.541993957.771984263.1719941278.181985316.7019951467.061986379.9319961704.251987402.7519971903.591988486.1019982154.381989553.3319992408.061990617.2920002736.88（1）绘制时间序列图描述其趋势。（2）选择一条适合的趋势线拟合数据，并根据趋势线预测2001年的支出额。详细答案：（1）趋势图如下：\n（2）从趋势图可以看出，我国财政用于文教、科技、卫生事业费指出额呈现指数增长趋势，因此，选择指数曲线。经线性变换后，利用Excel输出的回归结果如下：回归统计　　　　　MultipleR0.　　　　　RSquare0.　　　　　AdjustedRSquare0.　　　　　标准误差0.　　　　　观测值20　　　　　　　　　　　　方差分析　　　　　　　　dfSSMSFSignificanceF　回归分析12.2.5694.8855.68E-24　残差180.0.　　　总计192.　　　　　　　　　　　　　　　　Coefficients标准误差tStatP-valueLower95%Upper95%Intercept2.0.210.52695.55E-322.2.XVariable10.0.75.464465.68E-240.0.，；，。所以，指数曲线方程为：。2001年的预测值为：。\n13.5我国1964年～1999年的纱产量数据如下（单位：万吨）：年份纱产量年份纱产量年份纱产量196497.01976196.01988465.71965130.01977223.01989476.71966156.51978238.21990462.61967135.21979263.51991460.81968137.71980292.61992501.81969180.51981317.01993501.51970205.21982335.41994489.51971190.01983327.01995542.31972188.61984321.91996512.21973196.71985353.51997559.81974180.31986397.81998542.01975210.81987436.81999567.0（1）绘制时间序列图描述其趋势。（2）选择一条适合的趋势线拟合数据，并根据趋势线预测2000年的产量。详细答案：（1）趋势图如下：\n（2）从图中可以看出，纱产量具有明显的线性趋势。用Excel求得的线性趋势方程为：2000年预测值为：=585.65（万吨）。13.6对下面的数据分别拟合线性趋势线、二阶曲线和阶次曲线。并对结果进行比较。时间t观测值Y时间t观测值Y137219360237020357337421356437522352537723348637724353737425356837226356\n9373273561037228359113692936012367303571336731357143653235515363333561635934363173583536518359　　详细答案：在求二阶曲线和三阶曲线时，首先将其线性化，然后用最小二乘法按线性回归进行求解。用Excel求得的趋势直线、二阶曲线和三阶曲线的系数如下：直线二阶曲线三阶曲线Intercept374.1613Intercept381.6442Intercept372.5617XVariable1-0.6137XVariable1-1.8272XVariable11.0030　　XVariable20.0337XVariable2-0.1601　　　　XVariable30.0036各趋势方程为：线性趋势：二阶曲线：\n三阶曲线：。根据趋势方程求得的预测值和预测误差如下表：时间t观测值Y直线二阶曲线三阶曲线预测误差平方预测误差平方预测误差平方1372373.52.4379.961.6373.42.02370372.98.6378.166.0374.015.63374372.32.8376.56.1374.20.14375371.710.8374.90.0374.20.65377371.134.9373.413.3374.08.96377370.542.5371.926.1373.611.67374369.917.1370.512.2373.01.18372369.37.6369.27.9372.20.09373368.619.0367.925.7371.23.110372368.015.8366.727.6370.23.311369367.42.5365.611.4369.00.012367366.80.0364.65.9367.70.613367366.20.7363.611.6366.40.314365365.60.3362.75.4365.10.015363365.03.8361.81.4363.70.516359364.328.5361.04.2362.311.117358363.732.8360.35.4361.08.918359363.116.9359.70.5359.70.519360362.56.3359.10.8358.42.4\n20357361.923.9358.62.5357.30.121356361.327.8358.14.6356.30.122352360.775.0357.833.2355.411.323348360.0145.1357.589.3354.643.724353359.441.4357.217.7354.01.125356358.87.9357.01.1353.75.526356358.24.9356.90.9353.56.327356357.62.5356.90.8353.65.928359357.04.1356.94.4353.925.829360356.413.2357.09.0354.529.830357355.71.6357.20.0355.52.331357355.13.5357.40.2356.70.132355354.50.2357.77.2358.311.033356353.94.4358.14.2360.318.434363353.394.2358.520.4362.70.135365352.7151.8359.036.2365.40.2合计——854.9—524.7—232.1不同趋势线预测的标准误差如下：直线：二阶曲线：\n三阶曲线：比较各预测误差可知，直线的误差最大，三阶曲线的误差最小。从不同趋势方程的预测图也可以看出，三阶曲线与原序列的拟合最好。13.7下表是1981—2000年我国的原煤产量数据年份原煤产量（亿吨）年份原煤产量（亿吨）19816.22199110.8719826.66199211.1619837.15199311.5019847.89199412.4019858.72199513.6119868.94199613.9719879.28199713.7319889.80199812.50\n198910.54199910.45199010.8020009.98（1）绘制时间序列图描述其趋势。（2）选择一条适合的趋势线拟合数据，并根据趋势线预测2001年的产量。详细答案：（1）原煤产量趋势图如下：从趋势图可以看出，拟合二阶曲线比较合适。（2）用Excel求得的二阶曲线趋势方程为：2001年的预测值为：。13.8一家贸易公司主要经营产品的外销业务，为了合理地组织货源，需要了解外销订单的变化状况。下表是1997—2001年各月份的外销定单金额（单位：万元）。年/月19971998199920002001154.349.156.764.461.1246.650.452.054.569.4\n362.659.361.768.076.5458.258.561.471.971.6557.460.062.469.474.6656.655.663.667.769.9756.158.063.268.071.4852.955.863.966.372.7954.655.863.267.869.91051.359.863.471.574.21154.859.464.470.572.71252.155.563.869.472.5（1）根据各年的月份数据绘制趋势图，说明该时间序列的特点。（2）要寻找各月份的预测值，你认为应该采取什么方法？（3）选择你认为合适的方法预测2002年1月份的外销订单金额。详细答案：（1）趋势图如下：从趋势图可以看出，每一年的各月份数据没有趋势存在，但从1997—2001年的变化看，订单金额存在一定的线性趋势。\n（2）由于是预测各月份的订单金额，因此采用移动平均法或指数平滑法比较合适。（3）用Excel采用12项移动平均法预测的结果为：。用Excel采用指数平滑法（a=0.4）预测的预测结果为：。13.91993—2000年我国社会消费品零售总额数据如下（单位：亿元）月/年199319941995199619971998199920001977.51192.21602.21909.12288.52549.52662.12774.72892.51162.71491.51911.22213.52306.42538.42805.03942.31167.51533.31860.12130.92279.72403.12627.04941.31170.41548.71854.82100.52252.72356.82572.05962.21213.71585.41898.32108.22265.22364.02637.061005.71281.11639.71966.02164.72326.02428.82645.07963.81251.51623.61888.72102.52286.12380.32597.08959.81286.01637.11916.42104.42314.62410.92636.091023.31396.21756.02083.52239.62443.12604.32854.0101051.11444.11818.02148.32348.02536.02743.93029.0111102.01553.81935.22290.12454.92652.22781.53108.0121415.51932.22389.52848.62881.73131.43405.73680.0（1）绘制时间序列线图，说明该序列的特点。（2）利用分解预测法预测2001年各月份的社会消费品零售总额。详细答案：（1）趋势图如下：\n从趋势图可以看出，我国社会消费品零售总额的变具有明显的季节变动和趋势。（2）利用分解法预测的结果如下：2001年/月时间编号季节指数回归预测值最终预测值1971.04393056.303190.482980.99393077.503058.873990.95933098.712972.4841000.93983119.922931.9951010.94393141.132964.8861020.95893162.333032.3071030.92873183.542956.4381040.92613204.752967.8691050.98143225.963166.05101061.00753247.163271.51111071.04723268.373422.77121081.26943289.584175.95\n13.101995年～2000年北京市月平均气温数据如下（单位：）：月/年1995199619971998199920001-0.7-2.2-3.8-3.9-1.6-6.422.1-0.41.32.42.2-1.537.76.28.77.64.88.1414.714.314.515.014.414.6519.821.620.019.919.520.4624.325.424.623.625.426.7725.925.528.226.528.129.6825.423.926.625.125.625.7919.020.718.622.220.921.81014.512.814.014.813.012.6117.74.25.44.05.93.012-0.40.9-1.50.1-0.6-0.6（1）绘制年度折叠时间序列图，判断时间序列的类型。（2）用季节性多元回归模型预测2001年各月份的平均气温。详细答案：（1）年度折叠时间序列图如下：\n从年度折叠时间序列图可以看出，北京市月平均气温具有明显的季节变动。由于折线图中有交叉，表明该序列不存在趋势。（2）季节性多元回归模型为：设月份为。则季节性多元回归模型为：虚拟变量为：，，……，。由Excel输出的回归结果如下：系数b0-0.2233b1-0.0030M1-2.7832M21.3365M37.5062M414.9092\nM520.5289M625.3319M727.6349M825.7213M920.8743M1013.9606M115.3803季节性多元回归方程为：2001年各月份平均气温的预测值如下：年/月时间虚拟变量预测M1M2M3M4M5M6M7M8M9M10M1117310000000000-3.2274010000000000.9375001000000007.14760001000000014.55770000100000020.16780000010000024.97790000001000027.28800000000100025.39810000000010020.410820000000001013.5\n1183000000000014.9128400000000000-0.513.11下表中的数据是一家大型百货公司最近几年各季度的销售额数据（单位：万元）。对这一时间序列的构成要素进行分解，计算季节指数、剔除季节变动、计算剔除季节变动后趋势方程。年/季12341991993.1971.22264.11943.319921673.61931.53927.83079.619932342.42552.63747.54472.819943254.44245.25951.16373.119953904.25105.97252.68630.519965483.25997.38776.18720.619975123.66051.09592.28341.219984942.46825.58900.18723.119995009.96257.98016.87865.620006059.35819.77758.88128.2详细答案：各季节指数如下：1季度2季度3季度4季度季节指数0.75170.85131.23431.1627\n季节变动图如下：根据分离季节因素后的数据计算的趋势方程为：。13.12下表中的数据是一家水产品加工公司最近几年的加工量数据（单位：t）。对该序列进行分解，计算季节指数、剔除季节变动、计算剔除季节变动后趋势方程。年/月19971998199920002001178.891.990.466.899.5278.192.1100.173.380.0384.080.9114.185.3108.4494.394.5108.294.6118.3597.6101.4125.774.1126.86102.8111.7118.3100.8123.3792.792.989.1106.7117.2841.643.646.144.042.09109.8117.5132.1132.1150.610127.3153.1173.9162.5176.611210.3229.4273.3249.0249.212242.8286.7352.1330.8320.6\n详细答案：各月季节指数如下：1月2月3月4月5月6月0.67440.66990.74320.79030.80610.85107月8月9月10月11月12月0.75520.34490.96191.19921.86622.3377季节变动图如下：根据分离季节因素后的数据计算的趋势方程为：。