统计学实习报告

统计学实习报告

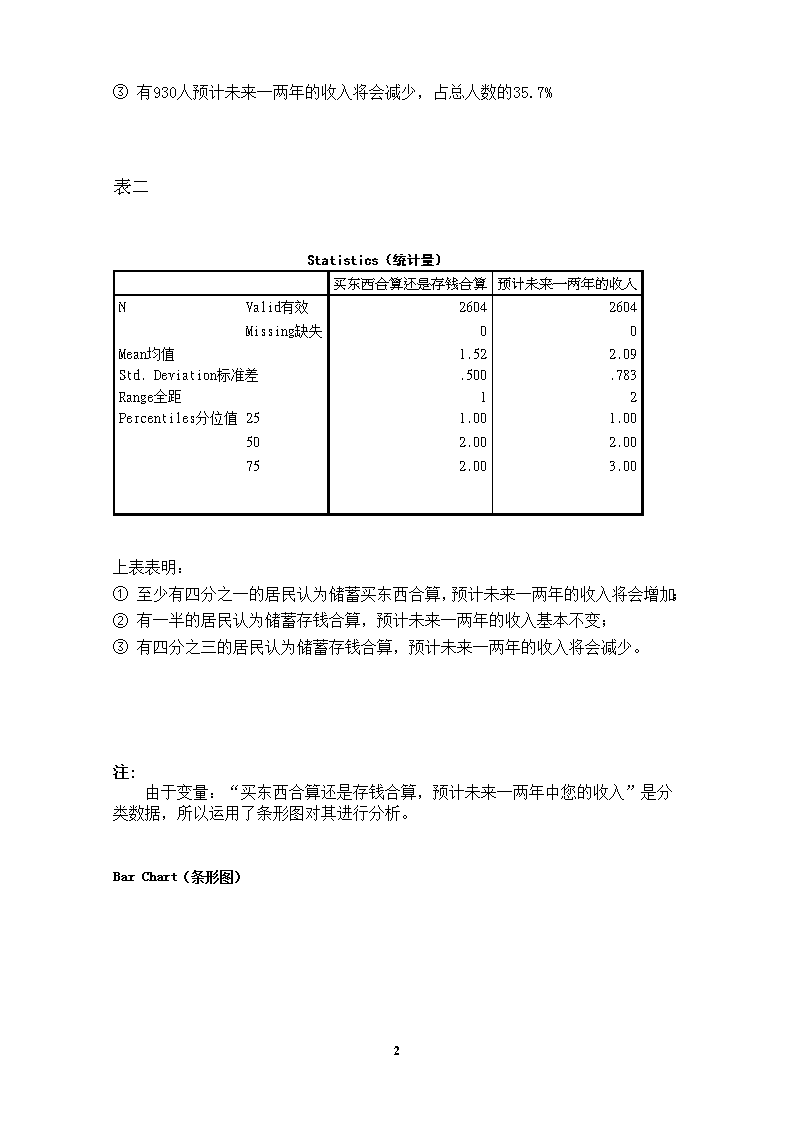
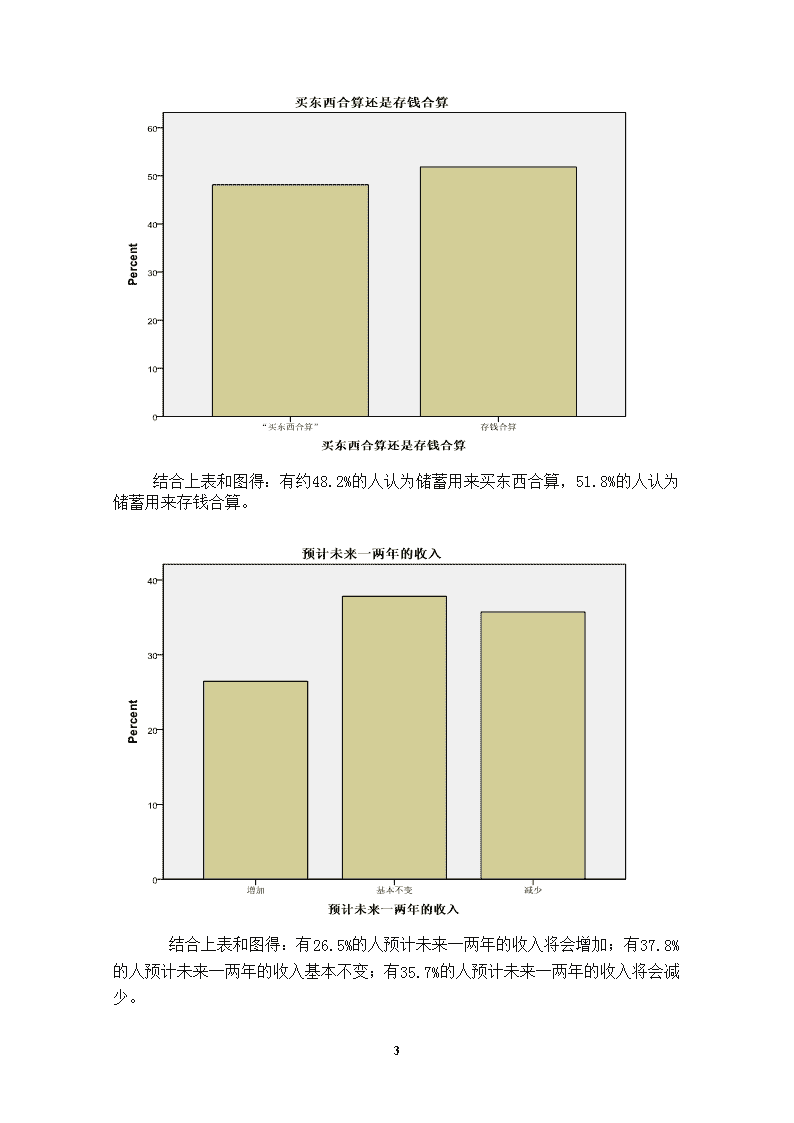
一、频数分析研究题目：从居民调查问卷中研究“现在买东西合算还是存钱合算和预计未来一两年中居民的收入状况”。数据来源：老师提供的统计学实习居民调查问卷数据。主用的统计值：频率、百分比、累计百分比、均值、四分位值分析方法：频数分析表一FrequencyTable（频数分布表）买东西合算还是存钱合算Frequency（频率）Percent（百分比）ValidPercent（有效百分比）CumulativePercent（累计百分比）Valid（有效）“买东西合算”125448.248.248.2存钱合算135051.851.8100.0Total2604100.0100.0上表表明：2604名居民中①有1254人认为储蓄用来买东西合算，占总人数的48.2%，累计百分比是48.2%②有1350人认为储蓄用来存钱合算，占总人数的51.8%预计未来一两年的收入FrequencyPercentValidPercentCumulativePercentValid增加68926.526.526.5基本不变98537.837.864.3减少93035.735.7100.0Total2604100.0100.0上表表明：2604名居民中①有689人预计未来一两年的收入将会增加，占总人数的26.5%②有985人预计未来一两年的收入基本不变，占总人数的37.8%，累计百分比是64.3%17\n①有930人预计未来一两年的收入将会减少，占总人数的35.7%表二Statistics（统计量）买东西合算还是存钱合算预计未来一两年的收入NValid有效26042604Missing缺失00Mean均值1.522.09Std.Deviation标准差.500.783Range全距12Percentiles分位值251.001.00502.002.00752.003.00上表表明：①至少有四分之一的居民认为储蓄买东西合算，预计未来一两年的收入将会增加；②有一半的居民认为储蓄存钱合算，预计未来一两年的收入基本不变；③有四分之三的居民认为储蓄存钱合算，预计未来一两年的收入将会减少。注:由于变量：“买东西合算还是存钱合算，预计未来一两年中您的收入”是分类数据，所以运用了条形图对其进行分析。BarChart（条形图）17\n结合上表和图得：有约48.2%的人认为储蓄用来买东西合算，51.8%的人认为储蓄用来存钱合算。结合上表和图得：有26.5%的人预计未来一两年的收入将会增加；有37.8%的人预计未来一两年的收入基本不变；有35.7%的人预计未来一两年的收入将会减少。17\n一、列联分析研究题目：从居民调查问卷中研究“现在买东西合算还是存钱合算和预计未来一两年中居民的收入状况”。数据来源：老师提供的统计学实习居民调查问卷数据。主用的统计值：卡方、行百分比、列百分比、总百分比、P值分析方法：列联分析表一买东西合算还是存钱合算*预计未来一两年的收入crosstubulation交叉制表预计未来一两年的收入Total合计增加基本不变减少买东西合算还是存钱合算“买东西合算”Count计数3554674321254ExpectedCount期望计数331.8474.3447.91254.0%within买东西合算还是存钱合算28.3%37.2%34.4%100.0%%within预计未来一两年的收入51.5%47.4%46.5%48.2%%ofTotal13.6%17.9%16.6%48.2%Residual23.2-7.3-15.9存钱合算Count3345184981350ExpectedCount357.2510.7482.11350.0%within买东西合算还是存钱合算24.7%38.4%36.9%100.0%%within预计未来一两年的收入48.5%52.6%53.5%51.8%%ofTotal12.8%19.9%19.1%51.8%Residual-23.27.315.9TotalCount6899859302604ExpectedCount689.0985.0930.02604.0%within买东西合算还是存钱合算26.5%37.8%35.7%100.0%%within预计未来一两年的收入100.0%100.0%100.0%100.0%%ofTotal26.5%37.8%35.7%100.0%17\n由上表得：总体情况：参加调查的居民共有2604人，实际观察频数中：（1）1254人认为买东西合算，占总人数的48.2%；1350人认为储蓄用来存钱合算，占总人数的51.8%（2）有689人预计未来一两年的收入将会增加，占总人数的26.5%；有985人预计未来一两年的收入基本不变，占总人数的37.8%；有930人预计未来一两年的收入将会减少，占总人数的35.7%具体情况：（1）认为买东西合算的人共1254人，对未来一两年的收入的看法：355人预计未来一两年的收入将会增加；占买东西合算总人数的28.3%，占增加总人数的51.5%，占总人数的13.6%467人预计未来一两年的收入基本不变；占买东西合算总人数的37.2%，占基本不变总人数的47.4%，占总人数的17.9%432人预计未来一两年的收入减少；占买东西合算总人数的34.4%，占减少总人数的46.5%，占总人数的16.6%（2）认为用来存钱合算的人共1350人，对未来一两年的收入的看法：334人预计未来一两年的收入将会增加；占存钱合算总人数的24.7%，占增加总人数的48.5%，占总人数的12.8%。17\n518人预计未来一两年的收入基本不变；占存钱合算总人数的38.4%，占基本不变总人数的52.6%，占总人数的19.9%。498人预计未来一两年的收入减少；占存钱合算总人数的36.9%，占减少总人数的53.5%，占总人数的19.1%。（3）由此可见：认为买东西合算的人中觉得“未来一两年的收入基本不变”的比例（37.2%）高于觉得“未来一两年收入将会增加（28.3%）或减少（34.4%）”的比例；认为存钱合算的人中觉得“未来一两年的收入基本不变”的比例（38.4%）高于觉得“未来一两年收入将会增加（24.7%）或减少（36.9%）”的比例。说明认为存钱核算的人比认为买东西合算的人更觉“得未来一两年的收入基本不变”且减少的可能性比增加的可能性大。表二卡方检验Chi-SquareTestsValuedfAsymp.Sig.(2-sided)渐近sig(双侧)PearsonChi-Square卡方4.431a2.109LikelihoodRatio似然比4.4302.109Linear-by-LinearAssociation线性和线性组合3.8251.050NofValidCases有效案例中的n2604a.0cells(.0%)haveexpectedcountlessthan5.Theminimumexpectedcountis331.80.此检验有效，a.0单元格的期望计数少于5，最小期望数位331.80.由卡方检验表得：卡方概率p值大于显著性水平（0.05或0.01）接受零假设，即认为“买东西合算还是存钱合算”对“预计未来一两年中的收入”无显著影响。一、单因素方差分析研究题目：管理者的不同水平是否会导致讲座的满意度评分的显著性差异。数据来源：见附录1主用统计值：F统计量、P值、LSD值、均值差分析方法：单因素方差分析17\n表一TestofHomogeneityofVariances方差奇性检验满意度平分LeveneStatisticdf1df2Sig.1.324215.296由以上检验的结果知:检验的P值为0.296，大于显著性水平0.05。则应接受原假设,即各水平下的总体方差无显著差异，满足方差分析的前提。表二ANOVA满意度平分SumofSquaresdfMeanSquareFSig.BetweenGroups组间29.610214.80511.756.001WithinGroups组内18.890151.259Total48.50017由方差分析的结果可知F检验的P值为0.001，小于显著性水平0.05。拒绝原假设，即管理者的水平对评分有显著影响。表三MultipleComparisons多重比较满意度平分LSD(I)管理者层次(J)管理者层次MeanDifference均值差(I-J)Std.Error标准误差显著性Sig.95%ConfidenceInterval置信区间LowerBound下限UpperBounddimension2高级管理者dimension3中级管理者-1.25714.65710.075-2.6577.1434低级管理者1.76667*.67953.020.31833.2151中级管理者dimension3高级管理者1.25714.65710.075-.14342.6577低级管理者3.02381*.62434.0001.69314.3546低级管理者dimension3高级管理者-1.76667*.67953.020-3.2151-.3183中级管理者-3.02381*.62434.000-4.3546-1.6931*.Themeandifferenceissignificantatthe0.05level.显著性水平为0.0517\n由多重比较表可知：①高级管理者与中级管理者的评分之间无显著差异。②高级管理者与低级管理者的评分之间存在显著差异。③中级管理者与低级管理者的评分之间存在显著差异。图一：各个水平下观测变量均值的折线图图一表明：中级管理者与低级管理者的评分之间存在显著差异，且中级管理者与低级管理者的评分之间差异比与高级管理者的差异大。一、相关分析研究题目：广告费用与销售收入之间的关系。数据来源：见附录2分析方法：主运用散点图、相关系数进行分析17\n从上面各散点图可以看出，月销售收入与电视广告费用、报纸广告费用之间都具有一定的线性关系。但，从各散点图的分布情况看，月销售收入与电视广告费用之间的线性关系比较密切。17\n表一Correlations相关性月销售收入电视广告费用报纸广告费用月销售收入PearsonCorrelation1.808*-.021Sig.(2-tailed).015.962N888电视广告费用PearsonCorrelation.808*1-.556Sig.(2-tailed).015.152N888报纸广告费用PearsonCorrelation-.021-.5561Sig.(2-tailed).962.152N888*.Correlationissignificantatthe0.05level(2-tailed).由上表可以看出：在月销售收入与电视广告费用、报纸广告费用两个变量的关系中，与电视广告费用的相关系数（0.808）比较大，与报纸广告费用的相关系数(-0.021)比较小。即月销售收入与电视广告费的线性关系比较密切。五、多元线性回归研究题目：广告费用与销售收入之间的关系。数据来源：见附录2分析方法：多元线性回归分析主运用统计值：R²、调整后的R²、F统计量、P值、回归系数、残差、标准残差、标准估计的误差、标准误差表一VariablesEntered/RemovedaModelVariablesEntered输入的变量VariablesRemoved移去的变量Method方法17\ndimension01电视广告费.Stepwise(Criteria:Probability-of-F-to-enter<=.050,Probability-of-F-to-remove>=.100).2报纸广告费.Stepwise(Criteria:Probability-of-F-to-enter<=.050,Probability-of-F-to-remove>=.100).a.因变量DependentVariable:月销售收入上表表明：（1）本次多元回归分析采用的是逐步筛选法 回归系数显著性F检验的相伴概率值小于0.05的自变量引入了回归方程，大于0.1的自变量剔除出了回归方方程（2）自变量进入回归方程的顺序 首先电视广告费进入回归方程，形成模型1 其次，在模型1的基础上引入第二个自变量—报纸广告费，形成最终的回归模型2 表二ModelSummary模型汇总cModel模型RRSquareR方AdjustedRSquareStd.ErroroftheEstimate标准估计的误差dimension01.808a.653.5951.215182.959b.919.887.64259a.预测变量Predictors:(Constant),电视广告费（万元）b.预测变量Predictors:(Constant),电视广告费（万元）,报纸广告费（万元）c.因变量DependentVariable:月销售收入（万元）由上表得：随着自变量的不断引入回归方程，调整的R2在不断提高，回归方程的估计标准误差在不断减小。 17\n表三ANOVAcModel平方和SumofSquaresdf均方MeanSquareFSig.1Regression回归16.640116.64011.269.015aResidual残差8.86061.477Total总计25.50072Regression23.435211.71828.378.002bResidual2.0655.413Total25.5007a.Predictors:(Constant),电视广告费（万元）b.Predictors:(Constant),电视广告费（万元）,报纸广告费（万元）c.DependentVariable:月销售收入（万元）由上表得：（1）模型1（电视广告费）与模型2(报纸广告费)F检验的P值都小于显著性水平0.05，即因变量销售收入与自变量电视广告费、报纸广告费的线性关系是显著的，即意味着模型中存在多重共线性。（2）第二列的三行分别列出了：回归平方和、剩余平方和、因变量的总平方和。 第四列是第二列除以第三列自由度的结果，分别为平均的回归平方和、平均的剩余平方和。第五列是用于回归方程显著性检验的F统计量，由平均的回归平方和除以平均的剩余平方和得到。第六列是F统计量对应的相伴概率值。 表四Coefficients系数aModelUnstandardizedCoefficients非标准化系数StandardizedCoefficients标准系数tSig.CollinearityStatistics共线性统计量BStd.Error标准误差Beta试用版ToleranceVIF1(Constant)88.6381.58256.016.000电视广告费1.604.478.8083.357.0151.0001.0002(Constant)83.2301.57452.882.000电视广告费2.290.3041.1537.532.001.6901.448报纸广告费1.301.321.6214.057.010.6901.448a.因变量DependentVariable:月销售收入分析系数表得：（1）第一列，是回归分析过程中形成的两个模型的代码和引入自变量的情况，模型2是最终的回归模型；第二列，回归模型各自变量的回归系数，依据该回归系数，案例最终的回归方程为： 17\n销售收入＝83.230+2.290电视广告费+1.301报纸广告费第三列，回归系数的标准误差；第四列，标准化回归系数，可以衡量自变量对因变量的贡献程度。依据标准化回归系数，案例最终的标准化回归方程为： 销售收入＝1.153电视广告费+0.621报纸广告费（2）可见，在其他变量保持一定的条件下：电视广告费增加一个单位，将引起销售收入平均增加1.153个单位；报纸广告费增加一个单位，将引起销售收入平均增加0.621个单位。（3）第五、六列，各回归系数显著性检验的t统计量和其相应的相伴概率值 回归系数的P值均小于显著性水平0.05。应拒绝回归系数显著性检验的零假设， 即认为这些回归系数与零有显著差异，相应的自变量能够较好的解释说明因变量的变化，应该保留在回归方程中。表五以排除的变量ExcludedVariablesbModel模型BetaIntSig.PartialCorrelation偏相关CollinearityStatistics共线性统计量ToleranceVIFMinimumTolerance容差1报纸广告费.621a4.057.010.876.6901.448.690a.PrCollinearityDiagnosticsaModelDimensionEigenvalueConditionIndexVarianceProportions(Constant)电视广告费报纸广告费dimension01dimension111.9621.000.02.022.0387.228.98.982dimension112.8461.000.00.01.012.1404.510.00.16.293.01414.4941.00.83.71a.DependentVariable:月销售收入模型中的预测变量：（常量）edictorsintheModel:(Constant),电视广告费b.DependentVariable:月销售收入17\n上表表明：（1）该表是回归分析过程中，尚未被引入方程的自变量的情况。（2）第二、三、四列，模型1；第二列表示：如果下一步引入报纸广告费，那么它的标准化系数应该是0.621，这个数据与输出结果表四中的模型2是相吻合的。第三、四列表示，如果下一步引入某自变量进入回归方程，它的回归系数显著性检验的t值和对应的相伴概率值。（3）第五列，在控制了方程中已有自变量的前提下计算出的某自变量与因变量的偏相关系数。第六列，显示如果某自变量进入了回归方程，方程中所有自变量容忍度的最小值，通过比较最小容忍度和该自变量的容忍度，可以对目前方程中自变量共线性的大小程度有所把握。 表六残差统计量ResidualsStatisticsaMinimum极小值Maximum极大值Mean均值Std.Deviation标准偏差NPredictedValue预测值90.412496.632593.75001.829738Std.PredictedValue标准预测值-1.8241.575.0001.0008Residual残差值-.63249.65769.00000.543098Std.Residual标准残差值-.9841.024.000.8458Stud.Residual-1.6251.225-.1481.1378DeletedResidual-1.72313.94145-.269921.037088Stud.DeletedResidual-2.1151.309-.1911.2648Mahal.Distance.0483.7471.7501.6218Cook'sDistance.0091.517.434.5378CenteredLeverageValue.007.535.250.2328a.DependentVariable:月销售收入表六表示：残差统计量，第一至第四行数据分别为：根据回归方程计算出的因变量预测值序列、残差序列、标准化预测值序列、标准化残差序列的最小值、最大值、均值、标准差和样本数。17\n残差分析结果 （1）标准化残差直方图： 从图中看出，标准化残差不服从均值为0的正态分布，图形略呈右偏分布。（2）标准化残差散点图：标准化残差在0附近波动，残差的均值为0；但17\n并不是随机的分布在一条平行的带子内，图形有点关于X轴对称。（3）方差为常数，且残差之间不相关，95%的点分布在-1至+1之间。（4）综上所述，标准化残差不服从标准正态分布，即随机误差项不服从基本假定。 总结：1、本次实习中所进行的定量分析的研究题目、数据来源及定量分析的方法：(1)第一个研究题目：从居民调查问卷中研究“现在买东西合算还是存钱合算和预计未来一两年中居民的收入状况”。数据来源：老师提供的统计学实习居民调查问卷数据。分析方法：对其进行频数分析、绘制了条形图进行分析、列联分析(2)第二个研究题目：管理者的不同水平是否会导致讲座的满意度评分的显著性差异。数据来源：贾俊平主编的《统计学》教材，第293页习题10.4分析方法：单因素方差分析(3)第三个研究题目：广告费用与销售收入之间的关系。数据来源：贾俊平主编的《统计学》教材，第359页习题12.4分析方法：相关分析、多元线性回归分析2、对SPSS软件输出结果的分析（祥见报告）3、对本次实习定量分析工作的评价（1）在这次实习中，我通过学习和运用SPSS软件对想研究的题目进行分析后，觉得仅学习课本知识是不够的，还是要通过实践来加深对所学知识理论的理解和运用。（2）通过对照这次的定量分析的内容，我觉得这次分析基本上达到了原先研究设计的目的。了解到：①居民储蓄问卷调查中，大多数居民认为储蓄用来存钱合算且预计未来一两年的收入将基本不变，且认为存钱核算的居民比认为买东西合算的居民更觉得“未来一两年的收入将基本不变”且减少的可能性比增加的可能性大。②管理者的水平对评分有显著影响，且中级管理者与低级管理者的评分之间差异比与高级管理者的差异大。③销售收入与电视广告费、报纸广告费的线性关系是显著的。（3）本次研究的长处：对数据有较详细的分析，对问题有了更深的了解，对各变量之间的关系有了新的发现。不足：只会软件的一部分应用，有一些统计数据所代表的含义不是很清楚，对数据进行的一些分析可能是不正确的，自己所总结一些结论可能是不正确的。17\n附录：一、附录1———单因素方差分析原始数据数据源：贾俊平主编的《统计学》第四版，中国人民大学出版社，第293页习题10.4管理者层次111112222222333333满意度平分77879898109108565748注：1=“高级管理者”；2=“中级管理者”；3=“低级管理者”二、附录2———相关分析、多元线性回归分析原始数据数据源：贾俊平主编的《统计学》第四版，中国人民大学出版社，第359页习题12.4月销售收入电视广告费用报纸广告费用965.01.5902.02.0954.01.5922.52.5953.03.3943.52.3942.54.2943.02.517