- 2022-08-13 发布 |
- 37.5 KB |
- 13页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
统计学答案解析
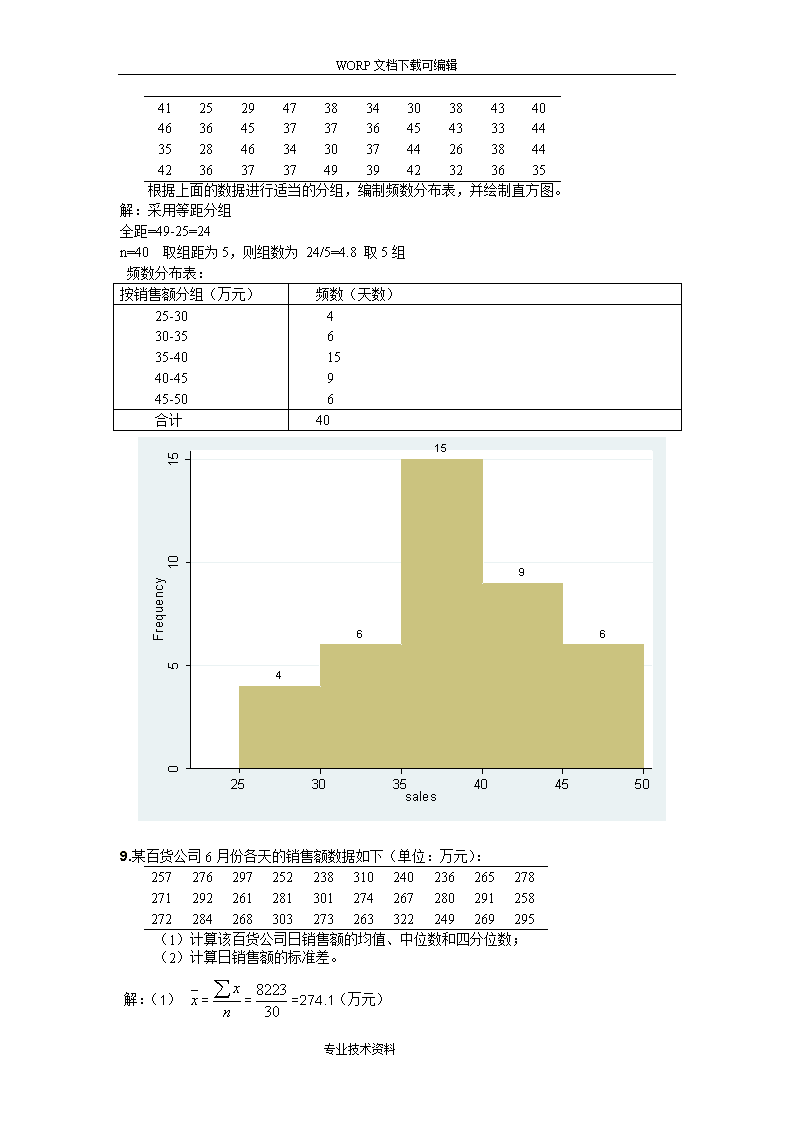
WORP文档下载可编辑统计学课本课后作业题(全)题目:第1章:P116,7第2章:P52练习题3、9、10、11第3章:P116思考题12、14练习题16、25第4章:P114思考题6,练习题2、4、6、13第5章:P179思考题4、练习题3、4、6、11第6章:P209思考题4、练习题1、3、6第7章:P246思考题1、练习题1、7第8章:P287思考题4、10练习题2、3第一章6..一家大型油漆零售商收到了客户关于油漆罐分量不足的许多抱怨。因此,他们开始检查供货商的集装箱,有问题的将其退回。最近的一个集装箱装的是2440加仑的油漆罐。这家零售商抽查了50罐油漆,每一罐的质量精确到4位小数。装满的油漆罐应为4.536kg。要求:(1)描述总体;最近的一个集装箱内的全部油漆;(2)描述研究变量;装满的油漆罐的质量;(3)描述样本;最近的一个集装箱内的50罐油漆;(4)描述推断。50罐油漆的质量应为4.536×50=226.8kg。7.“可乐战”是描述市场上“可口可乐”与“百事可乐”激烈竞争的一个流行术语。这场战役因影视明星、运动员的参与以及消费者对品尝试验优先权的抱怨而颇具特色。假定作为百事可乐营销战役的一部分,选择了1000名消费者进行匿名性质的品尝试验(即在品尝试验中,两个品牌不做外观标记),请每一名被测试者说出A品牌或B品牌中哪个口味更好。要求:答:(1)总体:市场上的“可口可乐”与“百事可乐”(2)研究变量:更好口味的品牌名称;(3)样本:1000名消费者品尝的两个品牌(4)推断:两个品牌中哪个口味更好。第二章3.某百货公司连续40天的商品销售额如下(单位:万元):专业技术资料\nWORP文档下载可编辑41252947383430384340463645373736454333443528463430374426384442363737493942323635根据上面的数据进行适当的分组,编制频数分布表,并绘制直方图。解:采用等距分组全距=49-25=24n=40取组距为5,则组数为24/5=4.8取5组频数分布表:按销售额分组(万元)频数(天数)25-3030-3535-4040-4545-50461596合计409.某百货公司6月份各天的销售额数据如下(单位:万元):257276297252238310240236265278271292261281301274267280291258272284268303273263322249269295(1)计算该百货公司日销售额的均值、中位数和四分位数;(2)计算日销售额的标准差。解:(1)===274.1(万元)专业技术资料\nWORP文档下载可编辑将30个数据重新排序,则中位数位于30个数据的中间位置,即靠中的第15、第16两个数272和273的平均数:Me==272.5(万元)由于中位数位于第15个数靠上半位的位置上,所以前四分位数位于第1~第15个数据的中间位置(第8位)靠上四分之一的位置上,由重新排序后的第8位是261,第15位是272,从而:QL=261+=261.25(万元)同理,后四分位数位于第16~第30个数据的中间位置(第23位)靠下四分之一的位置上,由重新排序后第23位是291,第16位是273,从而:QU=291-=290.75(万元)。(2)未分组数据的标准差计算公式为:s=得s=21.1742。10.甲乙两个企业生产三种产品的单位成本和总成本资料如下:产品名称单位成本(元)总成本(元)甲企业乙企业ABC152030210030001500325515001500比较哪个企业的总平均成本高?并分析其原因。解:设产品单位成本为x,产量为f,则总成本为xf,由于:平均成本==,而已知数据中缺产量f的数据,又因个别产品产量f==从而=,于是得:甲企业平均成本===19.41(元),乙企业平均成本===18.29(元),对比可见,甲企业的总平均成本较高。原因:尽管两个企业的单位成本相同,但单位成本较低的产品在乙企业的产量中所占比重较大,因此拉低了总平均成本。11.在某地区抽取的120家企业按利润额进行分组,结果如下:按利润额分组(万元)企业数(个)200~30019300~40030专业技术资料\nWORP文档下载可编辑400~50042500~60018600以上11合计120计算120家企业利润额的均值和标准差。解:设各组平均利润为x,企业数为f,则组总利润为xf,由于数据按组距式分组,须计算组中值作为各组平均利润,列表计算得:按利润额分组(万元)组中值企业数(个)总利润xfxf200~300250194750300~4003503010500400~5004504218900500~600550189900600以上650117150合计—12051200于是,120家企业平均利润为:===426.67(万元);s===116.48(万元)。第3章思考练习:12解析总体分布、样本分布和抽样分布的含义总体分布:就是与总体相联系的随机变量的概率分布样本分布:是与样本相联系的随机向量的联合概率分布抽样分布:就是作为样本的函数的统计量的分布14解析中心极限定理的含义:是阐述大量随机变量之和的分布趋近于正态分布的一系列定理的总称。16某企业生产的某种电池寿命近似服从正态分布,且均值为200小时,标准差为30小时若规定寿命低于150小时为不合格品。试求(1)该企业生产的电池的合格率是多少?(2)该企业生产的寿命在200小时左右的多大范围内的概率不小于0.9?解(1)=0.04779合格率为1-0.04779=0.95221或95.221%。(2)设所求值为K,满足电池寿命在200±K小时范围内的概率不小于0.9,即有:即:,K/30≥1.64485,故K≥49.3456。25某制造商为击剑运动员生产安全夹克,这些夹克是以剑锋刺入其中时所需的最小力量(以牛顿为单位)来定级的。如果生产工艺操作正确,则他生产的夹克级别应平均840专业技术资料\nWORP文档下载可编辑牛顿,标准差15牛顿。国际击剑管理组织(FIE)希望这些夹克的最低级别不小于800牛顿。为了检查其生产过程是否正常,某检验人员从生产过程中抽取了50个夹克作为一个随机样本进行定级,并计算,即该样本中夹克级别的均值。她假设这个过程的标准差是固定的,但是担心级别均值可能已经发生变化。⑴如果该生产过程仍旧正常,则的样本分布为何?⑵假设这个检验人员所抽取样本的级别均值为830牛顿,则如果生产过程正常的话,样本均值≤830牛顿的概率是多少?⑶在检验人员假定生产过程的标准差固定不变时,你对b部分有关当前生产过程的现状有何看法(即夹克级别均值是否仍为840牛顿)?⑷现在假设该生产过程的均值没有变化,但是过程的标准差从15牛顿增加到了45牛顿。在这种情况下的抽样分布是什么?当具有这种分布时,则≤830牛顿的概率是多少?第四章参数估计6简述样本量与置信水平、总体方差、允许误差的关系。样本容量与置信水平成正比、与总体方差成正比、与允许误差成反比2.某快餐店想要估计每位顾客午餐的平均花费金额,在为期3周的时间里选取49名顾客组成了一个简单随机样本。(1)假定总体标准差为15元,求样本均值的抽样标准误差;(2)在95%的置信水平下,求允许误差;(3)如果样本均值为120元,求总体均值95%的置信区间。解:(1)已假定总体标准差为=15元则样本均值的抽样标准误差为===2.1429(2)已知置信水平1-=95%,得=1.96,于是,允许误差是E==1.96×2.1429=4.2000。(3)已知样本均值为=120元,置信水平1-=95%,得=1.96,这时总体均值的置信区间为=120±4.2=可知,如果样本均值为120元,总体均值95%的置信区间为(115.8,124.2)元。4.从一个正态总体中随机抽取容量为8的样本,各样本值分别为:10,8,12,15,6,13,5,11。求总体均值95%的置信区间。解:(7.1,12.9)。6.在一项家电市场调查中,随机抽取了200个居民户,调查他们是否拥有某一品牌的电视机。其中拥有该品牌电视机的家庭占23%。求总体比率的置信区间,置信水平分别为90%和95%。解:已知样本容量n=200,为大样本,拥有该品牌电视机的家庭比率p=23%,拥有该品牌电视机的家庭比率的抽样标准误差为===2.98%专业技术资料\nWORP文档下载可编辑⑴双侧置信水平为90%时,通过2-1=0.90换算为单侧正态分布的置信水平=0.95,查单侧正态分布表得=1.64,此时的置信区间为=23%±1.64×2.98%=可知,当置信水平为90%时,拥有该品牌电视机的家庭总体比率的置信区间为(18.11%,27.89%)。⑵双侧置信水平为95%时,得=1.96,此时的置信区间为=23%±1.96×2.98%=可知,当置信水平为95%时,拥有该品牌电视机的家庭总体比率的置信区间为;(17.16%,28.84%)。13.根据以往的生产数据,某种产品的废品率为2%。如果要求95%的置信区间,若要求允许误差不超过4%,应抽取多大的样本?解:已知总体比率=2%=0.02,由置信水平1-α=95%,得置信度=1.96,允许误差E≤4%即由允许误差公式E=整理得到样本容量n的计算公式:n===≥=47.0596由于计算结果大于47,故为保证使“≥”成立,至少应取48个单位的样本。第五章4什么是P值?P值检验决策的意义是什么?答:p值是当原假设为真时,检验统计量小于或等于根据实际观测样本数据计算得到的检验统计量值的概率。P值常常作为观察到的数据与原假设不一致程度的度量。统计量检验采用事先确定显著性水平,来控制犯第一类错误的上限,p值可以有效地补充提供地关于检验可靠性的有限信息。值检验的优点在于,它提供了更多的信息,让人们可以选择一定的水平来评估结果是否具有统计上的显著性。3一家大型超市连锁店上个月接到许多消费者投诉某种品牌炸土豆片中60g一袋的那种土豆片的重量不符合。店方猜想引起这些投诉的原因是运输过程中沉积在食品袋底部的土豆片碎屑,但为了使顾客们对花钱买到的土豆片感到物有所值,店方仍然决定对来自于一家最大的供应商的下一批袋装炸土豆片的平均重量(g)u进行检验,假设陈述如下:Ho:u>=60H1:u<60(1)与这一假设检验问题相关联的第I类错误是什么?(2)与这一假设检验问题相关联的第II类错误是什么?(3)你认为连锁店的顾客们会将哪类错误看得较为严重?而供应商会将哪类错误看得较为严重?专业技术资料\nWORP文档下载可编辑(1)第一类错误是该供应商提供的这批炸土豆片的平均重量的确大于等于60克,但检验结果却提供证据支持店方倾向于认为其重量少于60克;(2)第二类错误是该供应商提供的这批炸土豆片的平均重量其实少于60克,但检验结却没有提供足够的证据支持店方发现这一点,从而拒收这批产品;(3)连锁店的顾客们自然看重第二类错误,而供应商更看重第一类错误。4某种纤维原有平均强度不超过6g,现希望通过改进工艺来提高其平均强度。研究人员测得了100个关于新纤维的强度数据,发现其均值为6.35。假定纤维强度的标准差仍保持为1.19不变,在5%的显著性水平下对该问题进行假设检验。(1)选择检验统计量并说明其抽样分布是什么样的。(2)检验的拒绝规则是什么?(3)计算检验统计量的值,你的结论是什么?(1)检验统计量,在大样本情形下近似服从标准正态分布;(2)如果,就拒绝;(3)检验统计量=2.94>1.645,所以应该拒绝。。6一个视频录像设备(VCR)的平均使用寿命为6年,标准差为0.75年,而抽选了由30台电视组成的一个随机样本表明,电视使用寿命的样本方差为2年。试构造一个假设检验,能够帮助判定电视的使用寿命的方差是否显著大于视频录像设备的使用寿命的标准差,并在a=0.05的显著性水平下作出结论。解:提出假设已知:检验统计量拒绝,可判定电视使用寿命的方差显著大于VCR11为比较新旧两种肥料对产量的影响,一边决定是否采用新肥料。研究者选择了面积相等、土壤等条件相同的40块田地,分别施用新旧两种肥料,得到的产量数据如下表。旧肥料新肥料10910197981009898949910410388108102106971051021041011051091101181091131111119911210611799107119110111103110119取显著性水平a=0.05,用Excel检验(1)检验结果如下:t-检验:双样本等方差假设 变量1变量2平均100.7109.9专业技术资料\nWORP文档下载可编辑方差24.1157894733.35789474观测值2020合并方差28.73684211假设平均差0df38tStat-5.427106029P(T<=t)单尾1.73712E-06t单尾临界1.685953066P(T<=t)双尾3.47424E-06t双尾临界2.024394234 t-检验:双样本异方差假设 变量1变量2平均100.7109.9方差24.1157894733.35789474观测值2020假设平均差0df37tStat-5.427106029P(T<=t)单尾1.87355E-06t单尾临界1.687094482P(T<=t)双尾3.74709E-06t双尾临界2.026190487 (2)方差检验结果如下:F-检验双样本方差分析 变量1变量2平均100.7109.9方差24.1157894733.35789474观测值2020df1919F0.722940991P(F<=f)单尾0.243109655F单尾临界0.395811384第六章4简述方差分析的基本思想。是对比不同影响水平下整体方差和组间方差的差异,即不同水平的数据间方差和随机方差的对比1从三个总体中各抽取容量不同样本数据,得到的资料见表。检验3个总体的均值之间是否有显著差异。(a=0.01)三个总体抽取的样本数据样本1样本二样本三专业技术资料\nWORP文档下载可编辑158148161154169153142156149169158180(或),不能拒绝原假设。3某企业准备用三种方法组装一种新的产品,为确定哪种方法每小时生产的产品数量最多,随机抽取了30名工人,并指定每个人使用其中的一种方法。通过对每个工人生产的产品数进行方差分析得到的结果(1)完成下面的方差分析表方差分析表中所缺的数值如下表:差异源SSdfMSFP-valueFcrit组间42022101.4780.2459463.354131组内383627142.07———总计425629————(2)若显著性水平a=0.05,检验三种方法组装的产品数量之间是否有显著差异。(或),不能拒绝原假设。6为检验广告媒体和广告方案对产品销售的影响,一家营销公司做了一项试验,考察三种广告方案和两种广告媒体,获得的销售数据如表。广告方案广告媒体报纸电视A812128B22142630C10181814检验广告方案、广告媒体或其交互作用对销售量的影响是否显著。(a=0.05)(或),拒绝原假设。(或),不能拒绝原假设。(或),不能拒绝原假设。第七章1相关分析与回归分析的区别和联系是什么?答:相关与回归分析是研究变量之间不确定性统计关系的重要方法,相关分析主要是判断两个或两个以上变量之间是否存在相关关系,并分析变量间相关关系的形态和程度。回归分析主要是对存在相关关系的现象间数量变化的规律性作出测度。但它们在研究目的和对变量的处理上有明显区别。它们均是统计方法,不能揭示现象之间的本质关系。专业技术资料\nWORP文档下载可编辑1.设销售收入x为自变量,销售成本y为因变量。现已根据某百货公司某年12个月的有关资料计算出以下数据(单位:万元):(1)拟合简单西线性回归方程,并对方程中回归系数的经济意义作出结解析(2)计算可决系数和回归估计的标准方差(3)对B2进行显著性水平为5%的显著性检验(4)假定下年一月销售收入为800万元,利用拟合的回归方程预测其销售成本,并给出置信度为95%的预测区间。解:设简单线性回归方程为:(1)采用OLS估计:回归系数经济意义:销售收入每增加1万元,销售成本会增加0.786万元。(2)可决系数为:回归标准误:(3)检验统计量为:所以是显著不为零(4)预测:95%的预测区间为:即(664.579,674.153)7.表中给出对和回归的结果:多元性回归的结果离差来源平方和()自由度()平方和的均值()来自回归()65965专业技术资料\nWORP文档下载可编辑来自残差()总离差()6604214(1)该回归分析中样本容量是多少?(2)计算;(3)和的自由度是多少?(4)计算可决系数和修正的可决系数;(5)怎样检验和对是否有显著影响?根据以上信息能否确定和各自对的贡献为多少?解:(1)该回归分析中样本容量是14+1=15(2)计算RSS=66042-65965=77ESS的自由度为k-1=2,RSS的自由度n-k=15-3=12(3)计算:可决系数修正的可决系数(4)检验X2和X3对Y是否有显著影响(5)F统计量远比F临界值大,说明X2和X3联合起来对Y有显著影响,但并不能确定X2和X3各自对Y的贡献为多少。第八章4甲企业近四年产品销售产量分别增长了9%、7%、8%、6%,乙企业这四年产品的次品率也正好是9%、7%、8%、6%。这两个企业这四年的平均增长率和平均次品率的计算是否一样?为什么?10循环变动和季节变动的区别是什么?循环变动与季节变动的区别是,循环变动的周期长短很不一致,不像季节变动那样有明显的按月或按季的固定周期规律,循环变动的规律性不甚明显。2.某地区社会商品零售额1988—1992(1993—1997)年期间(1987(1992)年为基期)每年平均增长10%,1993—1997(1998—2002)年期间每年平均增长8.2%,1998—2003(2003—2008)年期间每年平均增长6.8%。问2003年与1987年相比该地区社会商品零售额共增长多少?年平均增长速度是多少?若1997(2002)年社会商品零售额为30亿元,按此平均增长速度,2004(2009)年的社会商品零售额应为多少?(注意:上面的年份和书本是不一样的,但数据一样。把年份改过来就行了,括号里面的年份是书本的。)解:设i年的环比发展水平为xi,则已知的三段年均增长率表示为:专业技术资料\nWORP文档下载可编辑,即为,即为,即为于是得:(1)以1987年为基期,2003年与1987年相比,该地区社会商品零售额的发展速度为:==从而得知,2003年与1987年相比,该地区社会商品零售额共增长254.43%。(2)1987年至2003年之间,年平均发展速度为:==1.0822945=108.23%可知,1987年至2003年之间,年平均增长速度为8.23%。(3)若x1997=30亿元,按平均增长速度8.23%计算x2004,即由得x2004=(亿元)可知,按照假定,2004年的社会商品零售额应为52.1867亿元3某地区国内生产总值在1998—2000年平均每年递增12%,2001—2004年平均每年递增10%,2005——2007年平均每年递增8%。试计算(1)该地区国内生产总值在这10年间的发展总速度和平均增长速度;(2)若2007年的国内生产总值为500亿元,以后平均每年增长6%,到2009年可达多少?(3)若2009年的国内生产总值计划任务为570亿元,一季度的季节比率为15%.则2009年一季度的计划任务应为多少?(1)发展总速度平均增长速度=(2)(亿元)专业技术资料\nWORP文档下载可编辑(3)平均数(亿元),2002年一季度的计划任务:(亿元)。专业技术资料查看更多