医学统计学方法
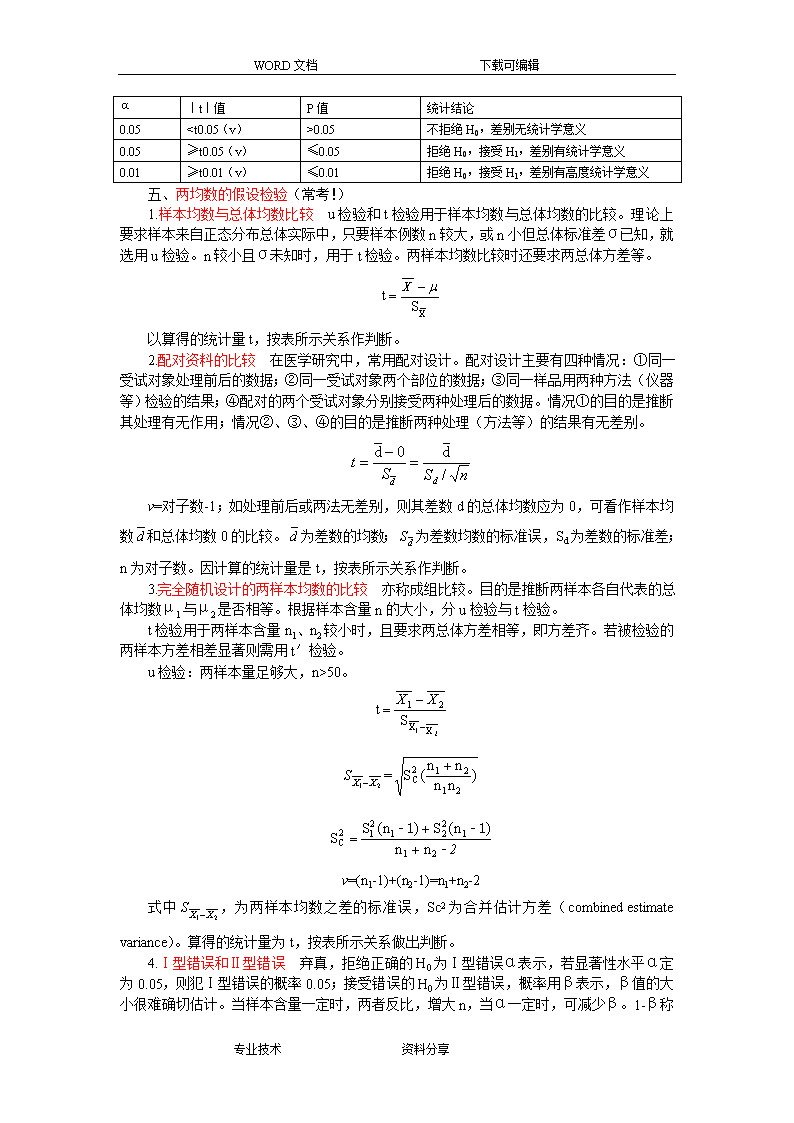
WORD文档下载可编辑医师资格考试蓝宝书-预防医学医学统计学方法第一节基本概念和基本步骤(非常重要)一、统计工作的基本步骤设计(最关键、决定成败)、搜集资料、整理资料、分析资料。总体:根据研究目的决定的同质研究对象的全体,确切地说,是性质相同的所有观察单位某一变量值的集合。总体的指标为参数。实际工作中,经常是从总体中随机抽取一定数量的个体,作为样本,用样本信息来推断总体特征。样本的指标为统计量。由于总体中存在个体变异,抽样研究中所抽取的样本,只包含总体中一部分个体,这种由抽样引起的差异称为抽样误差。抽样误差愈小,用样本推断总体的精确度愈高;反之,其精确度愈低。某事件发生的可能性大小称为概率,用P表示,在0~1之间,0和1为肯定不发生和肯定发生,介于之间为偶然事件,<0.05或0.01为小概率事件。二、变量的分类变量:观察单位的特征,分数值变量和分类变量。第二节数值变量数据的统计描述(重要考点)一、描述计量资料的集中趋势的指标有1.均数均数是算术均数的简称,适用于正态或近似正态分布。2.几何均数适用于等比资料,尤其是对数正态分布的计量资料。对数正态分布即原始数据呈偏态分布,经对数变换后(用原始数据的对数值lgX代替X)服从正态分布,观察值不能为0,同时有正和负。3.中位数一组按大小顺序排列的观察值中位次居中的数值。可用于描述任何分布,特别是偏态分布资料的集中位置,以及分布不明或分布末端无确定数据资料的中心位置。不能求均数和几何均数,但可求中位数。百分位数是个界值,将全部观察值分为两部分,有X%比小,剩下的比大,可用于计算正常值范围。二、描述计量资料的离散趋势的指标1.全距和四分位数间距。2.方差和标准差最为常用,适于正态分布,既考虑了离均差(观察值和总体均数之差),又考虑了观察值个数,方差使原来的单位变成了平方,所以开方为标准差。均为数值越小,观察值的变异度越小。3.变异系数多组间单位不同或均数相差较大的情况。变异系数计算公式为:CV=s/×100%,公式中s为样本标准差,为样本均数。三、标准差的应用表示观察值的变异程度(或离散程度)。在两组(或几组)资料均数相近、度量单位相同的条件下,标准差大,表示观察值的变异度大,即各观察值离均数较远,均数的代表性较差;反之,表示各观察值多集中在均数周围,均数的代表性较好。(常考!)四、医学参考值的计算方法,单双侧问题,医学为95%专业技术资料分享\nWORD文档下载可编辑医学参考值是指正常人体或动物体的各种生理常数,由于存在变异,各种数据不仅因人而异,而且同一个人还会随机体内外环境的改变而改变,因而需要确定其波动的范围,即正常值范围。医学参考值的计算公式:①正态分布资料95%医学参考值:±1.96s(双侧);+1.645s或-1.645s(单侧),s为标准差。②百分位数法P2.5和P97.5(双侧);P5或P95(单侧)。第三节数值变量数据的统计推断(重要考点)一、标准误,标准误与标准差和样本含量的关系标准差和标准误的区别。样本标准误等于样本标准差除以根号下样本含量。标准误与标准差成正比;与样本含量的平方根成反比。因此。为减少抽样误差,应尽可能保证足够大的样本含量。样本标准差与样本标准误是既有联系又有区别的两个统计量,二者的联系是公式:二者的区别在于:样本标准差是反映样本中各观测值X1,X2,……,Xn变异程度大小的一个指标,它的大小说明了对该样本代表性的强弱。样本标准误是样本平均数1,2,……的标准差,它是抽样误差的估计值,其大小说明了样本间变异程度的大小及精确性的高低。(掌握!)二、t分布和标准正态u分布关系均以0为中心左右两侧完全对称的分布,只是t分布曲线顶端较u分布低,两端翘。(v逐渐增大,t分布逐渐逼近u分布)。正态分布的特点:①以均数为中心左右两侧完全对称分布;②两个参数,均数u(位置参数)和s(变异参数);③对称均数的两侧面积相等。三、总体均数的估计样本统计量推算总体均数有两个重要方面:区间估计和假设检验。样本均数估计总体均数称点估计。总体均数区间估计(可信区间)的概念:按一定的可信度估计未知总体均数所在范围。其统计上习惯用95%(或99%)可信区间表示总体均数μ有95%(或99%)的可能在某一范围。可信区间的两个要素,一为准确度,反映在可信度1-α的大小,即区间包含总体均数的概率大小,当然愈接近1愈好;二是精度,反映在区间的长度,当然长度愈小愈好。在样本例数确定的情况下,二者是矛盾的,需要兼顾。总体均数可信区间的计算方法:1.当n小按t分布的原理用式计算可信区间为:±tα/2,vS2.当n足够大因n足够大时,t分布逼近μ分布,按正态分布原理。用式估计可信区间为:±μα/2S可信区间与医学参考值范围的区别:二者的意义和算法不同。四、假设检验的步骤1.建立假设:H0(无效,两样本代表的总体均数相同),H1(备择,两样本来自不同总体),当拒绝H0就接受H1,不拒绝就不接受H1。2.确定显著性水平:区分大概率和小概率事件的标准,通常取α=0.05。3.计算统计量:根据资料类型和分析目的选择适当的公式计算。4.确定概率P值:将计算得到的t值或u值查界值表得到P值和α值比较。5.做出推断结论。|t|值、P值与统计结论专业技术资料分享\nWORD文档下载可编辑α|t|值P值统计结论0.05
0.05不拒绝H0,差别无统计学意义0.05≥t0.05(v)≤0.05拒绝H0,接受H1,差别有统计学意义0.01≥t0.01(v)≤0.01拒绝H0,接受H1,差别有高度统计学意义五、两均数的假设检验(常考!)1.样本均数与总体均数比较u检验和t检验用于样本均数与总体均数的比较。理论上要求样本来自正态分布总体实际中,只要样本例数n较大,或n小但总体标准差σ已知,就选用u检验。n较小且σ未知时,用于t检验。两样本均数比较时还要求两总体方差等。以算得的统计量t,按表所示关系作判断。2.配对资料的比较在医学研究中,常用配对设计。配对设计主要有四种情况:①同一受试对象处理前后的数据;②同一受试对象两个部位的数据;③同一样品用两种方法(仪器等)检验的结果;④配对的两个受试对象分别接受两种处理后的数据。情况①的目的是推断其处理有无作用;情况②、③、④的目的是推断两种处理(方法等)的结果有无差别。v=对子数-1;如处理前后或两法无差别,则其差数d的总体均数应为0,可看作样本均数和总体均数0的比较。为差数的均数;为差数均数的标准误,Sd为差数的标准差;n为对子数。因计算的统计量是t,按表所示关系作判断。3.完全随机设计的两样本均数的比较亦称成组比较。目的是推断两样本各自代表的总体均数μ1与μ2是否相等。根据样本含量n的大小,分u检验与t检验。t检验用于两样本含量n1、n2较小时,且要求两总体方差相等,即方差齐。若被检验的两样本方差相差显著则需用t′检验。u检验:两样本量足够大,n>50。=v=(n1-1)+(n2-1)=n1+n2-2式中,为两样本均数之差的标准误,Sc2为合并估计方差(combinedestimatevariance)。算得的统计量为t,按表所示关系做出判断。4.Ⅰ型错误和Ⅱ型错误弃真,拒绝正确的H0为Ⅰ型错误α表示,若显著性水平α定为0.05,则犯Ⅰ型错误的概率0.05;接受错误的H0为Ⅱ型错误,概率用β表示,β值的大小很难确切估计。当样本含量一定时,两者反比,增大n,当α一定时,可减少β。1-β专业技术资料分享\nWORD文档下载可编辑称为检验效能或把握度,其统计意义是若两总体确有差别,按α水准能检出其差别的能力。客观实际拒绝H0不拒绝H0H0成立Ⅰ型错误(α)推断正确1-αH0不成立推断正确(1-β)Ⅱ型错误(β)5.假设检验注意事项保证组间可比性;根据研究目的、资料类型和设计类型选用适当的检验方法,熟悉各种检验方法的应用条件;“显著与否”是统计学术语,为“有无统计学意义”,不能理解为“差别是不是大”;结论不能绝对化。第四节分类变量资料的统计描述(一般考点)相对数是两个有关联事物数据之比。常用的相对数指标有构成比、率、相对比等。一、构成比表示事物内部各个组成部分所占的比重,通常以100为例基数,故又称为百分比。其公式如下:构成比=×100%该式可用符号表达如下:构成比=×100%构成比有两个特点:(1)各构成部分的相对数之和为100%.(2)某一部分所占比重增大,其他部分会相应地减少。二、率用以说明某种现象发生的频率或强度,故又称频率指标,以100,1000,10000或100000为比例基数(K)均可,原则上以结果至少保留一位整数为宜,其计算公式为:率和构成比不同之处:率的大小仅取决于某种现象的发生数和可能发生该现象的总数,不受其他指标的影响,并且各率之和一般不为1。率=×K该式亦可用符号表达如下阳性率=×K(若算阴性率则分子为A(-))式中A(+)为阳性人数,A(-)为阴性人数。三、相对比表示有关事物指标之对比,常以百分数和倍数表示,其公式为:相对比:甲指标/乙指标(或×100%)或用符号表示为:A/B×K四、注意事项①构成比和率的不同,不能以比代率;②计算相对数时,观察例数不宜过小;③率的比较注意可比性,特别是混杂因素的问题,有的话,可用标准化法和分层分析消除;④观察单位不同的几个率的平均率不等于几个率的算术均数;⑤样本率或构成比的比较应做假设检验。第五节分类变量资料的统计推断(非常重要)一、率的抽样误差专业技术资料分享\nWORD文档下载可编辑用抽样方法进行研究时,必然存在抽样误差。率的抽样误差大小可用率的标准误来表示,计算公式如下:σp=式中:σp为率的标准误,π为总体阳性率,n为样本含量。因为实际工作中很难知道总体阳性率π,故一般采用样本率P来代替,而上式就变为Sp=二、总体率的可信区间由于样本率与总体率之间存在着抽样误差,所以也需根据样本率来推算总体率所在的范围,根据样本含量n和样本率P的大小不同,分别采用下列两种方法:(一)正态近似法(常考!)当样本含量n足够大,且样本率P和(1-P)均不太小,如nP或n(1-P)均≥5时,样本率的分布近似正态分布。则总体率的可信区间可由下列公式估计:总体率(π)的95%可信区间:p±1.96sp总体率(π)的99%可信区间:p±2.58sp(二)查表法当样本含量n较小,如n≤50,特别是P接近0或1时,则按二项分布原理确定总体率的可信区间,其计算较繁,读者可根据样本含量n和阳性数x参照专用统计学介绍的二项分布中95%可信限表。三、u检验(非常重要!)当样本含量n足够大,且样本率P和(1-P)均不太小,如nP或n(1-P)均≥5时,样本率的分布近似正态分布。样本率和总体率之间、两个样本率之间差异的判断可用u检验。1.样本率和总体率的比较公式u=|P-π|/σP=|P-π|/;2.两样本率比较公式u=|P1-P2|/Sp1-P2=|P1-P2|/也可用χ2检验,两者相等。四、χ2检验(非常重要!)可用于两个及两个以上率或构成比的比较;两分类变量相关关系分析。其数据构成,一定是相互对立的两组数据,四格表资料自由度v永远=1。四格表χ2检验各种公式适用条件,n>40且每个格子T>5,可用基本公式或专用公式,不用校正。基本公式:χ2=∑(A-T)2/T专用公式:χ2=∑(ad-bc)2n/(a+b)(c+d)(a+c)(b+d)只要有一个格子T在1~5之间,需校正。校正公式:基本公式:χ2=∑(|A-T|-0.5)2/T专用公式:χ2=∑(|ad-bc|-n/2)2n/(a+b)(c+d)(a+c)(b+d)n<40或T<1,用确切概率法。五、行×列表χ2检验当行数或列数超过2时,称为行×列表。行×列表χ2检验是对多个样本率(或构成比)的检验。适用条件:一般认为行×专业技术资料分享\nWORD文档下载可编辑列表中不宜有1/5以上格子的理论数小于5,或有小于1的理论数。1.当理论数太小可采取下列方法处理①增加样本含量以增大理论数;②删去上述理论数太小的行和列;③将太小理论数所在组与性质相近的组合并,使重新计算的理论数增大。由于后两法可能会损失信息,损害样本的随机性,不同的合并方式有可能影响推断结论,故不宜作常规方法。另外,不能把不同性质的实际数合并,如研究血型时,不能把不同的血型资料合并。2.如检验结果拒绝检验假设,只能认为各总体率或总体构成比之间总的来说有差别,但不能说明它们彼此之间都有差别,或某两者间有差别。3.关于单向有序行列表的统计处理在比较各处理组的效应有无差别时,宜用秩和检验法,如作χ2检验只说明各处理组的效应在构成比上有无差异。六、配对计数资料的χ2检验同一样品用两种方法处理,观察阳性和阴性个数。判断两种处理方法是否相同。当b+c>40时,χ2=(b-c)2/b+c;b+c<40时,校正公式:χ2=(|b-c|-1)2/b+c第六节直线相关和回归(一般考点)一、直线相关分析的用途、相关系数及其意义相关分析是研究事物或现象之间有无关系、关系的方向和密切程度。相关系数:是定量表示两个变量(X,Y)之间线性关系的方向和密切程度的指标,用r表示,r=lxy/,其值在-1至+1间,r没有单位。r呈正值,两变量间呈正相关,即两者的变化趋势是同向的,r=1时为完全正相关;如r呈负值,两变量呈负相关,即两者的变化趋势是反向的,r=-1时为完全负相关。r的绝对值越接近1,两变量间线性相关越密切;越接近于0,相关越不密切。当r=0时,说明X和Y两个变量之间无直线关系。二、直线回归分析的作用、回归系数及其意义直线回归分析的任务在于找出两个变量有依存关系的直线方程,以确定一条最接近于各实测点的直线,使各实测点与该线的纵向距离的平方和为最小。这个方程称为直线回归方程,据此方程描绘的直线就是回归直线。直线同归方程式的一般表达式Y=a+bX式中a为回归直线在Y轴上的截距,即a>0表示直线与Y轴的交点在原点上方,<0在原点下方,a=0过原点。b为样本回归系数,即回归直线的斜率,表示当X变动一个单位时,Y平均变动b个单位。b>0:表示Y随X增大而增大b<0:表示Y随X增大而减少b=0:表示Y不随X变化而变化第七节统计表和统计图(重要考点)一、统计表原则:结构简单、层次分明、内容安排合理、重点突出、数据准确。1.标题简练表达表的中心内容,位置在表的上方。2.标目有横标和纵标目,横标目通常位于表内左侧;纵标目列在表内上方,其表达结果与主辞呼应。3.线条力求简洁,一般为三线表。专业技术资料分享\nWORD文档下载可编辑4.用阿拉伯数表示,如无数据或暂缺资料,也可用“-”或“…”来表示。5.备注一般不列入表内,解释在表下。内容排列:一般按事物发生频率大小顺序来排列,对比鲜明,重点突出。二、统计图1.线图(linediagram)(常考!)资料性质:适用于连续变量资料。分析目的:用线段的升降表达某事物的动态(差值)变化。2.半对数线图(semilogarithmiclinegraph)资料性质:适用于连续变量资料。分析目的:用线段的升降表达事物的发展速度变化趋势。3.直方图(histogram)资料性质:适用于数值变量,连续性资料的频数表资料。分析目的:直方图是以直方面积表达各组段的频数或频率。4.直条图(barchart)资料性质:适用于彼此独立的资料。分析目的:直条图是用等宽直条的和长短来表示各统计量的大小,进行比较。5.百分条图(percentchart)资料性质:构成比。分析目的:用长条各段的长度(面积)表达内部构成比。6.圆形图(circulargraph)(常考!)资料性质:构成比。分析目的:用圆的扇形面积表达内部构成比。7.散点图(scatterdiagram)资料性质:双变量资料。分析目的:用点的密集度和趋势表达两变量间的相关关系。8.统计地图(statisticalmap)资料性质:地区性资料。分析目的:用不同纹线或颜色代表指标高低,说明地域分布。专业技术资料分享