- 2022-08-13 发布 |
- 37.5 KB |
- 8页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
统计学文献25
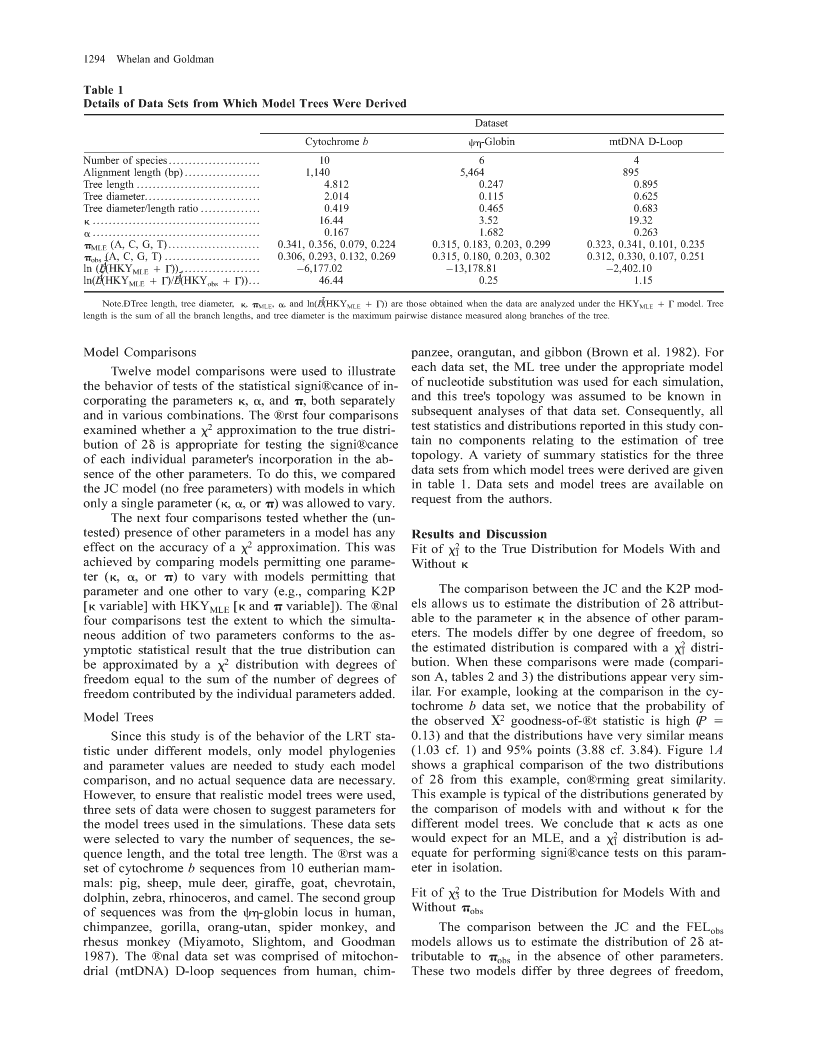
DistributionsofStatisticsUsedfortheComparisonofModelsofSequenceEvolutioninPhylogeneticsSimonWhelanandNickGoldmanDepartmentofGenetics,UniversityofCambridgeAsymptoticstatisticaltheorysuggeststhatwhentwonestedmodelsarecomparedbyalikelihoodratiotest,ax2distribution,withnumberofdegreesoffreedomequaltothedifferenceinnumbersoffreeparametersofthetwomodels,canbeusedforsigni®cancetesting.Thisasymptoticresulthasbeenassumedtoapplyinphylogeneticswiththesupportofonlyafewstudies.Inthispaper,12comparisonsamongaselectionofcommonlyusedmodelsofnucleotidesubstitutionwereexaminedtoseewhetherthisassumptionisreasonable.Thetruedistributionsoflikelihoodratiostatisticswereestimatedbycomputersimulationandcomparedwiththeappropriatex2distributions.Itwasfoundthatx2distributionsareadequateforsigni®cancetestinginthecomparisonofmodelsdifferingbyparametersdescribingtransition/transversionbiasand/orunequalbasefrequencieswhentheseparametershavebeenestimatedbymaximumlikelihood.Thex2distributionwas,however,foundtobesigni®cantlydifferentfromthetruedistributionsinthecomparisonofmodelsdifferingbyparametersdescribingratevariationacrosssites(esti-matedbymaximumlikelihood)orunequalbasefrequencies(estimatedastheobservedbasefrequenciesinanalignment).Theselast®ndingsmayhaveimportantconsequencesforreal-modelcomparisonsandfortheconstruc-tionofincreasinglycomplexandrealisticmodelsofnucleotidesequenceevolution.IntroductionIntheestimationofphylogenyfromhomologousquitestraightforwardandtheresultsareoftenpredict-DNAsequences,itisoftenassumedthateachbasefol-able,butthisisnotnecessarilythecaseforallMarkovlowsaMarkovprocessofnucleotidesubstitution(Swof-modelsinvolvingtheuseofatreestructure.Thisispo-fordetal.1996;LioÁandGoldman1998).Thesubsti-tentiallyveryimportantforthedevelopmentofmoretutionmodelsthatdescribeevolutioninthismannercomplexmodelsforwhichthedifferencesinlikelihoodmakeseveralinherentassumptions:thateachsiteisin-willbefarsmallerandtheexactdistributionsusedfordependentofchangeatallothersites(andtypicallyfol-signi®cancetestingwillbeofgreaterimportance(Yanglowsthesameprocess),thattheMarkovprocessiscon-1998;HuelsenbeckandNielsen1999).Inthisstudy,westantintimeandacrosslineages,andthatbasefrequen-examinethedistributionsofstatisticsusedforsigni®-ciesareatequilibrium.Themostcommonlyusedmod-cancetestinginthecaseofnestedmodelsofnucleotideelsofnucleotidesubstitutiontendtoparameterizethissubstitution.processintorelativelyfewparametersthatareintendedApairofmodelsissaidtobenestedifone(sim-tohavebiologicalmeanings,forexample,representingpler)modelisaspecialcaseoftheother(morecomplex)biasintransition/transversionrates(Kimura1980),un-model;inotherwords,thesimplermodelcanbederivedequalnucleotidefrequencies(Felsenstein1981),orvar-fromthemorecomplexmodelby®xingoneormoreiationinsubstitutionratesamongsites(Yang1993,parameterstospeci®edvalues.Thelikelihoodratiotest1994).(LRT)betweentwonestedmodelscomparesthein-Thesemodelsarethebasisofbothmaximum-like-creaseinlikelihoodobtainedbytheadditionofextralihood(ML)anddistancemethodsofphylogeneticre-parameterstothesimplermodelwiththeincreaseex-construction.However,MListheonlymethodthatper-pectedwhenthesimplermodelisinfactcorrect.As-mitsstatisticaltestingbetweenmodels(Goldman1993;ymptoticstatisticaltheorystatesthatasigni®cancetestHuelsenbeckandRannala1997)andcanthereforebecanbeformulatedusingax2distributionwithanap-usedtoelicitmorethanjustthephylogeneticrelation-propriatenumberofdegreesoffreedom(Wald1949;shipamongthehomologoussequences.Forexample,Silvey1975).Inthepast,ithasbeenwidelyassumedcomparisonsbetweenmodelscanbeusedtoinvestigatethatthisasymptoticstateholdsforthecomparisonofhowtheprocessofevolutionoccursandwhetherselec-modelsofnucleotidesubstitutioninphylogenetics.Fewtionhasoccurredinanyofthelineages(Yang1998).studieshaveattemptedtoseewhetherthisapproxima-MLmethodsarewellsuitedforthesecomparisonsbe-tionisaccurate(butseeYang,Goldman,andFridaycausetheyallowonetoaccuratelytestwhetherthead-1995).Inthisstudy,weexaminethisbyestimatingtheditionofextraparameterswhichdescribemorecomplextruedistributionsofLRTstatisticsbycomputersimu-biologicalphenomenasigni®cantlyimprovethelikeli-lationandcomparingthesesimulateddistributionstothehoodvalueattainedforagivenmodel.Thequestionsx2distributionspredictedbyasymptotictheory.posedbycomparingthesimplersubstitutionmodelsareMaterialsandMethodsKeywords:likelihood-ratiotests,Markovmodels,maximumlike-ModelsandLikelihoodCalculationslihood,modelcomparison,molecularevolution,phylogenetics.ThemodelsusedinthisstudyinvolvesubsetsofAddressforcorrespondenceandreprints:SimonWhelan,Depart-mentofGenetics,UniversityofCambridge,CambridgeCB23EH,thefollowing®vedistinctparameters.The®rstparam-UnitedKingdom.E-mail:s.whelan@gen.cam.ac.uk.eter,k,describestherateoftransitionsubstitutionsrel-ativetothatoftransversionsubstitutions(Kimura1980).Mol.Biol.Evol.16(9):1292±1299.1999q1999bytheSocietyforMolecularBiologyandEvolution.ISSN:0737-4038Thisparameter'svalueisusually.1duetoanexcess1292\nStatisticsofModelComparisonsinPhylogenetics1293oftransitionsubstitutionsovertransversionsinmostbi-compared(Zharkikh1994;HuelsenbeckandRannalaologicalsequencedata.Thesecondparameter,a,isused1997).TheMLscoresunderbothhypotheses(LÃHH,LÃ)01todescribetheamong-sitevariationintherateofnu-arecalculated,andanLRTstatistic2discalculatedfromcleotidesubstitution(Yang1993,1994).Itmodelsthistheformula:bydescribingeachsite'srateasasamplefromagammaLÃdistributionwithameanof1andavarianceof1/a.2d52lnH152(ln(LÃÃ)2ln(L)).(1)12LÃHH10Highvaluesofarepresentlowamountsofratevaria-H0tion,andlowvaluesrepresentlargeamountsofratevar-Thisstatisticisameasureofhowmuchimprove-iation.Foragivendataset,thevaluesofbothkandamenttheadditionoftheextraparametersinthealter-areusuallytakentobethosewhichgivethehighestnativehypothesisgives,anditcanbeusedtocomparelikelihoodandarethereforeMLestimators(MLEs).Thethetwohypotheses.Toperformsuchasigni®cancetest,®nalparameterstogetherdescribeequilibriumbasefre-thedistributionof2dunderH0mustbeknown.quencies(Felsenstein1981).AlthoughtherearefourbasefrequenciespA,pC,pG,andpT,representedhereAsymptotic,True,andEstimatedDistributionsofthebytheparametervectorp,theydescribethreeindepen-LRTStatisticdentparametersbecauseofthenecessitythattheysumTheLRTstatistic2dgivesameasureofhowmuchto1.AlthoughthevaluesoftheseparameterscanalsoimprovementthealternativehypothesisgivesoverthebecalculatedasMLEs(pMLE)foragivendataset,innullhypothesis,andprovidingthetwohypothesesarepracticethevaluesareusuallytakentobethefrequen-nested,2dwillalwaysbenonnegative.Astheadditionciesofthebasesasobservedinthesequences(pobs).ofextraparameterscanonlyimprovetheMLscore,itThe®rstfourmodelsusedinthisstudy®xaequalisimportanttoknowhowlarge2dmustbebeforethetoin®nity,whichmeansthereisnodescriptionofratenullhypothesisisrejectedinfavorofthealternativevariationinthem.The®rstofthese,denotedJC,washypothesis.IftheadditionalparametersinthealternativedevelopedbyJukesandCantor(1969)andisoftenhypothesisarenotsigni®cant,thentheincreasein2dknownastheequiprobablemodel.Itmakestherestric-simplyrepresentstheabilityoftheseparameterstode-tionsthatk51andpA5pC5pG5pT5¼andscribethenoiseofthestochasticprocessthatgeneratedresultsinamodelwhereeachnucleotidesubstitutionisthedata.Adatasetgeneratedbythenullhypothesisequallylikely.Thesecondmodel,K2P(Kimura1980),modelandanalyzedunderthenullandalternativehy-assignsthebasefrequenciesthesamevalue,pA5pCpotheseswillgiveavalueof2ddrawnfromthetrue5pG5pT5¼,whileallowingktovary.Thethirdnullhypothesisdistributionofincrease;thisdistributionmodel,FEL(Felsenstein1981)®xesk51butimposesistheonewhichideallyshouldbeusedforsigni®cancenoconstraintsonp.Thefourthmodel,HKY(Hasega-testing.Statisticaltheoryindicatesthat,asymptotically,wa,Kishino,andYano1985),allowsbothpandkto2d;x2n,wherenisthenumberofdegreesoffreedomvary(kisequivalenttob/ainthenotationofHasegawa,bywhichH0andH1differ.OuraimistoseeifthisKishino,andYano1985).approximationisaccurateforphylogeneticinferenceThenextfourmodels,denotedJC1G,K2P1G,with®nitedatasets.Unfortunately,thetruedistributionFEL1G,andHKY1G,arethesameasthemodelsal-of2dcannotbeobtainedbecauseofthecomplexityofreadydescribedexceptthateachadditionallyallowsfortheMLanalysiswithphylogenetictreesandthuscanamong-siteratevariationbyallowingatovary.Finally,onlybeapproximatedbycomputersimulation.themodelswhichallowptovarycanbeusedintwoThisisdonebysimulatingdataundertheproba-forms:®rst,whenpisestimatedfromtheobservedbasebilisticmodelusedinthenullhypothesiswiththefreefrequencies(modelsdenotedFELobs,HKYobs1G,etc.)parameterssettothevaluesestimatedfromtherealdataandsecond,whenpisestimatedbyitsMLE(modelsset.TheresultantsequencesarethenanalyzedunderdenotedFELMLE,HKYMLE1G,etc.).bothhypotheses,andthestatistic2discalculated.ThisTheMLcalculationsinthisstudywereperformedprocessisrepeatedmanytimes,andtheresultantdistri-usingstandardprocedures(Felsenstein1981;Swoffordbutionof2disaparametricestimateofthetruedistri-etal.1996)andwerecomputedbythelocallywrittenbution.ThisprocedureisexplainedingreaterdetailbyprogramandPAML(Yang1997).GammadistributionsGoldman(1993).Thesimulateddistributionof2diswereimplementedusingthe``discretegamma''approx-comparedwiththepredictedx2distributionbyastan-imation(Yang1994)witheightratecategories.dardgoodness-of-®ttestusingPearson'sx2statistic(Lindgren1976).ItisalsoofinteresttocomparetheLRTStatisticmeansand95%pointsofthesimulatedandpredictedLikelihoodvaluescanbeusedforthestatisticalx2distributions.comparisonoftwomodels.Thisisdoneviathefor-Alldatasimulationswereperformedusingalocallymulationoftwoexplicithypotheses:thenullhypothesiswrittenprogram.Thenumberofrepetitionsperformed(H0)andthealternativehypothesis(H1).Eachoftheiscrucial,astoofewcouldleadtopoorestimatesofthemodelcomparisonsinthisstudyinvolvestwonestedtruedistribution.Inthisstudy,eachmodelcomparisonmodels,whichmeansthatthealternativehypothesisisused1,000repetitions.Henceforth,forbrevity,weab-amorecomplexformofthenullhypothesisrepresentedbreviatetheestimatedtruedistributionoftheLRTsta-bytheadditionofextraparameters.Thisisoftenthetistic2dderivedfromthesesimulationsto``thetruedis-caseinphylogeneticswhenmodelsofevolutionaretribution.''\n1294WhelanandGoldmanTable1DetailsofDataSetsfromWhichModelTreesWereDerivedDatasetCytochromebch-GlobinmtDNAD-LoopNumberofspecies.......................1064Alignmentlength(bp)...................1,1405,464895Treelength...............................4.8120.2470.895Treediameter.............................2.0140.1150.625Treediameter/lengthratio...............0.4190.4650.683k..........................................16.443.5219.32a..........................................0.1671.6820.263pMLE(A,C,G,T).......................0.341,0.356,0.079,0.2240.315,0.183,0.203,0.2990.323,0.341,0.101,0.235pobs(A,C,G,T)........................0.306,0.293,0.132,0.2690.315,0.180,0.203,0.3020.312,0.330,0.107,0.251ln(LÃ(HKYMLE1G))....................26,177.02213,178.8122,402.10ln(LÃ(HKYMLE1G)/LÃ(HKYobs1G))...46.440.251.15Note.ÐTreelength,treediameter,k,pMLE,a,andln(LÃ(HKYMLE1G))arethoseobtainedwhenthedataareanalyzedundertheHKYMLE1Gmodel.Treelengthisthesumofallthebranchlengths,andtreediameteristhemaximumpairwisedistancemeasuredalongbranchesofthetree.ModelComparisonspanzee,orangutan,andgibbon(Brownetal.1982).ForTwelvemodelcomparisonswereusedtoillustrateeachdataset,theMLtreeundertheappropriatemodelthebehavioroftestsofthestatisticalsigni®canceofin-ofnucleotidesubstitutionwasusedforeachsimulation,corporatingtheparametersk,a,andp,bothseparatelyandthistree'stopologywasassumedtobeknowninandinvariouscombinations.The®rstfourcomparisonssubsequentanalysesofthatdataset.Consequently,allexaminedwhetherax2approximationtothetruedistri-teststatisticsanddistributionsreportedinthisstudycon-butionof2disappropriatefortestingthesigni®cancetainnocomponentsrelatingtotheestimationoftreeofeachindividualparameter'sincorporationintheab-topology.Avarietyofsummarystatisticsforthethreesenceoftheotherparameters.Todothis,wecompareddatasetsfromwhichmodeltreeswerederivedaregiventheJCmodel(nofreeparameters)withmodelsinwhichintable1.Datasetsandmodeltreesareavailableononlyasingleparameter(k,a,orp)wasallowedtovary.requestfromtheauthors.Thenextfourcomparisonstestedwhetherthe(un-tested)presenceofotherparametersinamodelhasanyResultsandDiscussioneffectontheaccuracyofax2approximation.ThiswasFitofx2totheTrueDistributionforModelsWithand1achievedbycomparingmodelspermittingoneparame-Withoutkter(k,a,orp)tovarywithmodelspermittingthatparameterandoneothertovary(e.g.,comparingK2PThecomparisonbetweentheJCandtheK2Pmod-[kvariable]withHKYMLE[kandpvariable]).The®nalelsallowsustoestimatethedistributionof2dattribut-fourcomparisonstesttheextenttowhichthesimulta-abletotheparameterkintheabsenceofotherparam-neousadditionoftwoparametersconformstotheas-eters.Themodelsdifferbyonedegreeoffreedom,soymptoticstatisticalresultthatthetruedistributioncantheestimateddistributioniscomparedwithax21distri-beapproximatedbyax2distributionwithdegreesofbution.Whenthesecomparisonsweremade(compari-freedomequaltothesumofthenumberofdegreesofsonA,tables2and3)thedistributionsappearverysim-freedomcontributedbytheindividualparametersadded.ilar.Forexample,lookingatthecomparisoninthecy-tochromebdataset,wenoticethattheprobabilityofModelTreestheobservedX2goodness-of-®tstatisticishigh(P5SincethisstudyisofthebehavioroftheLRTsta-0.13)andthatthedistributionshaveverysimilarmeanstisticunderdifferentmodels,onlymodelphylogenies(1.03cf.1)and95%points(3.88cf.3.84).Figure1Aandparametervaluesareneededtostudyeachmodelshowsagraphicalcomparisonofthetwodistributionscomparison,andnoactualsequencedataarenecessary.of2dfromthisexample,con®rminggreatsimilarity.However,toensurethatrealisticmodeltreeswereused,Thisexampleistypicalofthedistributionsgeneratedbythreesetsofdatawerechosentosuggestparametersforthecomparisonofmodelswithandwithoutkforthethemodeltreesusedinthesimulations.Thesedatasetsdifferentmodeltrees.Weconcludethatkactsasonewereselectedtovarythenumberofsequences,these-wouldexpectforanMLE,andax21distributionisad-quencelength,andthetotaltreelength.The®rstwasaequateforperformingsigni®cancetestsonthisparam-setofcytochromebsequencesfrom10eutherianmam-eterinisolation.mals:pig,sheep,muledeer,giraffe,goat,chevrotain,Fitofx23totheTrueDistributionforModelsWithanddolphin,zebra,rhinoceros,andcamel.Thesecondgroupofsequenceswasfromthech-globinlocusinhuman,Withoutpobschimpanzee,gorilla,orang-utan,spidermonkey,andThecomparisonbetweentheJCandtheFELobsrhesusmonkey(Miyamoto,Slightom,andGoodmanmodelsallowsustoestimatethedistributionof2dat-1987).The®naldatasetwascomprisedofmitochon-tributabletopobsintheabsenceofotherparameters.drial(mtDNA)D-loopsequencesfromhuman,chim-Thesetwomodelsdifferbythreedegreesoffreedom,\nStatisticsofModelComparisonsinPhylogenetics1295Table2ProbabilitiesandOtherInformationRelatingtotheFitofPredictedx2DistributionstoEstimatesoftheTrueDistributionof2dModelTreeCytochromebch-GlobinmtDNAD-LoopExtraParametersComparison(dfa)ModelscomparedX2nPX2nPX2nPA......................k(1)JCvs.K2P17.5130.1315.2150.3717.3130.14B......................pobs(3)JCvs.FELobs1,94719,0.00195.420,0.00120020,0.001C......................pMLE(3)JCvs.FELMLE23.6220.3133.4250.1018.8220.61D......................a(1)JCvs.JC1G34811,0.00122811,0.00128411,0.001E......................k(1)FELobsvs.HKYobs12.5140.4911.8130.4710.8120.46F......................pobs(3)JC1Gvs.FELobs1G1,94619,0.00115921,0.0016819,0.001G......................pMLE(3)K2Pvs.HKYMLE7.96210.9922.83210.3016.45230.79H......................a(1)FELMLEvs.FELMLE1G30210,0.00136.3610,0.00158.7410,0.001J.......................k1pMLE(4)JC1Gvs.HKYMLE1G25.3240.3328.6250.2428.3260.29K......................k1pobs(4)JCvs.HKYobs2,95023,0.00110522,0.00113124,0.001L......................k1a(2)FELobsvs.HKYobs1G29715,0.00122617,0.00122015,0.001M.....................a1pobs(4)K2Pvs.HKYobs1G1,89921,0.00130225,0.00113322,0.001Note.ÐX2istheteststatisticforPearson'sx2testofgoodnessof®tbetweenthepredictedx2distributionandtheestimatedtruedistributionof2d;nisthenumberofdegreesoffreedomforthistest.X2iscomparedwithax2ndistributiontoderivethegivenprobabilityP.aDegreesoffreedompredictedbycountingindependentparameters.andstatisticaltheorysuggeststhatiftheseestimatesactreasonforthisisthatthemethodofestimatingpdi-equivalentlytotheMLEsofthebasefrequencies,thenrectlyfromtheobservedbasefrequenciesisevidentlythedistributionof2dwillbeapproximatelyx23.How-notveryaccurateandcanevengiveworse(i.e.,lowerever,whencomparingthisdistributiontoourestimateslikelihood)estimatesthanthenullhypothesisvaluesofofthetruedistribution(comparisonB,tables2and3)equalbasefrequencies.Thetwomodelsarenotstrictlyitisevidentthattheyaredifferent.Thisisillustratedbynestedbecauseforagivendataset,theFELobsmodellookingatthiscomparisoninthech-globindataset.cannotuseallpossiblevaluesofp.Ithasbeenpre-Thepredictedx23andtheestimateofthetruedistributionsumedthattheobservedbasefrequenciesarereasonableforthiscomparisonarealsoshownin®gure1B.TheapproximationsoftheMLEfrequencies,atleastforlonggoodness-of-®ttestshowsthattheyareclearlydifferentsequences,buttheseresultsshowthatthisisnotalways(P,0.001;comparisonBintable2),andthisiscon-thecase.Thisisfurtherillustratedbythedifferences®rmedbythedifferenceinthemeansandthe95%betweenpobsandpMLEandthevaluesofln(LÃ(HKYMLEpointsofthetwodistributions(comparisonB,table3).1G)/LÃ(HKYobs1G))reportedintable1Ðseeinpar-Differencesinthe95%pointmaybemostcrucial,asticularthecytochromebdataset.thisvalueistheonetypicallychosentodelimitsignif-Fitofx2totheTrueDistributionforModelsWithand3icanttestresultsfromnonsigni®canttestresults.TheWithoutpMLEmoststrikingdifferencebetweenthetwodistributionsisThecomparisonbetweentheJCandFELMLEmod-thatthesimulateddistributionhasnegativevalues.Theelsallowsustoestimatethetruedistributionof2dat-Table3PropertiesofEstimatedTrueDistributionsof2dinRelationtothePredictedx2DistributionsModelTreeCytochromebch-GlobinmtDNAD-LoopPredictedx2ExtraParametersComparison(dfa)ModelscomparedMean95%Mean95%Mean95%Mean95%A..................k(1)JCvs.K2P1.033.880.964.040.993.981.003.84B..................pobs(3)JCvs.FELobs1.366.842.617.162.627.393.007.81C..................pMLE(3)JCvs.FELMLE2.927.933.248.522.937.823.007.81D..................a(1)JCvs.JC1G0.292.640.472.690.492.921.003.84E..................k(1)FELobsvs.HKYobs1.013.861.024.230.973.751.003.84F..................pobs(3)JC1Gvs.FELobs1G1.856.842.557.302.637.483.007.81G..................pMLE(3)K2Pvs.HKYMLE2.978.043.007.933.057.783.007.81H..................a(1)FELMLEvs.FELMLE1G0.282.590.723.230.732.911.003.84J..................k1pMLE(4)JC1Gvs.HKYMLE1G4.109.513.438.664.009.414.009.49K..................k1pobs(4)JCvs.HKYobs2.378.083.638.813.698.824.009.49L..................k1a(2)FELobsvs.HKYobs1G1.294.711.435.001.394.972.005.99M.................a1pobs(4)K2Pvs.HKYobs1G1.877.543.248.953.028.734.009.49Note.ÐForeachmodeltree,themeanand95%pointoftheestimatedtruedistributionof2disshown.Thecorrespondingpointsofthex2distributionwithdegreesoffreedompredictedbythenumberofextraparametersinthemorecomplexmodelarealsogiven.aDegreesoffreedompredictedbycountingindependentparameters.\n1296WhelanandGoldmantributabletothepMLEparametersintheabsenceofotherparameters.Ax23distributionwascomparedwiththeestimateofthetruedistributionandwasfoundtobeverysimilar.Forexample,considerthecomparisonofJCandFELinthech-globindataset(comparisonC,tables2and3).Acomparisonofthesimulateddistri-butionandthex2distributionisshownin®gure1C,anditisclearthattheyareverysimilar(P50.10),withthesimulateddistributionhavingameanof3.24andthex2distributionhavingameanof3.Thissuggeststhatwhentheparameterpisestimatedbythismethod,itactsasonewouldexpectanMLEto.Thiswastrueinallcom-parisonsoftheJCandFELMLEmodels.Weconcludethatthex23distributionisadequateforsigni®cancetestsinthiscase.Fitofx21totheTrueDistributionforModelsWithandWithoutaThecomparisonbetweentheJCandJC1Gmodelsallowsustoestimatethedistributionof2dattributabletotheparameteraintheabsenceofotherparameters.Thesetwomodelsdifferbyonedegreeoffreedom,andstatisticaltheorypredictsthat2dshouldbeasymptoti-callydistributedasx21.Whencomparingthisdistributionwithourestimatesofthetruedistribution,itisevidentthatthetwoaredifferent.Thisisillustratedbytakingonespeci®cexamplefromthoseshownintables2and3,thecomparisonoftheJCandJC1GmodelsforthemtDNAD-loopdataset(comparisonD).Agraphicalcomparisonofthetruedistributionandthepredictedx2distributionisshownin®gure1D,withtheestimateofthetruedistributionbeingclearlydifferentfromthepre-dictedx2distributionandappearingtobeskewedtotheleft.Thegoodness-of-®ttestcomparingthetwodistri-butionscon®rmsthatitisveryunlikelythatthetwodistributionsarethesame(P,0.001;comparisonDintable2),andthemeansandthe95%pointsforthetwodistributionsclearlydiffer(comparisonD,table3).Thismeansthattheaparameterinthegammadistributiondoesnotinducetheexpecteddistributionfor2d.Thisresultistypicalofallthecomparisonsperformedbe-tweenmodelswithandwithoutthegammadistribution.Webelievethisresultoccursbecausetheparametervalueforwhichthemorecomplexmodelreducestothesimplermodel,a5`,liesontheboundaryofthesetofpermittedvalues(0,`).Insuchcases,theasymptoticstatisticaltheorypredictingax2distributionfor2dis¬FIG.1.ÐGraphicalcomparisonsoftheestimatedtruedistributions(whitebars)andtheappropriatepredictedx2distributions(blackbars)foravarietyofmodelcomparisons.A,ComparisonbetweentheJCandK2Pmodelsusingthecytochromebmodeltree(predicteddistri-butionx21notsigni®cantlydifferentfromtruedistribution,P50.13).B,ComparisonbetweentheJCandFELobsmodelsusingthech-globinmodeltree(predicteddistributionx23signi®cantlydifferentfromtruedistribution,P,0.001).C,ComparisonbetweentheJCandFELMLEmodelsusingthech-globinmodeltree(predicteddistributionx23notsigni®cantlydifferentfromtruedistribution,P50.10).D,ComparisonbetweentheJCandJC1GmodelsusingthemtDNAD-loopmodeltree(predicteddistributionx21signi®cantlydifferentfromtruedistri-bution,P,0.001).\nStatisticsofModelComparisonsinPhylogenetics1297notapplicable.Instead,itispossiblethattheasymptoticFELobs1G;comparisonsFandH,respectively,intablesdistributionof2dwillbexÅ2,whichrepresentsamixture2and3)eachbehavedasbeforeandproducedatrueoftwoormorex2distributions(SelfandLiang1987).distributionthatcouldnotbeapproximatedbyax2dis-ForthecomparisonoftheJCandJC1Gmodels,thetribution.Fromthisweconcludethatthebehaviorofthedistributionof2dwouldbepredictedtobea50:50mix-truedistributionof2dremainsapproximatelyconstanttureofax20distribution(i.e.,adistributiontakingvaluewhentestingforthesigni®canceofaparameter,regard-0withprobability1)andax21distribution.Thismixturelessoftheotherparametersassumedtobepresentindistributionhasameanof0.5anda95%pointof2.71,boththenullandalternativehypothesismodels.andtheJCversusJC1Gcomparisonsintable3(com-TheEffectofCombinationsofParametersontheTrueparisonD)appeartobeinreasonableagreementwithDistributionthis.Thegoodness-of-®ttestcomparingthetrueandpredictedmixturedistributionsforthemtDNAD-loopAccordingtostatisticaltheory,thedistributionofdatasetcon®rmsthisgoodagreement(P50.48;details2dinacomparisonoftwonestedmodelsvaryingbynotshown).TheapplicabilityofxÅ2distributionsforsig-multipleparameterswillbeasymptoticallyx2withde-ni®cancetestingofotherphylogenetichypothesesisstillgreesoffreedomequaltothesumofthedegreesofunderinvestigation.Thissituationdoesnotariseforthefreedomcontributedbythevariousparameters.Fourotherparametersstudiedinthispaper(k51cf.per-modelcomparisonswerechosentotestthisassumptionmittedinterval[0,`);pA5pC5G5pT5¼cf.inthephylogeneticcontextofmodelsofnucleotidesub-permittedintervals[0,1]foreachpX,subjecttotheirstitution.The®rstcomparison,JC1Gvs.HKYMLE1G,sumbeing1).involvedtheadditionoftwoparameters(k,pMLE)thatOften,thediscrepancybetweenthetruedistributioneachgavethepredictedx2distributionsfor2dwhenandthepredictedx2distributionwillnotbeamajortestedindividually.Theresultsintables2and3(com-issueintheapplicationofthegammadistributiontorealparisonJ)con®rmthat2ddoesindeedhaveadistribu-phylogeneticdata.Theincreaseinlikelihoodobtainedtionwhichisnotsigni®cantlydifferentfromthepre-byaddingthegammadistributiontoamodelisgener-dictedx24.Forexample,inthecytochromebdataset,allymuchhigherthanthe95%pointofeitherthesim-themeansare4.10and4andthe95%pointsare9.51ulateddistributionorthex21distribution.However,inaand9.49,andthegoodness-of-®ttestindicatesnosig-widercontext,theobservationthatthisMLEdoesnotni®cantdifference(P50.33).actasonewouldexpectmaybecomeimportantwhenThe®nalthreemodelcomparisonsallincludedattestingmorecomplexmodelsforwhichthehypothesisleastoneparameterthatinducedadistributionfor2dtestisfortheadditionofasingleparameterandthethatcouldnotbeapproximatedbyax2distribution.increaseinlikelihoodmaybealotsmaller.Whencom-ThesecomparisonswereJCvs.HKYobs,FELobsvs.paringmodelsdifferingbyoneormoreparametersthatHKYobs1GandK2Pvs.HKYobs1G(comparisonsK±M,havenotbeenshowntoactastheasymptoticstatisticaltables2and3).Inallcases,aswouldbeexpected,thetheorywouldsuggest,onecannotbesurewhetherax2induceddistributionsof2dstillcouldnotbewellap-approximationwillbeappropriateforsigni®cancetest-proximatedbythepredictedx2distributions.Theresultsing.Usinganincorrectapproximationofthetruedistri-intables2and3(comparisonsK±M)forthesemodelbutioncouldleadtoincorrectconclusionsbeingdrawncomparisonscon®rmthis.AllhaveP,0.001forthefromthesigni®cancetest.goodness-of-®ttestsbetweenthetrueandx2distribu-tions,andthemeansand95%pointsalsovaryconsid-TheEffectofthePresenceofOtherParametersontheerably.TrueDistributionEffectofTreePropertiesontheTrueDistributionFourmodelcomparisonsforwhichthenestedpairofmodelsvariedbyasingleparameterwereexaminedThestatisticalcomparisonsofthethreemodeltoseewhethertheconstant(anduntested)presenceoftreesshowthattheparameterskandpMLEinducetheotherparametersaffectstheconclusionsfromtheabovepredictedx2distributionsonthe2dstatistic.Thisresultanalyses.Thefourmodelpairswerechosensothateachseemsindependentofthemodeltreeused.Fortheoth-comparisoninvolvedtheadditionofadifferentparam-ertwoparameters,aandpobs,theredoappeartobeeterandthe``ever-present''parameterwasdifferentindifferencesamongthemodeltreesbetweenthetrueeachcomparison.Theresults(comparisonsE±H,tablesdistributionsof2d.Itisdif®culttorelatethosediffer-2and3)areverysimilartothoseofthepreviousfourencestothepropertiesofthemodeltrees(table1)comparisons.TheadditionofeitherkorpMLE(testsofwithoutfurtherinvestigation.However,somediffer-FELobsvs.HKYobsandK2Pvs.HKYMLE,respectively)encesseemtoberelatedtotreelength.Whencompar-producedestimatesofthetruedistributionthat®ttedtheingmodelswithpMLEandpobs,thereappearstobeappropriatex2distributionsverywell(comparisonsEsomerelationbetweentreelengthandtheaccuracyofandG,tables2and3).This®toccurredevenwhenthepobsasanestimateofpMLE.Thisisshownbycom-ever-presentparameterwasonewhichdidnotitselfin-parisonofthetworelativelyshorttreesderivedfromducethepredicteddistributionfor2d,(e.g.,pobsinthethech-globinandmtDNAD-loopsequencesandthecomparisonFELobsvs.HKYobs).relativelylongtreederivedfromthecytochromebse-Thetwocomparisonswhichinvolvedadditionofquences.Intable1,differencesbetweenpobsandpMLEeitherpobsora(JC1Gvs.FELobs1GandFELobsvs.arefarlowerfortheshortertrees,andtheimprovement\n1298WhelanandGoldmaninln(LÃ)gainedbyusingtheMLEofpisalsolower.roneouslyrejectedinfavorofasimplermodelwithnoTable2showsthattheshorttreeshavefarlower,albeitamong-siteratevariation.Atthistime,thereappearstostillhighlysigni®cant,X2values,suggestinggreaterbenoalternativetotime-consumingdatasimulation(althoughstilllow)similaritybetweenthepredictedx2andreanalysistoaccuratelyestimatethetruedistribu-distributionandthetruedistribution.Table3showstionoftheLRTstatistic2d.Furtherinvestigationsofthatthemeansand95%pointsofthetruedistributionsthepotentialutilityofxÅ2distributionsarecurrentlyun-of2dfortheshorttreesareclosertothecorrespondingderway.pointsofthex23distributionthanarethoseforthelongWhenthex2approximationwasadequate,itwastree.Thisisprobablybecausetherelativelyshortdis-observedthatvariationsinthetreeandthepresenceoftancesofsimulatedevolutionbetweentheobservedse-other(untested)parametersdidnotaffectthis.Thisim-quencesmeanthatthesimilaritiesofindividualse-pliesthataparameterneedonlybeshowntobe``wellquences'basefrequenciesaregoingtobegreater,andbehaved''onceforsubsequentstatisticaltestingbasedthereforepobsisunlikelytobefarfromtheoptimalonpredictedx2distributionstobevalid.ItwasalsopMLE.Theaparameterofthegammadistributionobservedthatwhentwoparametersareaddedsimulta-showsasimilarpatternofbehavior,butthereasonforneously,thedistributiontheyinducefor2disasymp-thecloser®tintheshortertreesisnotcleartousintoticallyx2,withdegreesoffreedomequaltothesumthiscase.ofthedegreesoffreedomcontributedbythevariousparameters,providingeachparameterinducesadistri-butionof2dwhichwasadequatelydescribedbyax2Conclusionsdistributionwhenaddedseparately.ThisiswhatoneTheresultsinthispapershowthatwhennestedwouldexpectfromstatisticaltheory.modelsofnucleotideevolutionarecomparedbylikeli-hoodratiotesting,thetruedistributionof2disnotnec-Acknowledgmentsessarilywellapproximatedbyax2distribution.WhenS.W.issupportedbyaBBSRCResearchStudent-comparingmodelswithandwithoutaparameterde-ship.N.G.issupportedbyaWellcomeTrustFellowshipscribingtransition/transversionbiasorunequalbasefre-2inBiodiversityResearch.WethankRasmusNielsenandquencies,thexapproximationisadequateforstatisticalananonymousrefereeforcommentsregardingestimatestesting,providingtheparametervaluesareestimatedbyofatendingtotheboundaryat`.ML.ThisisnottruewhencomparingmodelswithandwithoutunequalbasefrequenciesestimatedasthebaseLITERATURECITEDfrequenciesobservedinthealignment,ormodelswithandwithoutaparameterdescribingratevariationacrossBROWN,W.M.,E.M.PRAGER,A.WANG,andA.C.WILSON.sites(evenwhenitisestimatedbyML).1982.MitochondrialDNAsequencesofprimates:tempoThe®rstoftheseobservationsisnotsurprisingbe-andmodeofevolution.J.Mol.Evol.18:225±239.causetheapproximationofx2isonlyappropriateforFELSENSTEIN,J.1981.EvolutionarytreesfromDNAsequenc-es:amaximumlikelihoodapproach.J.Mol.Evol.17:368±parametersestimatedbyML.Theresultspresentedhere376.showthatestimatesofthebasefrequenciesobtainedGOLDMAN,N.1993.StatisticaltestsofmodelsofDNAsub-fromthefrequenciesobservedinthealignmentarenotstitution.J.Mol.Evol.36:182±198.necessarilyanaccurateapproximationoftheMLesti-HASEGAWA,M.,H.KISHINO,andT.YANO.1985.Datingofmatesofthesefrequencies.Estimatingthebasefrequen-thehuman-apesplittingbyamolecularclockofmitochon-ciesbyMLsolvesthisproblem.drialDNA.J.Mol.Evol.22:160±174.ThediscrepancybetweenthetruedistributionofHUELSENBECK,J.P.,andR.NIELSEN.1999.Variationinthe2dinducedbytheparameterdescribingratevariationpatternofnucleotidesubstitutionacrosssites.J.Mol.Evol.anditspredictedx2distributionapproximationismore48:86±93.serious.ForcomparisonsinvolvingthemodelsusedinHUELSENBECK,J.P.,andB.RANNALA.1997.Phylogeneticmethodscomeofage:testinghypothesesinanevolutionarythispaperandappliedtorealdata,thisisnotamajorcontext.Science276:227±232.concernbecausethevaluesof2dareusuallyalothigh-JUKES,T.H.,andC.R.CANTOR.1969.Evolutionofproteinerthanthevaluesusedforsigni®cancetestingforbothmolecules.Pp.21±132inH.N.MUNRO,ed.Mammaliandistributions.However,thisresultmayhaveimportantproteinmetabolism.Vol.3.AcademicPress,NewYork.implicationsintheuseofmodelcomparisonstocon-KIMURA,M.1980.Asimplemethodforestimatingevolution-structmorecomplexandrealisticmodelsofnucleotidearyratesofbasesubstitutionsthroughcomparativestudiessequenceevolution.Thevaluesof2dinthesecompar-ofnucleotidesequences.J.Mol.Evol.16:111±120.isonstendtobefarlower(e.g.,Yang1998;Huelsen-LINDGREN,B.W.1976.Statisticaltheory.3rdedition.Mac-beckandNielsen1999)andthecriticalvaluesusedformillan,NewYork.signi®cancetestsareofgreaterimportance.TheuseofLIOÁ,P.,andN.GOLDMAN.1998.Modelsofmolecularevolutionandphylogeny.GenomeRes.8:1233±1244.incorrectdistributionsforstatisticaltestingintheseMIYAMOTO,M.M.,J.L.SLIGHTOM,andM.GOODMAN.1987.casesmayleadtoerroneousconclusionsbeingdrawnPhylogeneticrelationsofhumansandAfricanapesfromfromtheirresults.Forexample,theresultsdescribedDNAsequencesinthech-globinregion.Science238:369±aboveindicatethatcasesmayariseintheanalysisof373.realdatasetsinwhichamodelusingagammadistri-SELF,S.G.,andK.-L.LIANG.1987.Asymptoticpropertiesofbutiontomodelamong-siteratevariationmaybeer-maximumlikelihoodestimatorsandlikelihoodratiotests\nStatisticsofModelComparisonsinPhylogenetics1299undernonstandardconditions.J.Am.Stat.Assoc.82:605±.1997.PAML:aprogrampackageforphylogenetic610.analysisbymaximumlikelihood.CABIOS13:555±556.SILVEY,S.D.1975.Statisticalinference.ChapmanandHall,.1998.Likelihoodratiotestsfordetectingpositivese-London.lectionandapplicationtoprimatelysozymeevolution.Mol.SWOFFORD,D.L.,G.J.OLSEN,P.J.WADDELL,andD.M.Biol.Evol.15:568±573.HILLIS.1996.Phylogeneticinference.Pp.407±514inD.M.YANG,Z.,N.GOLDMAN,andA.FRIDAY.1995.Maximumlike-HILLIS,C.MORITZ,andB.K.MABLE,eds.Molecularsys-lihoodtreesfromDNAsequences:apeculiarstatisticales-tematics.2ndedition.Sinauer,Sunderland,Mass.timationproblem.Syst.Biol.44:384±399.WALD,A.1949.Noteontheconsistencyofthemaximumlike-ZHARKIKH,A.1994.Estimationofevolutionarydistancesbe-lihoodestimate.Ann.Math.Stat.20:595±601.tweennucleotidesequences.J.Mol.Evol.39:315±329.YANG,Z.1993.Maximum-likelihoodestimationofphylogenyfromDNAsequenceswhensubstitutionratesdifferoversites.Mol.Biol.Evol.10:1396±1401.WILLIAMMARTIN,reviewingeditor.1994.MaximumlikelihoodphylogeneticestimationfromDNAsequenceswithvariableratesoversites:ap-proximatemethods.J.Mol.Evol.39:306±314.AcceptedJune3,1999查看更多