- 2022-08-13 发布 |
- 37.5 KB |
- 11页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
心理统计学难点
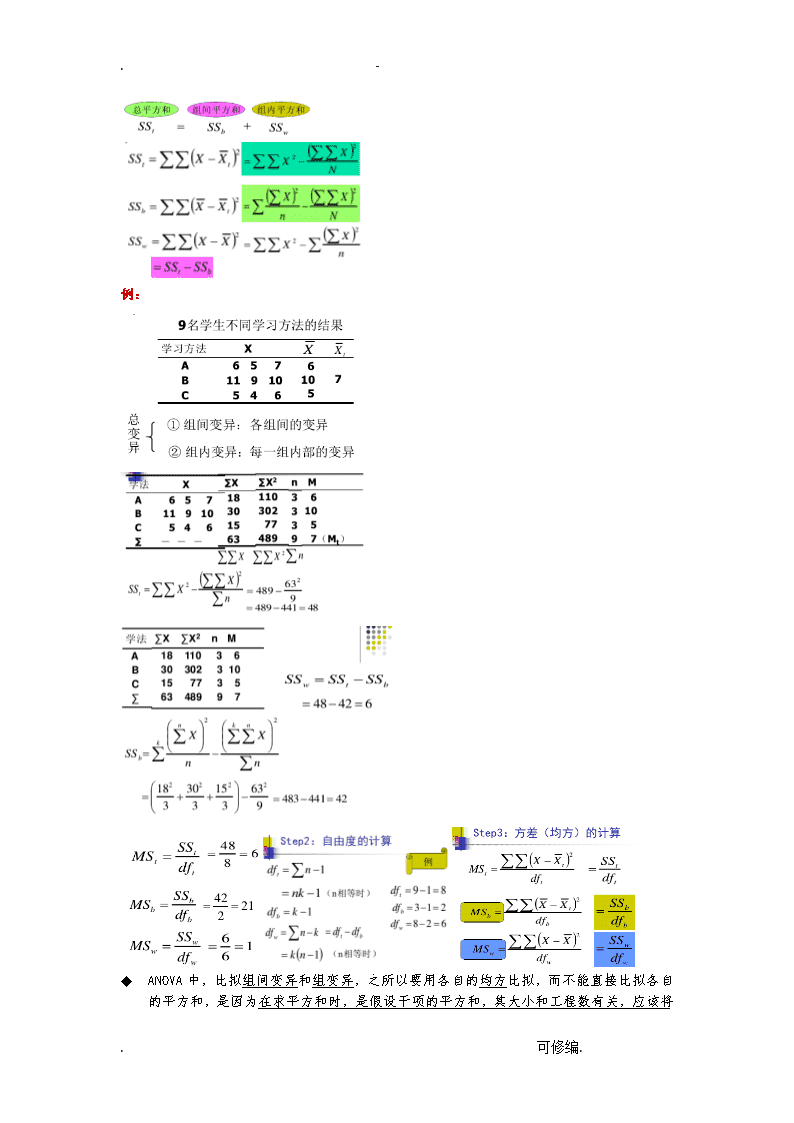
.-例:uANOVA中,比拟组间变异和组变异,之所以要用各自的均方比拟,而不能直接比拟各自的平方和,是因为.可修编.\n.-在求平方和时,是假设干项的平方和,其大小和工程数有关,应该将项数去掉,求其均方才能比拟。因此要除以各自的自由度,求均方。.可修编.\n.-第二节方差齐性检验²方差齐性并不是指方差绝对、完全相等,而仅仅是“相对的〞相等——无统计学差异。即用通过方差齐性检验,各个方差无显著差异。²第三节单因素完全随机设计的方差分析一、实验设计.可修编.\n.-(2)单因素设计类型:①完全随机设计②随机区组设计③拉丁方设计²实验设计专有名词A.实验单位:产生实验结果的被试B.实验因素(因子):实验者所操控的变量〔自变量〕C.水平:实验者在因素所安排的各种不同状况D.处理:不同因子间各水平的组合E.单因素实验:水平与处理意义一样F.效应:实验者在实验单位上所测得的结果〔因变量〕?请举例说明:①.实验因素(因子):实验者所操控的变量〔自变量〕②.水平:实验者在因素所安排的各种不同状况③.处理:不同因子间各水平的组合④.单因素实验:水平与处理意义一样⑤.效应:实验者在实验单位上所测得的结果〔因变量〕二、单因素完全随机设计的方差分析Ø定义:每一随机组分别承受一种实验处理的设计。又名:独立组设计或被试间设计例:随机抽取22名学生并随机为三组,分别做某一种光强〔I、II、III.可修编.\n.-〕的反响时实验。结果如下。试问不同强度的光反响时有无显著不同?第三节单因素随机区组设计的方差分析.可修编.\n.-.可修编.\n.-第四节多因素完全随机设计的方差分析一、两因素完全随机实验设计的方差分析a)题目:主题熟悉性〔A〕与生字密〔B〕度对儿童阅读理解的影响。b)实验变量:自变量A——文章类型,即熟悉的〔a1〕与不熟悉的〔a2〕;c)自变量B——生字密度,即5:1(b1)、10:1(b2)、15:1(b3)d)实验设计:两因素完全随机实验设计e)被试:24名五年级学生f)实验程序:共计2×3=6个实验处理;然后把选取的被试分成6组,每组4人,分别承受一种实验处理水平的结合。二、主效应与交互效应〔一〕主效应〔maineffect〕是指在多因素实验中,只考虑某一变量单独变化所引起观测变量的变化。〔二〕交互效应〔interacteffect〕,也称交互作用,是指一个变量的效应在另一个〔或多个〕自变量的不同水平上是不同的。²交互作用:可能会觉得难于理解统计上的交互作用……但实际上,当开场设计心理学实验的时候,我们很自然的会意识到自变量间存在交互作用的可能性。也就是说,担忧自己关注的变量的效应会由于其他变量的出现而被改变——加强、减弱或消失。这就是交互作用能告诉我们的——一个自变量的效应在另一个自变量的不同水平上是不同的——加强、减弱或消失。Ø主效应与交互效应的关联性在多因素的方差分析中:如果方差分析结果说明交互作用不显著,检验各个因素的主效应就很重要;如交互作用显著,那么对每个因素主效应的检验,意义就不大了。因为交互作用显著,那么意味着两个〔或多个〕因素对实验结果具有共同的重要性。.可修编.\n.-〔这个太难,不强求〕:我们不仅关心听音乐是否对驾驶成绩有影响,还想知道它是否对饮酒者的影响更大。设计一个实验,同时操纵两个变量〔自变量〕:A〔音乐〕×B〔酒精〕完全随机设计下页继续.可修编.\n.-.可修编.\n.-例题:〔考过两次〕教育之通病是教用脑的人不用手,不教用手的人用脑,所以一无所能。教育革命的对策是手脑联盟,结果是手与脑的力量都可以大到不可思议。.可修编.\n.-.可修编.查看更多