统计学上机实验

统计学上机实验

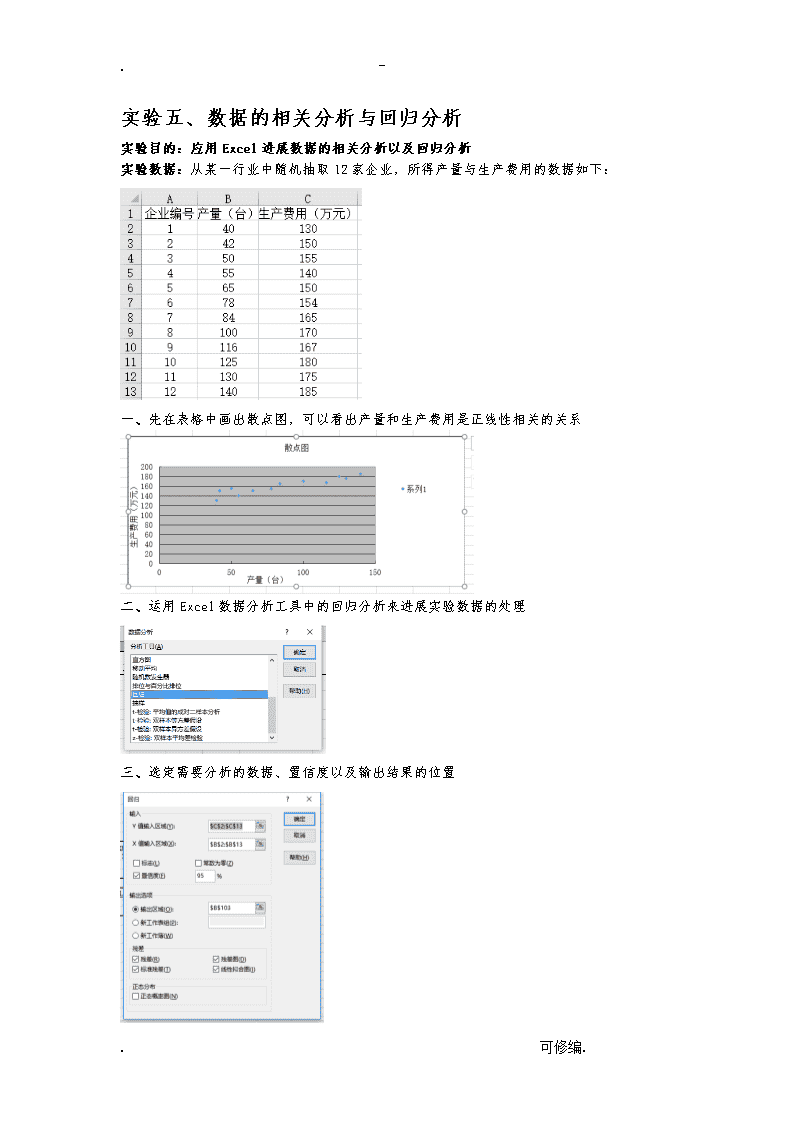
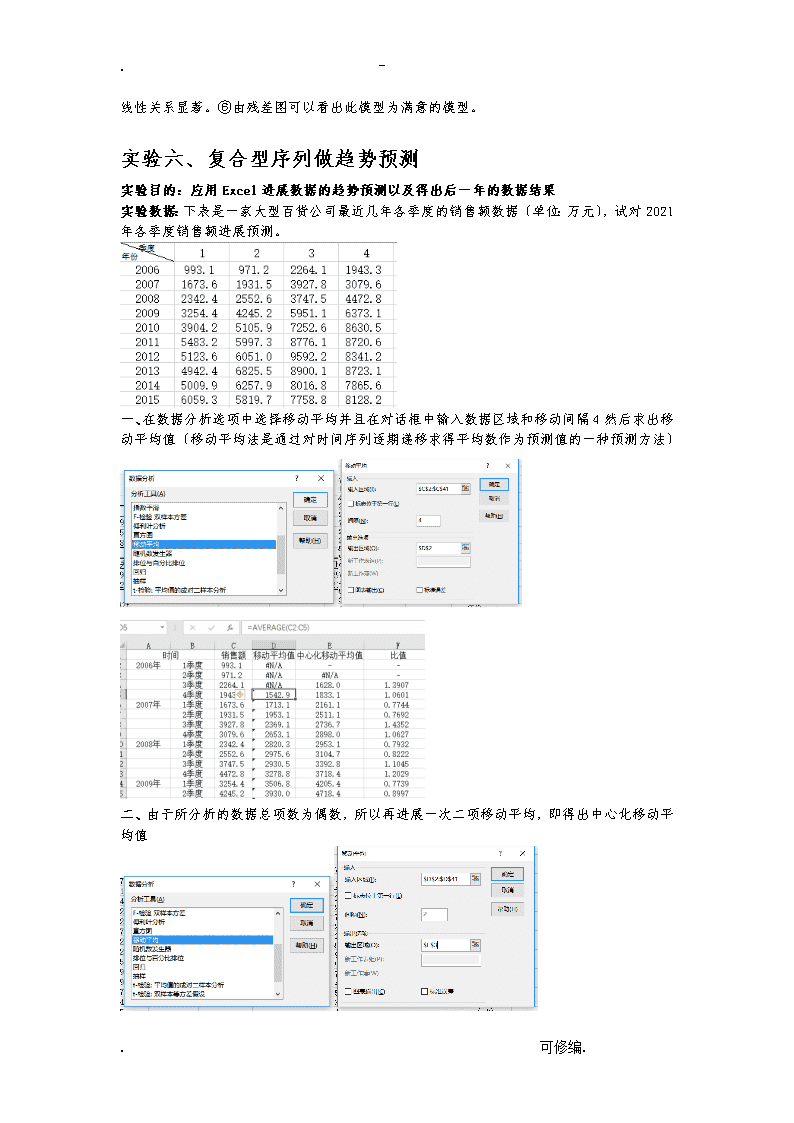
.-实验五、数据的相关分析与回归分析实验目的：应用Excel进展数据的相关分析以及回归分析实验数据：从某一行业中随机抽取12家企业，所得产量与生产费用的数据如下：一、先在表格中画出散点图，可以看出产量和生产费用是正线性相关的关系二、运用Excel数据分析工具中的回归分析来进展实验数据的处理三、选定需要分析的数据、置信度以及输出结果的位置.可修编.\n.-四、输出数据残差图线性拟合图五、分析数据得出实验结论①由得出的实验数据可以得到回归方程：Y=124.14998+0.42068x，由回归方程可以得知产量每增加1台，生产费用平均增加0.42068万元，由线性拟合图可以看出预测值与实际值相差较小。②由相关系数MultipleR可以看出产量与生产费用两者高度线性正相关，并且线性拟合度较高。③由判定系数R²=0.8468=84.68％可以了解到在生产费用的取值变动中有84.68％是由产量决定的，由此可见二者之间有较强的线性关系。④标准误差，那么根据产量来估计生产费用时，平均的估计误差为6.7617万元。⑤计算出的检验统计量F=55.286，根据显著性水平α=0.05，分子自由度和分母的自由度，查F分布表，找到对应的临界值，由于F>.可修编.\n.-，那么回归方程线性关系显著。⑥由残差图可以看出此模型为满意的模型。实验六、复合型序列做趋势预测实验目的：应用Excel进展数据的趋势预测以及得出后一年的数据结果实验数据：下表是一家大型百货公司最近几年各季度的销售额数据〔单位：万元〕，试对2021年各季度销售额进展预测。一、在数据分析选项中选择移动平均并且在对话框中输入数据区域和移动间隔4然后求出移动平均值〔移动平均法是通过对时间序列逐期递移求得平均数作为预测值的一种预测方法〕二、由于所分析的数据总项数为偶数，所以再进展一次二项移动平均，即得出中心化移动平均值.可修编.\n.-三、计算移动平均的比值〔移动平均比值=销售额/中心化移动平均值〕四、计算得出季节指数〔季节指数=各年同季度的平均数/各年所有季度的总平均数〕五、计算季节别离后的序列〔季节别离后的序列=销售额/季节指数〕六、对数据进展回归分析并且求出回归方程.可修编.\n.-回归方程为Y=1970.1908+168.5382t线性拟合图如下所示：由此图可以看出预测值与实际值线性拟合度较高七、得出回归预测值以及最终预测值〔最终预测值=回归预测值/季节指数〕八、计算出出季节成分别离后的销售额并画出其趋势图.可修编.\n.-九、2021年各季度销售额预测值图表及其折线图十、实验结论由上一步表格中的数据可以看出该百货公司销售额总的来说是上涨的，第三季度销售额最高，第一以及第二季度销售额相对来说比拟低；从上一步的折线图来看，预测值在某些年份的某些季度有较大的误差，但是总的来说预测效果还是不错的。教育之通病是教用脑的人不用手，不教用手的人用脑，所以一无所能。教育革命的对策是手脑联盟，结果是手与脑的力量都可以大到不可思议。.可修编.