- 2022-08-13 发布 |
- 37.5 KB |
- 25页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
统计学734494
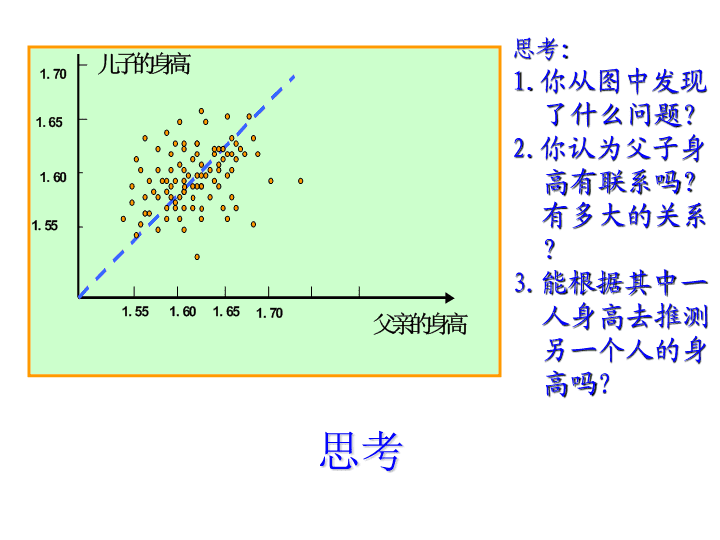
思考:1.你从图中发现了什么问题?2.你认为父子身高有联系吗?有多大的关系?3.能根据其中一人身高去推测另一个人的身高吗?思考\n第七章相关分析\n1.了解相关关系的涵义与种类,掌握相关分析的基本方法,相关系数含义和计算,相关关系的判定原则;2.了解回归分析的含义与类型,理解相关与回归分析的联系与特点;3.掌握一元线性回归模型建立的条件、参数求解方法,回归模型的评价依据,4.初步认识回归分析在预测中的应用。教学内容与要求:\n现象之间存在的确定性的数量关系现象之间存在的不确定性的数量关系如:同卵双胞胎间的身高、收入和受教育程度、身高和体重、婴儿月龄与身高函数关系相关关系如:正方形面积与边长的关系:联系:函数关系如果存在测量误差,则表现为相关关系,相关关系通常使用函数关系形式来表现。7.1相关分析的意义和任务一、相关关系的概念2aS=\n因素多少表现形态相关性质相关程度单相关曲线相关负相关不相关复相关直线相关正相关完全相关不完全相关二、相关关系的种类\n不相关负线性相关正线性相关非线性相关完全负线性相关完全正线性相关散点图\n1确定现象之间有无关系及表现形式2确定相关关系的密切程度3选择合适的数学模型4测定变量估计值的可靠程度5对相关系数作显著性检验三、相关分析的主要内容\n温度(度)28282929293031313132销售量(箱)808584889598105102110116一、相关图与相关表7.2简单线性相关分析\n1单变量分组图表:只根据一个变量分组分组相关图和相关表使用年限机床数(台)平均维修费用()224703152042690527006378781840911080合计12__\n2双变量分组图表:自变量和因变量都进行分组年维修费用(元)机床使用年限(年)合计23456891000—110011900—100011800—900112700—800123600—700112500—600112400—50011合计212231112\n反映两个变量线性相关密切程度的指标。二、相关系数的测定与应用1相关系数2计算方法:积差法P334例题简捷公式\n温度x(度)28282929293031313132销售量y(箱)808584889598105102110116\n3相关系数r特点:r没有单位,其大小不受下列因素的影响:①互换两个变量的位置②某一变量的所有值都增加同一数值③某一变量的所有值都乘以同一正数4相关系数r的密切程度意义:①r∈[-1,+1]②当r<0时,负相关当r>0时,正相关当r=0时,无相关0.8≤|r|<1:高度相关0.5≤|r|<0.8:显著相关0.3≤|r|<0.5:低度相关0≤|r|<0.3:微相关\n确定变量间的定量关系式预测和控制对关系式作各种统计检验判断各变量的影响显著性一、回归分析的概念对具有相关关系的变量之间数量变化的一般关系进行测定,确定一个数学表达式以进行估计或预测的统计方法。7.3回归分析1回归分析2回归分析的内容\n相关分析与回归分析的比较联系相关分析依靠回归分析表明现象间数量关系的具体形式;回归分析要以相关分析为基础。区别◆分析内容不同相关分析只研究变量间相关的方向和程度。不必确定因变量和自变量;所有变量都可以是随机变量;改变变量的位置不影响相关分析的结果回归分析研究变量间相关的具体形式必须先确定因变量与自变量;一般只有因变量是随机变量,自变量是非随机变量;交换变量的位置,回归方程不同,只能根据自变量推算因变量。\n二、回归的种类线性回归、非线性回归一元回归、多元回归三、直线回归(简单直线回归)1在两个变量之间进行回归分析时,必需根据研究目的,确定哪个是自变量,哪个是因变量。2在两个现象互为根据的情况下,可以有两个回归方程。3回归方程的作用在于给出自变量的数值来估计因变量的可能值。1特点:\n2直线回归方程的确定:最小平方法基本形式:yc=a+bx其中a,b为未知参数,根据最小平方法的要求,从∑(y-yc)2最小出发,得到解出22)x(n1xyxn1xybxbya--=-=ååååå\n88036.4合计1608.081357.271326.161155.051103.84803.13862.02621.21生产费用万元y产品产量千吨x序号442.42748804544.6207.5430.1401154.51128064.0084.4561144.1997251.844130805.237.210.6561115.8157525.0093.5089100.3341814.11127.6991.32489.6179.032177.111724.0022.944166.7974.41.44(y-yc)2ycxyx2例题(338,342)\n7.4估计标准误差一、估计标准误差的概念(回归)估计标准误差因变量的各个观察值与估计值(拟合值)的平均离差,是判断回归方程代表性的大小的统计分析指标。二、简单直线回归估计标准误差的测定1根据因变量实际值和估计值的离差计算2n)ycy(s2yx--=å样本公式\n2根据a、b两个参数计算2nxybyays2yx---=ååå简捷公式[]ååååååååååååååååååååå--=++--=++++--=+++--=+-=-xybyayxybyaxyb2ya2y)xbxa(b)xbna(axyb2ya2yxbxab2naxyb2ya2y)bxa(y)ycy(2222222222\n总离差平方和剩余离差平方和回归离差平方和说明因变量的总离差平方和可以用回归模型来解释的比例。三、相关系数和估计标准误差的关系21ryyx-=ss2221ryyx+=ss1关系\n\n2根据a、b两个参数计算rr值越大,syx越小。即相关程度越密切,估计标准误差越小r值越小,syx越大。即相关程度越不密切,估计标准误差越大。实际中,一般不常用这种方法计算r,因为,(1)需要先求出回归直线方程,计算出估计标准误差,才能求得r。不符合一般程序。(2)以这种方法计算的r难以判断是正相关还是负相关。\n例:某蔬菜公司进行贮存试验,观察贮存时间对维生素的影响。将500克放在恒温的容器内,每隔一小时测量维生素C的含量,得出如下数据:(1)计算贮存时间与维生素含量的相关系数(2)计算维生素含量的理论值时间(x)012345维生素含量201817151413理论含量值19.6718.2616.8715.4614.0712.67估计误差0.33-0.260.13-0.46-0.070.33\n解:(2)建立贮存时间与维生素含量的回归方程(1)(3)回归估计标准误差:9852.02=r查看更多