心理统计学

心理统计学

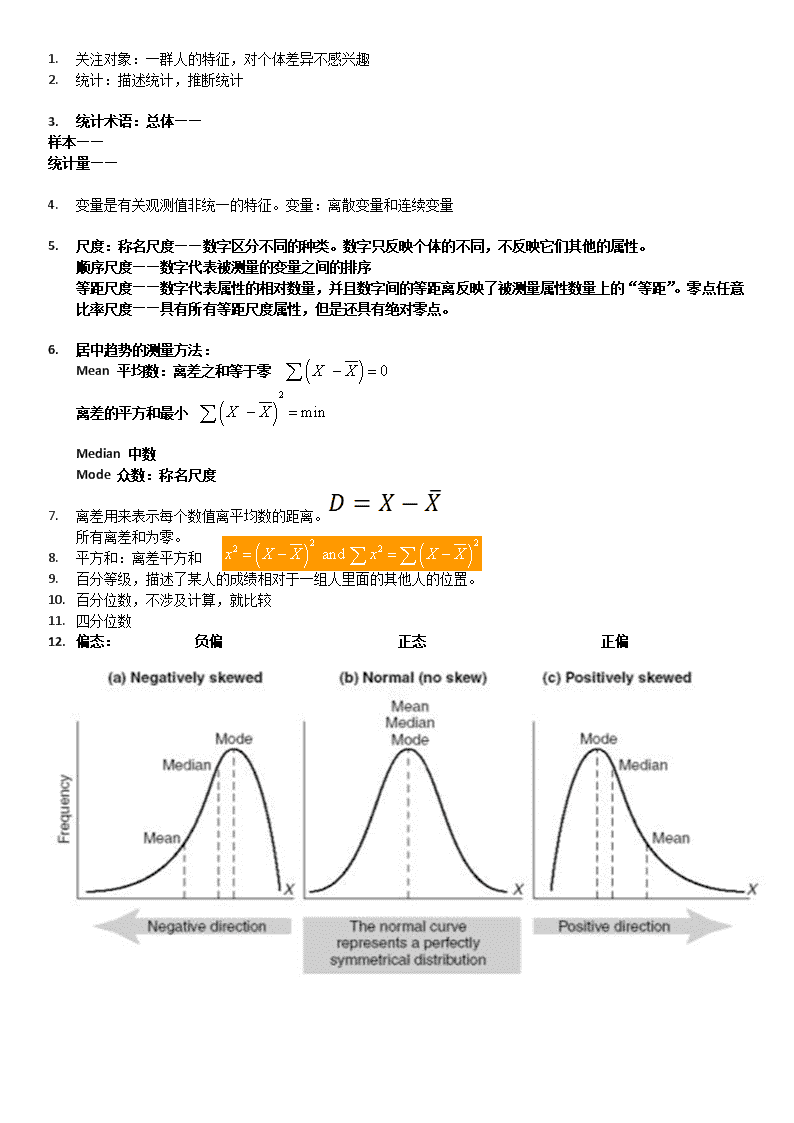
1.关注对象：一群人的特征，对个体差异不感兴趣2.统计：描述统计，推断统计3.统计术语：总体——样本——统计量——1.2.3.4.变量是有关观测值非统一的特征。变量：离散变量和连续变量5.尺度：称名尺度——数字区分不同的种类。数字只反映个体的不同，不反映它们其他的属性。顺序尺度——数字代表被测量的变量之间的排序等距尺度——数字代表属性的相对数量，并且数字间的等距离反映了被测量属性数量上的“等距”。零点任意比率尺度——具有所有等距尺度属性，但是还具有绝对零点。6.居中趋势的测量方法：Mean平均数：离差之和等于零离差的平方和最小Median中数Mode众数：称名尺度7.离差用来表示每个数值离平均数的距离。所有离差和为零。8.平方和：离差平方和9.百分等级，描述了某人的成绩相对于一组人里面的其他人的位置。10.百分位数，不涉及计算，就比较11.四分位数12.偏态：负偏正态正偏\n1.峰度，峭度2.散点图：总的来说，点越是接近一条直线，相关越高3.皮尔逊相关系数代表两个连续变量之间的线性关系系数ρ(r)代表两个变量之间关系的方向和大小。Sxy是协方差，即x和y一起变化的程度协方差取决于两个变量所处的尺度。所以，把它除以标准差使得它们“标准化”。如果没有关系，协方差是0.004.相关关系：完全正相关r=+1.00；完全负相关r=-1.00r=0,r绝对值趋近0时，相关性小；r绝对值趋近1时，相关性大5.相关并不意味着因果。6.标准分计算：7.抽样分布：一个抽样分布是样本统计值的次数分布，而不是原始数据的次数分布。.样本统计值的不同是由于抽样误差，因为我们没有包含总体中所有可能的数值一个统计量抽样分布的中间位置都是该统计量对应的的总体的值。样本容量越大，分布越窄，分布的标准差越小。8.平均数的抽样分布是从一个总体抽出的可能的样本平均数的分布。（计算）9.平均数的标准误：样本增大，平均数的标准误变小。随着平均数的标准误变小，抽样误差变小10.推断统计：假设检验：零假设对应的是没有差异的那个抽样分布。Ho不显著效应；研究假设/备择假设这个假设对应的是有差异的抽样分布。H1显著效应假设的陈述要根据总体，而不是样本。11.Z检验和t检验12.两种错误和犯错误的大小13.在单侧检验中，零假设是没有差异，或者差异的方向错误14.怎样增加功效：增大样本容量；增大Alpha；增大效应度15.区间估计置信区间：我们设置在围绕观察到的统计量的一个区域，来检验假设的参数看零假设中的总体参数是否落在置信区间里，如果是，那我们说差异是因为偶然；如果零假设的总体参数落在区间内，那么我们说差异是因为我们的实验。？？16.自由度是一个值，它显示以统计推断目的的一个样本能够提供的独立信息的个数。随着自由度的增大，t关键值越来越接近z关键值\n1.单样本t检验2.独立样本t检验独立个案代表从总体抽取的随机的样本。3.t配对样本t4.:零假设为真时，平均数之差的抽样分布的平均数5.平均数之差的标准误：平均数之差的抽样分布的标准差6.如果两个总体的分布都是正态的，那么这个抽样分布是正态的。7.标准误的估计：方差齐性假定8.前测-后侧实验设计假设；关键值；自由度；9.t检验中的效应度10.功效：当零假设为假时，据绝零假设的概率Power=1–β增大样本容量；增加第一类错误；增加效应度11.回归：平方和最小准则：拟合最好的线使得误差的平方最小可视化误差回归系数：b0：当X=0时预测的Y的平均值；b1：保持其它不变，X增加一个单位，Y平均的变化量12.解构方差/离差/变异总方差=回归方差+误差方差13.R2是有偏统计量，因为它过高估计了总体中的R214.统计推断15.多元回归最小平方估计：选择能使误差的平方和最小的模型来估计参数回归的斜率系数是在保持其它不变的情况下，X改变一个单位，Y平均的变化\n当回归模型中有其它预测值/自变量时，偏回归系数是某个预测值/自变量的权重。R2在Y中能被线性模型解释的方差的比率1-R2是Y中不能被预测的/解释的方差的比率方差分析高度多重共线性会导致回归系数的估计不稳定。1.两因素组间方差分析2.单因素协方差分析在于评估当控制协变量的差异的时候，在总体中因变量在因素的不同水平间是否有差异。3.卡方检验4.两因素列联表