基本统计学

基本统计学

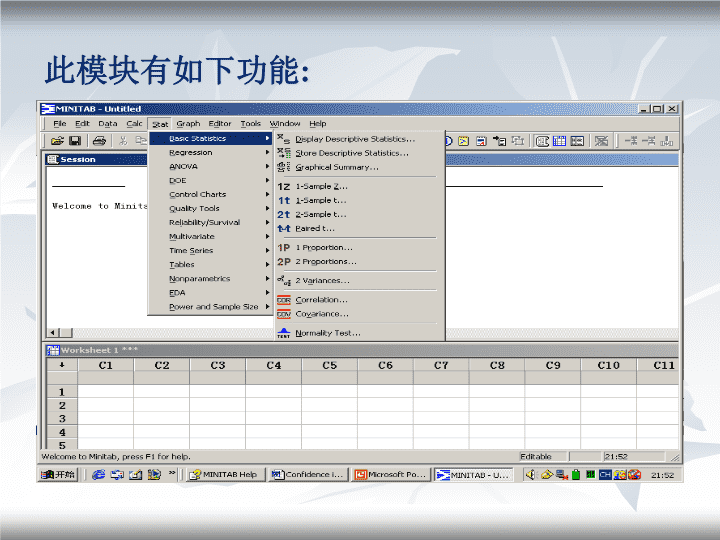
MINITAB培训(工程师级)------BasicStatistics模块\n此模块有如下功能:\n模块功能UseMinitab'sbasicstatisticscapabilitiesforcalculatingbasicstatisticsandforsimpleestimationandhypothesistestingwithoneortwosamples.Thebasicstatisticscapabilitiesincludeproceduresfor:CalculatingorstoringdescriptivestatisticsHypothesistestsandconfidenceintervalsofthemeanordifferenceinmeansHypothesistestsandconfidenceintervalsforaproportionorthedifferenceinproportionsHypothesistestforequalityofvarianceMeasuringassociationTestingfornormalityofadistribution\n打开一个软件自带的例子学习\n打开Quality文件\n数据如下\n选择显示描述性统计\n填完自变量和因变量后,点击Graphs按钮\n\n点击OK后,显示出箱线图和统计数据\n解释每个箱线图最低点表示当天最小值,最高点表示最大值,箱子高,低点分别表示3/4,1/4数字大小,箱中间一横表示当天几个数据的中位数在Session窗口中具体显示MEAN平均值,StDev标准差,Median中位数等信息.\n选择存贮描述性统计\n填完自变量和因变量后,点击OK\n多了些数据,自动将统计的数据如平均值和每日数据量N=10存放在C3-C5列\n用图形概要方式\n如图,点击OK\nTheleftfourgraphs:histogramofdatawithanoverlaidnormalcurve(带常态曲线的柱状图),boxplot箱线图),95%confidenceintervalsformean,and95%confidenceintervalsforthemedian.(平均值和中位数95%的置信区间范围图)\n右边第一块数据是正态性检验.显示P-Value=0.661,大于0.05,所以数据符合正态分布.第二块数据是平均值,偏态等第三块数据是最小最大等第四块数据是平均值,方差的95%置信区间等\n区间估计与假设检验例假设一个物体的重量未知,为了估计其重量,用一个天平称5次,得到重量5.525.485.645.515.45,假设结果符合标准差0.1的正态分布,求均值是否是5.5和重量置信水平为95%的置信区间\n输入数据后,按图所示\n按图所示将例子中数据填入后点击OK\n得到分析结果见Session窗口\n分析One-SampleZ:C1Testofmu=5.5vsnot=5.5Theassumedstandarddeviation=0.1VariableNMeanStDevSEMean95%CIZPC155.520000.072460.04472(5.43235,5.60765)0.450.655由于假设均值为5.5,而置信区间(5.43235,5.60765)包含了5.5,故假设成立,可以认为重量为5.5\n当前一例子中方差未知时(这也是通常的情况),求重量是否可认为是5.5\n如图填上数据,点击OK\n结果在Session窗口中显示\n解释One-SampleT:C1Testofmu=5.5vsnot=5.5VariableNMeanStDevSEMean95%CITPC155.520000.072460.03240(5.43003,5.60997)0.620.570同样的,5.5在(5.43003,5.60997)范围中,可认为假设均值5.5成立.\n一个新例子公司购买了同型号的两台机床(可认为其加工的零件尺寸服从同方差的正态分布),抽检两台机床加工的轴,分析两台机床加工的轴有无明显差异机床甲:20.5/19.8/19.7/20.4/21.1/20/19/19.9机床乙:20.7/19.8/19.5/20.8/20.4/19.6/20.2\n输入数据于两列中\n\n\n\nTwo-sampleTforC1vsC2NMeanStDevSEMeanC1820.0500.6260.22C2720.1430.5220.20Difference=mu(C1)-mu(C2)Estimatefordifference:-0.09285795%CIfordifference:(-0.738860,0.553146)T-Testofdifference=0(vsnot=):T-Value=-0.31P-Value=0.760DF=12由于假设两均值相等,差为0,在(-0.738860,0.553146)中,故可认为二者均值无明显差异\n假设方差未知,判断两个总体的方差是否相等,即尺寸离散度是否相同\n\n