2020届二轮复习解三角形学案(全国通用)(1)
年 级: 辅导科目:数学 课时数:
课 题 解三角形
教学目的
教学内容
第一节 正弦定理和余弦定理
(一)高考目标
考纲解读
掌握正弦定理、余弦定理,并能解决一些简单的三角形度量问题.
考向预测
1.利用正弦定理、余弦定理进行边角转化,进而进行恒等变形解决问题.
2.与三角形有关的问题在考查正弦定理、余弦定理和面积公式的同时,考查三角恒等变形,这是高考的热点.
3.三种题型均有可能出现,属中低档题目.
(二)课前自主预习
知识梳理
1. 正弦定理和余弦定理
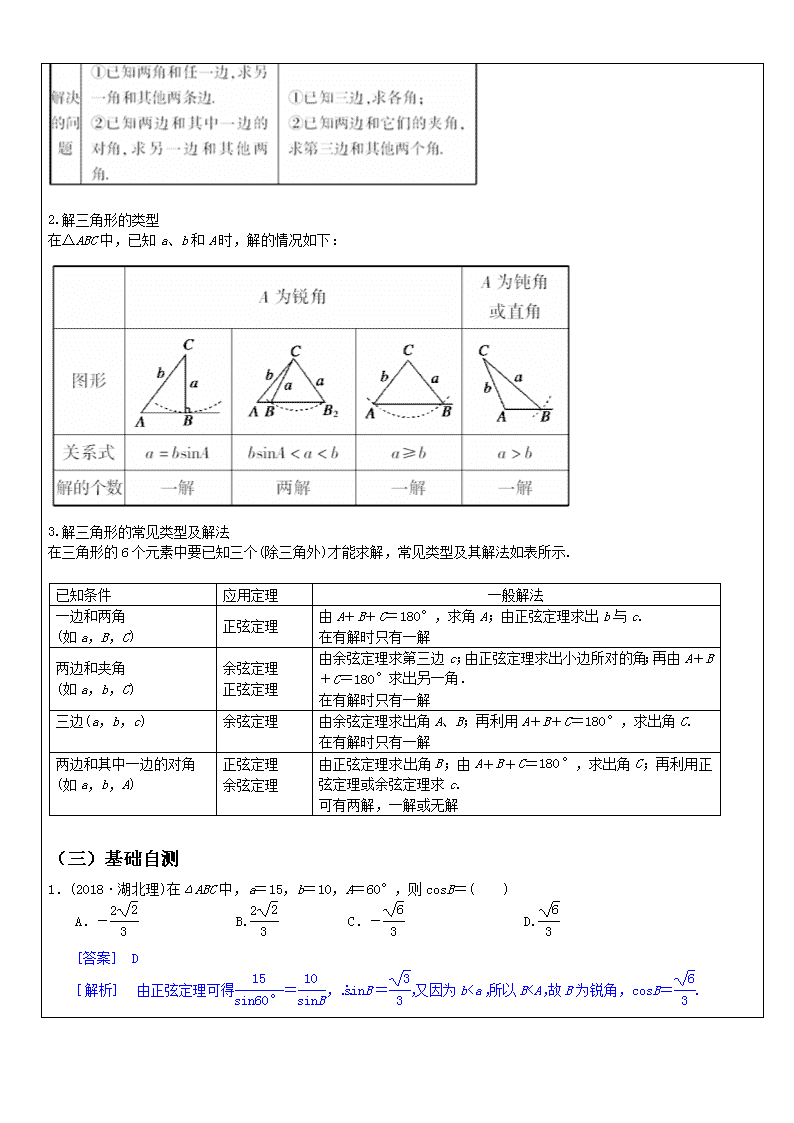
2.解三角形的类型
在△ABC 中,已知 a、b 和 A 时,解的情况如下:
3.解三角形的常见类型及解法
在三角形的 6 个元素中要已知三个(除三角外)才能求解,常见类型及其解法如表所示.
已知条件 应用定理 一般解法
一边和两角
(如 a,B,C) 正弦定理 由 A+B+C=180°,求角 A;由正弦定理求出 b 与 c.
在有解时只有一解
两边和夹角
(如 a,b,C)
余弦定理
正弦定理
由余弦定理求第三边 c;由正弦定理求出小边所对的角;再由 A
+B+C=180°求出另一角.
在有解时只有一解
三边(a,b,c) 余弦定理 由余弦定理求出角 A、B;再利用 A+B+C=180°,求出角 C.
在有解时只有一解
两边和其中一边的对角
(如 a,b,A)
正弦定理
余弦定理
由正弦定理求出角 B;由 A+B+C=180°,求出角 C;再利用正
弦定理或余弦定理求 c.
可有两解,一解或无解
(三)基础自测
1.(2018·湖北理)在ΔABC 中,a=15,b=10,A=60°,则 cosB=( )
A.-2 2
3
B.2 2
3
C.- 6
3
D. 6
3
[答案] D
[解析] 由正弦定理可得 15
sin60°
= 10
sinB
,∴sinB= 3
3
,又因为 b
0,
∴a2>b2,a>b.
5.△ABC 的内角 A,B,C 的对边分别为 a,b,c.若 c= 2,b= 6,B=120°,则 a=________
[答案] 2
[解析] 由余弦定理得 b2=a2+c2-2accos120°,
即 6=a2+2-2a· 2·
-1
2 ⇒a= 2或 a=-2 2(舍去).
6.在△ABC 中,若 sinC=2cosAsinB,则此三角形是________三角形.
[答案] 等腰
[解析] 由 sinC=2cosAsinB,得 sin(A+B)=2cosAsinB,
即 sinAcosB+cosAsinB=2cosAsinB,
即 sinAcosB-cosAsinB=0,
所以 sin(A-B)=0.
又因为-πc>b,∴角 A 为最大角
由余弦定理有 cosA=b2+c2-a2
2bc
=-1
2
,
∴A=120°,∴sinA= 3
2
,
再根据正弦定理,有 a
sinA
= c
sinC
,
∴sinC=c
a
sinA=5
7
× 3
2
=5 3
14
.
2.命题方向:与面积有关的问题
[例 2] 在△ABC 中,A=60°,b=1,其面积为,则△ABC 外接圆的直径是________.
[分析] 三角形外接圆直径是和正弦定理联系在一起的,已经知道了 A=60°,只要再能求出边 a,问题就解决了,
结合已知条件求边 a 是解决问题的关键.
[解析] 由题意知,S△ABC=1
2
bcsinA,所以 c=4.
由余弦定理知:a= b2+c2-2bccosA= 13,
再由正弦定理 2R= a
sinA
=
13
3
2
=2 39
3
.
即△ABC 外接圆的直径是2 39
3
.
[答案] 2 39
3
跟踪练习 2 :
(2018·江苏)满足条件 AB=2,AC= 2BC 的△ABC 的面积的最大值为________.
[答案] 2 2
[解析] 设 BC=x,则 AC= 2x,根据面积公式得
S△ABC=1
2
AB·BC·sinB
=1
2
×2x 1-cos2B①
根据余弦定理得
cosB=AB2+BC2-AC2
2AB·BC
=4+x2- 2x 2
4x
=4-x2
4x
,
代入①式可得
S△ABC=x 1-
4-x2
4x 2= 128- x2-12 2
16
,
由三角形三边关系有
2x+x>2,
x+2> 2x,
解得 2 2-20,
则 a=ksinA,b=ksinB,c=ksinC 代入已知条件得
ksinAcosA+ksinBcosB=ksinCcos C,
即 sinAcosA+sinBcosB=sinCcosC.
根据二倍角公式得 sin2A+sin2B=sin2C,
sin[(A+B)+(A-B)]+sin[(A+B)-(A-B)]=2sinCcosC,
∴2sin(A+B)cos(A-B)=2sinCcosC.
∵A+B+C=π⇒A+B=π-C,
∴sin(A+B)=sinC≠0,
∴cos(A-B)=cosC,∴cos(A-B)+cos(A+B)=0,
∴2cosAcosB=0⇒cosA=0 或 cosB=0,
即 A=90°或 B=90°,∴△ABC 是直角三角形.
方法二:由余弦定理知
cosA=b2+c2-a2
2bc
,cosB=a2+c2-b2
2ac
,cosC=a2+b2-c2
2ab
,
代入已知条件得
a·b2+c2-a2
2bc
+b·a2+c2-b2
2ac
+c·c2-a2-b2
2ab
=0,
化简得
a2(b2+c2-a2)+b2(a2+c2-b2)+c2(c2-a2-b2)=0,
展开整理得(a2-b2)2=c4,∴a2-b2=±c2,
即 a2=b2+c2 或 b2=a2+c2.
根据勾股定理知△ABC 是直角三角形.
跟踪练习 3:△ABC 中,a2tanB=b2tanA,判断三角形的形状是( )
A.等腰三角形 B.直角三角形
C.等腰三角形或直角三角形 D.等腰直角三角形
[答案] C
[解析] 由正弦定理得 sin2AtanB=sin2BtanA,
sinAcosA=sinBcosB,即 sin2A=sin2B.
又因为 A,B∈(0,π),所以 A=B 或 A+B=90°.
4.命题方向:正、余弦定理的综合应用
[例 4] △ABC 中,角 A,B,C 的对边分别为 a,b,c 且 b2+c2-a2+bc=0.
(1)求角 A 的大小;
(2)若 a= 3,求 bc 的最大值;
(3)求asin30°-C
b-c
的值.
[分析] (1)由 b2+c2-a2+bc=0 的结构形式,可联想余弦定理,求出 cosA,进而求出 A 的值.
(2)由 a= 3及 b2+c2-a2+bc=0,可求出关于 b,c 的关系式,利用不等式即可求出 bc 的最大值.
(3)由正弦定理可实现将边化角的功能,从而达到化简求值的目的.
[解析] (1)∵cosA=b2+c2-a2
2bc
=-bc
2bc
=-1
2
,
∴A=120°.
(2)由 a= 3,得 b2+c2=3-bc.
又∵b2+c2≥2bc(当且仅当 c=b 时取等号),
∴3-bc≥2bc(当且仅当 c=b 时取等号),
即当且仅当 c=b=1 时,bc 取得最大值为 1.
(3)由正弦定理,得 a
sinA
= b
sinB
= c
sinC
=2R,
∴asin (30°-C)
b-c
=2RsinAsin (30°-C)
2RsinB-2RsinC
=sinAsin (30°-C)
sinB-sinC
=
3
2
1
2
cosC- 3
2
sinC
sin (60°-C) -sinC
=
3
4
cosC-3
4
sinC
3
2
cosC-3
2
sinC
=1
2
.
跟踪练习 4:在△ABC 中,A、B、C 所对的边长分别为 a,b,c,设 a,b,c 满足条件 b2+c2-bc=a2 和c
b
=1
2
+ 3,
求 A 和 tanB 的值.
[解析] 由余弦定理 cosA=b2+c2-a2
2bc
= bc
2bc
=1
2
,
因此 A=60°.
在△ABC 中,C=180°-A-B=120°-B.
由已知条件,应用正弦定理
1
2
+ 3=c
b
=sinC
sinB
=sin 120°-B
sinB
=sin120°cosB-cos120°sinB
sinB
= 3
2
cotB+1
2
,
解得 cotB=2,从而 tanB=1
2
.
(五)思想方法点拨
1.在利用正弦定理解决已知三角形的两边和其中一边的对角解三角形问题时,可能出现一解、两解或无解情况,应
结合图形并根据“三角形中大边对大角”来判断解的情况,作出正确取舍.
2.在判断三角形的形状时,一般将已知条件中的边角关系利用正弦定理或余弦定理转化为角角的关系或边边的关系,
再用三角变换或代数式的恒等变形(如因式分解、配方等)求解.注意等式两边的公因式不要约掉,要移项提取公因式,
否则会有漏掉一种形状的可能.
3.一般地,由 sinα>sinβ⇒/ α>β,但在△ABC 中,sinA>sinB⇔A>B.
4.判断三角形形状的方法
根据所给条件确定三角形的形状,主要有两条途径:(1)化边为角;(2)化角为边.具体有如下四种方法:①通过正弦
定理实施边、角转换;②通过余弦定理实施边、角转换;③通过三角变换找出角之间的关系;④通过三角函数值符号
的判断及正、余弦函数有界性的讨论;⑤b2+c2-a2>0⇔A 为锐角,b2+c2-a2=0⇔A 为直角,b2+c2-a2<0⇔A 为
钝角.
(六)课后强化作业
一、选择题
1.在△ABC 中,AB= 3,A=45°,C=75°,则 BC 等于( )
A.3- 3 B. 2 C.2 D.3+ 3
[答案] A
[解析] 由 AB
sinC
= BC
sinA
得 BC=3- 3.
2.(2018·安徽)在三角形 ABC 中,AB=5,AC=3,BC=7,则∠BAC 的大小为( )
A.2π
3
B.5π
6
C.3π
4
D.π
3
[答案] A
[解析] cos∠BAC=AB2+AC2-BC2
2AB·AC
=-1
2
.
∵0<∠BAC<π,∴∠BAC=2π
3
.
3.在△ABC 中,cos2A
2
=b+c
2c
,则△ABC 的形状为( )
A.直角三角形 B.等腰三角形或直角三角形
C.正三角形 D.等腰直角三角形
[答案] A
[解析] ∵cos2A
2
=b+c
2c
,∴1+cosA
2
=b+c
2c
,
即 cosA=b
c
,又由余弦定理知,
cosA=b2+c2-a2
2bc
,∴b2+c2-a2
2bc
=b
c
,
∴a2+b2=c2,∴△ABC 为直角三角形.
4.(2018·天津理)在△ABC 中,内角 A,B,C 的对边分别是 a,b,c,若 a2-b2= 3bc,sinC=2 3sinB,
则 A=( )
A.30° B.60° C.120° D.150°
[答案] A
[解析] 由余弦定理得:cosA=b2+c2-a2
2bc
,
由题知 b2-a2=- 3bc,c2=2 3bc,则 cosA= 3
2
,
又 A∈(0°,180°),∴A=30°,故选 A.
5.已知△ABC 的三个内角为 A、B、C,所对的三边分别为 a、b、c,若△ABC 的面积为 S=a2-(b-c)2,则 tan A
2
等于( )
A.1
2
B.1
4
C.1
8
D.1
[答案] B
[解析] 由于 S=1
2
bcsinA,又 S=a2-b2-c2+2bc,由余弦定理知 a2-b2-c2=-2bccosA,
∴1
2
bcsinA=-2bccosA+2bc⇒sinA=4(1-cosA)
⇒2sinA
2
cosA
2
=4×2sin2A
2
⇒tanA
2
=1
4
.
6.锐角三角形 ABC 中,a、b、c 分别是三内角 A、B、C 的对边,设 B=2A,则b
a
的取值范围是( )
A.(-2,2) B.(0,2) C.( 2,2) D.( 2, 3)
[答案] D
[解析] ∵b
a
=sinB
sinA
=sin2A
sinA
=2cosA,又△ABC 是锐角三角形,∴
B=2A<90°
A+2A>90°
∴30°b 知 c=6,b=4.
14.(2009·浙江理)在△ABC 中,角 A,B,C 所对的边分别为 a,b,c,且满足 cosA
2
=2 5
5
,AB→·AC→=3.
(1)求△ABC 的面积;
(2)若 b+c=6,求 a 的值.
[解析] 本题主要考查正弦、余弦定理、三角公式变换、三角形面积公式及向量运算等基础知识,同时考查运算
求解能力.
(1)因为 cosA
2
=2 5
5
,
所以 cosA=2cos2A
2
-1=3
5
,sinA=4
5
.
又由AB→·AC→=3,得 bccosA=3,所以 bc=5.
因此 S△ABC=1
2
bcsinA=2.
(2)由(1)知,bc=5,又 b+c=6,
所以 b=5,c=1 或 b=1,c=5
由余弦定理,得 a2=b2+c2-2bccosA=20,
所以 a=2 5.
15.已知△ABC 中,a、b、c 分别是角 A、B、C 的对边,且 3sin2B+3sin2C-2sinBsinC=3sin2A,a= 3,求AB→·AC→
的最大值.
[分析] 所给条件式为角的关系,又均为“二次”式,故化角为边后可利用余弦定理寻求联系求解.
[解析] ∵3sin2B+3sin2C-2sinBsinC=3sin2A,由正弦定理得 3b2+3c2-2bc=3a2,即 3b2+3c2-3a2=2bc,再
由余弦定理得 cosA=b2+c2-a2
2bc
=1
3
.
∵a= 3,∴3b2+3c2-2bc=9≥6bc-2bc=4bc,
∴bc≤9
4
,当且仅当 b=c 时等号成立.
∴AB→·AC→=c·b·cosA=bc
3
≤3
4
,
故AB→·AC→的最大值为3
4
.
第二节 正弦、余弦定理的应用举例
(一)高考目标
考纲解读
能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的实际问题.
考向预测
1.对解决实际问题的能力及测量问题的考查是高考的重点.
2.在选择、填空、解答中都可能考查,属中档题.
(二)课前自主预习
知识梳理
1.仰角和俯角
与目标线在同一铅垂平面内的水平视线和目标视线的夹角,目标视线在水平视线 叫仰角,目标视线在水
平视线 叫俯角(如图①).
2.方位角
指从 方向顺时针转到目标方向线的水平角,如 B 点的方位角为α(如图②).
3.方向角:相对于某一正方向的水平角(如图③)
①北偏东α°:指北方向顺时针旋转α°到达目标方向.
②东北方向:指北偏东 45°或东偏北 45°.
③其他方向角类似.
4.坡度:坡面与水平面所成的二面角的度数(如图④,角θ为坡角).
坡比:坡面的铅直高度与水平长度之比(如图④,i 为坡比).
(三)基础自测
1.若点 A 在点 B 的北偏西 30°,则 B 点在 A 点的( )
A.西偏北 30° B.西偏北 60° C.南偏东 30° D.东偏南 30°
[答案] C
[解析] 由图可知 B 在 A 的南偏东 30°.
2.一人向东走了 xkm 后转向南偏西 60°走了 3km,结果他离出发点恰好 3km,则 x 的值为( )
A. 3 B.2 3 C.2 3或 3 D.3
[答案] C
[解析] 如图所示,在△ABC 中,AB=x,BC=3,AC= 3,∠ABC=30°,由余弦定理得,
( 3)2=32+x2-2×3×x×cos30°,
即 x2-3 3x+6=0,解得 x1= 3,x2=2 3.经检验均合题意.
3.(教材改编题)在某次测量中,在A 处测得同一半平面方向的B 点的仰角是60°,C点的俯角为 70°,则∠BAC=( )
A.10° B.50° C.120° D.130°
[答案] D
[解析] 如图,由已知∠BAD=60°,∠CAD=70°,
∴∠BAC=60°+70°=130°.
4.(教材改编题)有一长为 1 的斜坡,它的倾斜角为 20°,现高不变,将倾斜角改为 10°,则斜坡长为( )
A.1 B.2sin10° C.2cos10° D.cos20°
[答案] C
[解析] 如图,∵∠ABC=20°,AB=1,∠ADC=10°,
∴∠ABD=160°.
在△ABD 中,由正弦定理 AD
sin160°
= AB
sin10°
,
∴AD=AB·sin160°
sin10°
=sin20°
sin10°
=2cos10°.
5.(2018·南京模拟)如图,测量河对岸的塔高 AB 时,可以选与塔底 B 在同一水平面内的两个测点 C 与 D.测得∠BCD
=15°,∠BDC=30°,CD=30m,并在点 C 测得塔顶 A 的仰角为 60°,则塔高 AB=________m.
[答案] 15 6
[解析] 由已知可得∠DBC=135°,
在△DBC 中,由正弦定理可得 BC
sin30°
= CD
sin135°
,
BC=CDsin30°
sin135°
=30×sin30°
sin135°
=15 2,
∴AB=BCtan60°=15 2× 3=15 6.
6.在△ABC 中,已知 AC=3,sinA+cosA= 2.
(1)求 sinA 的值;
(2)若△ABC 的面积 S=3,求 BC 的值.
[解析] (1)由 sinA+cosA= 2sin
A+π
4 = 2得
sin
A+π
4 =1,由此及 00,∴x= 6-1.
7.如图,在坡度一定的山坡 A 处测得山顶上一建筑物 CD 的顶端 C 对于山坡的斜度为 15°,向山顶前进 100 米
到达 B 后,又测得 C 对于山坡的斜度为 45°,若 CD=50 米,山坡对于地平面的坡角为θ,则 cosθ=( )
A. 3
2
B.2- 3 C. 3-1 D. 2
2
[答案] C
[解析] 在△ABC 中,BC=ABsin∠BAC
sin∠ACB
= 100sin15°
sin 45°-15°
=50( 6- 2),
在△BCD 中,sin∠BDC=BCsin∠CBD
CD
=50 6- 2 sin45°
50
= 3-1,
由图知 cosθ=sin∠ADE=sin∠BDC= 3-1.
8.空中有一气球,在它的正西方 A 点测得它的仰角为 45°,同时在它南偏东 60°的 B 点,测得它的仰角为 30°,
若 A,B 两点间的距离为 266 米,这两个观测点均离地 1 米,那么测量时气球到地面的距离是( )
A.266 7
7
米 B.
266 7
7
+1
米 C.266 米 D.266 7米
[答案] B
[解析] 如图,D 为气球 C 在过 AB 且与地面平行的平面上的正投影,设 CD=x 米,依题意知:∠CAD=45°,∠
CBD=30°,则 AD=x 米,BD= 3x 米.在△ABD 中,由余弦定理得 AB2=AD2+BD2-2AD·BD·cos∠ADB,即 2662=x2
+( 3x)2-2x·( 3x)·cos150°=7x2,解得 x=266 7
7
,故测量时气球到地面的距离是
266 7
7
+1
米,故选 B.
二、填空题
9.海上有 A、B 两个小岛相距 10 海里,从 A 岛望 C 岛和 B 岛成 60°的视角,从 B 岛望 C 岛和 A 岛成 75°的视角,
则 B、C 的距离是________.
[答案] 5 6海里
[解析] 在△ABC 中由正弦定理得 10
sin45°
= BC
sin60°
,
∴BC=5 6.
10.我舰在岛 A 南 50°西 12 海里的 B 处,发现敌舰正从岛沿北 10°西的方向以每小时 10 海里的速度航行,若
我舰要用 2 小时追上敌舰,则速度为________.
[答案] 14 海里/小时
[解析] 设我舰在 C 处追上敌舰,速度为 V,则在△ABC 中,AC=20,AB=12,∠BAC=120°.
∴BC2=784,∴V=14 海里/小时.
11.2009 年 8 月 9 日,莫拉克台风即将登陆福建省霞浦县,如图,位于港口 O 正东方向 20 海里的 B 处的渔船回
港避风时出现故障.位于港口南偏西 30°方向,距港口 10 海里的 C 处的拖轮接到海事部门营救信息后以 30 海里/小
时的速度沿直线 CB 去营救渔船,则拖轮到 B 处需要________小时.
[分析] 求解本题的关键是把实际应用问题转化为数学问题,然后再利用余弦定理解决.
[答案] 7
3
[解析] 由题易知,∠BOC=120°,因为 BC2=OC2+OB2-2·OC·OB·cos120°=700,所以 BC=10 7,所以拖
轮到达 B 处需要的时间 t=10 7
30
= 7
3
(小时).
三、解答题
12.如图某货轮在 A 处看灯塔 B 在货轮的北偏东 75°,距离为 12 6n mile,在 A 处看灯塔 C 在货轮的北偏西 30°,
距离为 8 3n mile,货轮由 A 处向正北航行到 D 处时,再看灯塔 B 在南偏东 60°,求:
(1)A 处与 D 处的距离;
(2)灯塔 C 与 D 处的距离.(结果精确到 1n mile)
[解析] (1)在△ABD 中,∠ADB=60°,∠B=45°,
由正弦定理得
AD= ABsinB
sin∠ADB
=
12 6× 2
2
3
2
=24(n mile).
(2)在△ADC 中,由余弦定理得
CD2=AD2+AC2-2AD·ACcos30°,
解得 CD=8 3≈14(n mile).
即 A 处与 D 处的距离为 24n mile,灯塔 C 与 D 处的距离约为 14n mile.
13.某海域内一观测站 A,某时刻测得一艘匀速直线行驶的船只位于点 A 北偏东 50°且与 A 相距 80 海里的位置
B,经过 1 小时又测得该船已行驶到点 A 北偏东 50°+θ(其中 sinθ= 15
8
,0°<θ<90°)且与 A 相距 60 海里的位
置 C.
(1)求该船的行驶速度;
(2)若该船不改变航行方向继续向前行驶,求船在行驶过程中离观测站 A 的最近距离.
[解析] (1)如图,AB=80,AC=60,∠BAC=θ,sinθ= 15
8
.
由于 0°<θ<90°,所以 cosθ= 1-
15
8 2=7
8
.
由余弦定理得 BC= AB2+AC2-2AB·ACcosθ=40,
所以船的行驶速度为 40 海里/小时.
(2)在△ABC 中,由正弦定理得 BC
sin∠BAC
= AC
sin∠ABC
,
∴sin∠ABC=AC·sin∠BAC
BC
=60×
15
8
40
=3 15
16
,
自 A 作 BC 的垂线,交 BC 的延长线于 D,则 AD 的长是船离观测站的最近距离.
在 Rt△ABD 中,AD=ABsin∠ABD=80×3 15
16
=15 15(海里),
∴船在行驶过程中离观测站 A 最近距离为 15 15海里.
14.(2018·陕西理)如图 A,B 是海面上位于东西方向相距 5(3+ 3)海里的两个观测点,现位于 A 点北偏东 45°,
B 点北偏西 60°的 D 点有一艘轮船发出求救信号,位于 B 点南偏西 60°且与 B 点相距 20 3海里的 C 点的救援船立即
前往营救,其航行速度为 30 海里/小时,该救援船到达 D 点需要多长时间?
[解析] 本题考查正余弦定理在实际问题中的应用,本题要结合图像确定恰当三角形进行边角的求解,求解过程
中三角函数的变形,转化是易错点,注意运算的准确性.
由题意知 AB=5(3+ 3)海里,
∠DBA=90°-60°=30°,∠DAB=45°,∴∠ADB=105°
在△DAB 中,由正弦定理得, DB
sin∠DAB
= AB
sin∠ADB
∴DB=AB·sin∠DAB
sin∠ADB
=5 3+ 3· sin45°
sin105°
= 5 3+ 3· sin45°
sin45°·cos60°+sin60°·cos45°
=
5 3 3+1
3+1
2
=10 3(海里).
又∠DBC=∠DBA+∠ABC=30°+(90°-60°)=60°,
BC=20 3(海里),
在△DBC 中,由余弦定理得
CD2=BD2+BC2-2BD·BC·cos∠DBC=300+1200-2×10 3×20 3×1
2
=900,
∴CD=30(海里),
则需要的时间 t=30
30
=1(小时).
答:救援船到达 D 点需要 1 小时.
点评:(1)解决实际应用问题,要过好语言关,图形关和数理关,考生在平时训练中要注意加强.
(2)本题若认定△DBC 为直角三角形,由勾股定理正确求得 CD,同样可以.
15.(2018·福建文)某港口 O 要将一件重要物品用小艇送到一艘正在航行的轮船上.在小艇出发时,轮船位于港
口 O 北偏西 30°且与该港口相距 20 海里的 A 处,并正以 30 海里/小里的航行速度沿正东方向匀速行驶.假设该小船
沿直线方向以 v 海里/小时的航行速度匀速行驶,经过 t 小时与轮船相遇.
(1)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(2)为保证小艇在 30 分钟内(含 30 分钟)能与轮船相遇,试确定小艇航行速度的最小值.
(3)是否存在 v,使得小艇以 v 海里/小时的航行速度行驶,总能有两种不同的航行方向与轮船相遇?若存在,试
确定 v 的取值范围;若不存在,请说明理由.
[解析] 本小题主要考查解三角形,二次函数等基础知识,考查推理论证能力,抽象概括能力,运算求解能力,
应用意识,考查函数与方程思想,数形结合思想,化归与转化思想.
(1)设相遇时小艇的航行距离为 S 海里,则
S= 900t2+400-2·30t·20·cos 90°-30° = 900t2-600t+400= 900 t-1
3
2+300
故当 t=1
3
时,Smin=10 3,v=
10 3
1
3
=30 3.
即小艇以 30 3海里/小时的速度航行,相遇时小艇的航行距离最小.
(2)设小艇与轮船在 B 处相遇.
由题意可得:(vt)2=202+(30t)2-2·20·30t·cos(90°-30°)
化简得:v2=400
t2 -600
t
+900=400(1
t
-3
4
)2+675
由 00),
于是 400u2-600u+900-v2=0(*)
小艇总能有两种不同的航行方向与轮船相遇,等价于方程(*)应有两个不等正根,即:
6002-1600× 900-v2 >0
900-v2>0
解得 15 3
查看更多