- 2021-06-15 发布 |
- 37.5 KB |
- 3页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
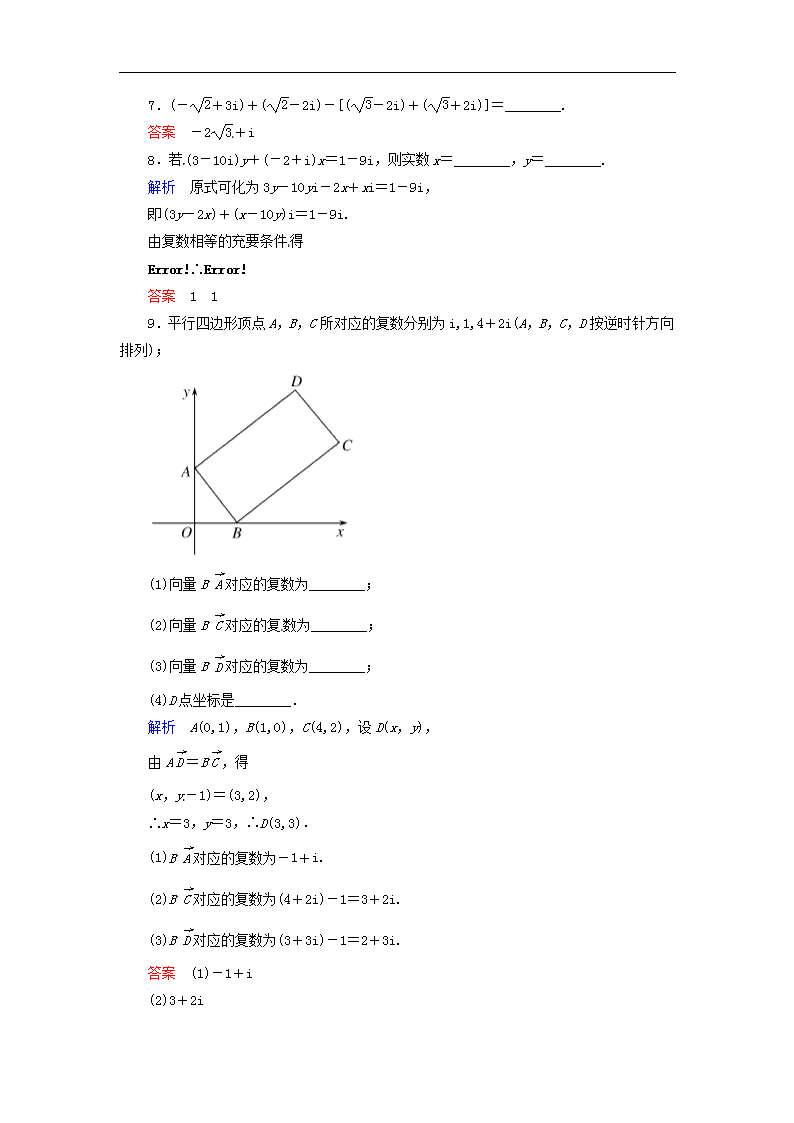
高中数学 3-2-1 复数代数形式的加、减运算及其几何意义双基限时训练 新人教版选修2-2
【名师一号】2014-2015学年高中数学 3-2-1 复数代数形式的加、减运算及其几何意义双基限时训练 新人教版选修2-2 1.已知复数z1=3+4i,z2=3-4i,则z1+z2=( ) A.8i B.6 C.6+8i D.6-8i 答案 B 2.(5-i)-(3-i)-5i等于( ) A.5i B.2-5i C.2+5i D.2 答案 B 3.已知复数z满足z+i-3=3-i,则z等于( ) A.0 B.2i C.6 D.6-2i 答案 D 4.|(3+2i)-(4-i)|等于( ) A. B. C.2 D.-1+3i 解析 |(3+2i)-(4-i)|=|-1+3i|=. 答案 B 5.复平面内两点Z1和Z2分别对应于复数3+4i和5-2i,那么向量对应的复数为( ) A.3+4i B.5-2i C.-2+6i D.2-6i 解析 =-,即终点的复数减去起点的复数,∴(5-2i)-(3+4i)=2-6i. 答案 D 6.复数z=x+yi(x,y∈R)满足条件|z-4i|=|z+2|,则2x+4y的最小值为( ) A.2 B.4 C.4 D.16 解析 |z-4i|=|x+(y-4)i|,|z+2|=|x+2+yi|,依题意得x2+(y-4)2=(x+2)2+y2,即x+2y=3.∴2x+4y=2x+22y≥2=2=4.当且仅当x=2y=时,取等号. 答案 C 7.(-+3i)+(-2i)-[(-2i)+(+2i)]=________. 答案 -2+i 8.若(3-10i)y+(-2+i)x=1-9i,则实数x=________,y=________. 解析 原式可化为3y-10yi-2x+xi=1-9i, 即(3y-2x)+(x-10y)i=1-9i. 由复数相等的充要条件得 ∴ 答案 1 1 9.平行四边形顶点A,B,C所对应的复数分别为i,1,4+2i(A,B,C,D按逆时针方向排列); (1)向量B对应的复数为________; (2)向量B对应的复数为________; (3)向量B对应的复数为________; (4)D点坐标是________. 解析 A(0,1),B(1,0),C(4,2),设D(x,y), 由A=B,得 (x,y-1)=(3,2), ∴x=3,y=3,∴D(3,3). (1)B对应的复数为-1+i. (2)B对应的复数为(4+2i)-1=3+2i. (3)B对应的复数为(3+3i)-1=2+3i. 答案 (1)-1+i (2)3+2i (3)2+3i (4)(3,3) 10.设z1=x+2i,z2=3-yi(x,y∈R),且z1+z2=5-6i,求x+yi. 解 ∵z1+z2=x+3+(2-y)i, 又z1+z2=5-6i, ∴∴ ∴x+yi=2+8i. 11.复平面内有A,B,C三点,点A对应复数2+i,向量对应复数1+2i,向量对应复数3-i,求C点在复平面内的坐标. 解 ∵=-,∴对应的复数为(3-i)-(1+2i)=2-3i. 设C(x,y),则由=-, 得2-3i=(x+yi)-(2+i).∴x+yi=4-2i. ∴x=4,y=-2,故C点在复平面内的坐标为(4,-2). 12.在复平面内A,B,C三点对应的复数分别为1,2+i,-1+2i. (1)求向量,,对应的复数; (2)判断△ABC的形状; (3)求△ABC的面积. 解 (1)∵=-, ∴对应的复数为(2+i)-1=1+i. 同理对应的复数为 (-1+2i)-(2+i)=-3+i. 对应的复数为(-1+2i)-1=-2+2i. (2)∵||=,||=,||=, ∴||2+||2=||2. ∴△ABC为直角三角形. (3)由(2)知,△ABC的面积为S△=××=2.查看更多