2020届二轮复习函数和对数函数课件（全国通用）

2020届二轮复习函数和对数函数课件（全国通用）

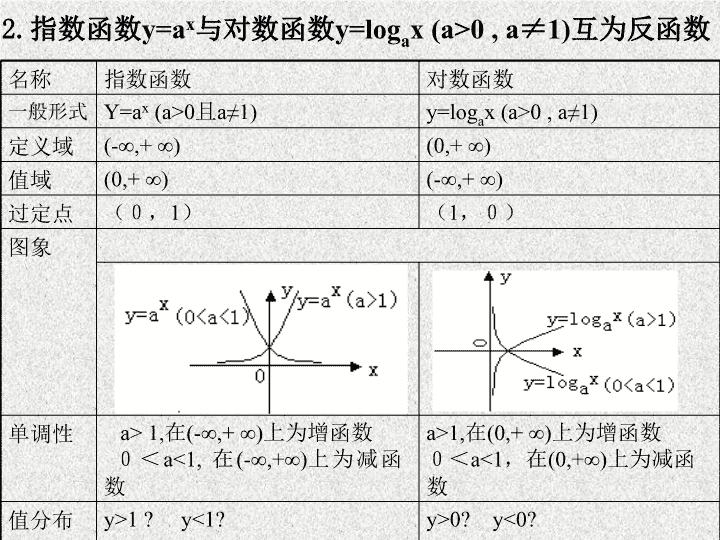
高三备课组 对数与对数函数 1．对数的内容 (1)对数的概念 如果 ,那么 b 叫做以 a 为底 N 的对数, 记 (2)对数的性质：①零与负数没有对数 ② ③ 一．基础知识 (4) 对数换底公式 (3)对数的运算性质 其中 a>0,a≠0,M>0,N>0 名称 指数函数 对数函数 一般形式 Y=a x (a>0 且 a≠1) y=log a x (a>0 , a≠1) 定义域 (-∞,+ ∞) (0,+ ∞) 值域 (0,+ ∞) (-∞,+ ∞) 过定点 （０，1） （1，０） 图象 单调性 a> 1, 在(-∞,+ ∞)上为增函数 ０＜ a<1, 在(-∞,+∞)上为减函数 a>1, 在(0,+ ∞)上为增函数 ０＜ a<1， 在(0,+∞)上为减函数 值分布 y>1 ? y<1? y>0? y<0? 2.指数函数 y=a x 与对数函数 y=log a x (a>0 , a ≠ 1) 互为反函数 3.记住下列特殊值为底数的函数图象 ： 　　　　　 1.指数函数 y=a 与对数函数 y=log x (a>0 , a≠1) 互为反函数，从概念、图象、性质去理解它们的区别和联系   4.几个注意点. 　　　　 2.研究对数函数问题，尽量化为同底，并注意对数问题中的定义域限制 二、题型剖析 1．对数式的化简和运算 例1.计算下列各式 ①书例1 ② 练习.计算 （1） （2） 2．换底公式及应用 例2（ 1 ）已知 （ 2 ）若 练习.已知 a 、 b 、 c 均是不等于 1 的正数， 且 ，求 abc 的值 3. 指对数互化 例3.已知 x,y,z 为正数，满足 1. 求证： 2. 比较 3 x 、 4y 、 6z 的大小 变式:已知 f(x)=a x ,g(x)=log a x(a>0,a≠1)， 若 f(3)×g(3)<0, 那么 f(x) 与 g(x) 在同一坐标系内的图象可能为（ ） 4. 对数函数的图象 例4．例书 P24 例2 5. 对数函数的图象 例5．例书 P24 例3 练习：已知 f(x)=log 4 (2x+3-x 2 ) 求（ 1 ） f(x) 的单调区间；（ 2 ）求函数 f(x) 的最大值及对应的 x 的值 . (3)求函数 在单调增区间上 的反函数 四、作业 优化设计 三、小结 1．对数式的运算、求值、化简、证明等问题主要依据对数的运算法则及换底公式加以解决。 2．指对数互化是解决有关指、对数问题的有效方法。 3 3.指数函数 与对数函数 y=log x (a>0 , a≠1) 互为反函数，从概念、图象、性质去理解它们的区别和联系，从而用性质和图象解题。