2020届二轮复习连续型随机变量学案(全国通用)
连续型随机变量
若随机变量X的分布函数F(X)可表示成一个非负可积函数f(x)的积分,则称X为连续随机变量.
连续型随机变量的概念
若随机变量 X 的分布函数 F(X) 可表示成一个非负可积函数 f(x) 的积分,则称 X 为连续型随机变量,f(x) 称为 X 的概率密度函数(分布密度函数).
正态分布
· 正态曲线的定义
如果随机变量 X 的概率密度函数为
φμ,σx=12πσe-x-μ22σ2, x∈-∞,+∞
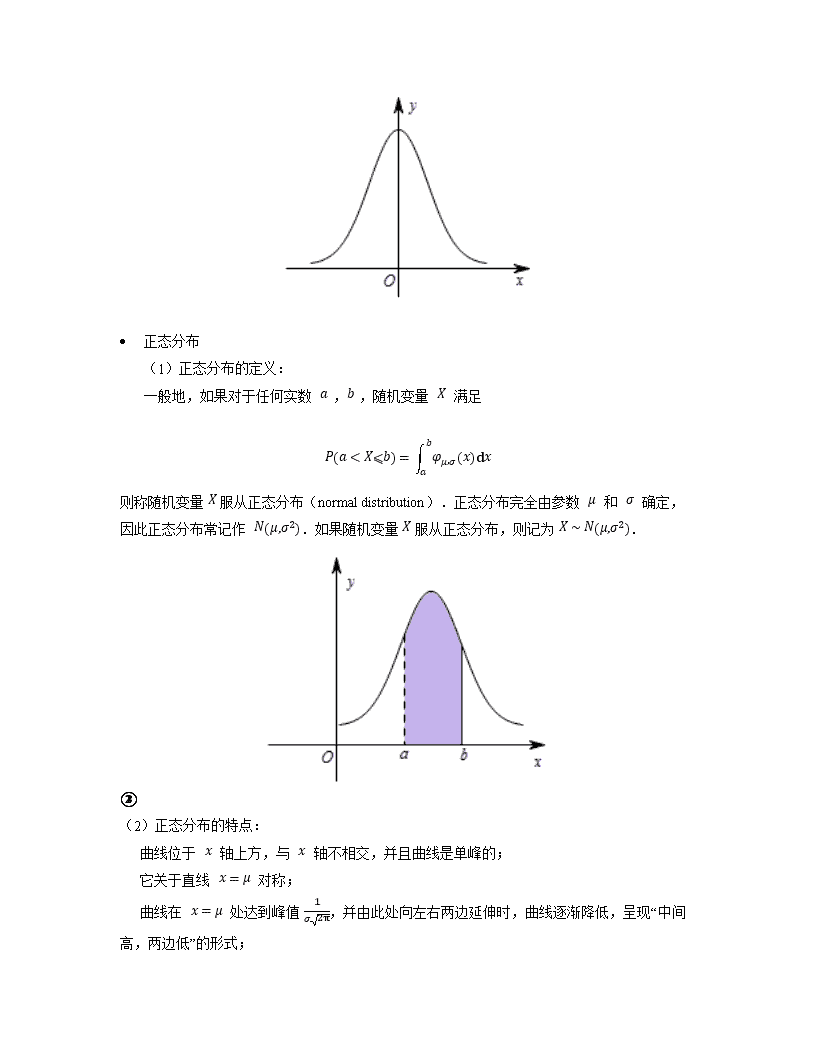
其中实数 μ 和 σ ( σ>0 )为参数.我们称 φμ,σx 的图象为正态分布密度曲线,简称正态曲线.
当 μ=0, σ=1 时,函数表达式是
fx=12πe-x22, x∈-∞,+∞
相应的曲线称为标准正态曲线.
· 正态分布
(1)正态分布的定义:
一般地,如果对于任何实数 a ,b ,随机变量 X 满足
Pa
0,Pμ-a3=0,158,则 Pξ>1=
【答案】 0.842
【分析】 因为随机变量 ξ∼N2,1,所以正态曲线关于 x=2 对称,
因为 Pξ>3=0.158,所以 Pξ>1=1-Pξ<1=1-0.158=0.842.
4. 正态曲线具有以下特点:
(1)曲线在 x 轴上方,与 x 轴 .
(2)曲线是单峰的,它关于直线 对称.
(3)曲线在 x=μ 处达到峰值 .
(4)曲线与 x 轴之间的面积为 .
(5)当 σ 一定时,曲线随着 μ 的变化沿 x 轴 .
(6)当 μ 一定时,曲线形状由 σ 确定,σ 越小,曲线越 .
【答案】 不相交;x=μ;1σ2π;1;平移;瘦高
5. 已知随机变量 X 服从正态分布 N1,σ2,若 P00 ,则 Pξ⩾b 的值是 (用 a 表示).
【答案】 1-a2
2. 在某项测量中,测量结果 X 服从正态分布 N1,σ2σ>0,若 X 在 0,1 内取值的概率为 0.4,则 X 在 0,2 内取值的概率为 .
【答案】 0.8
3. 如图是当 σ 取三个不同值 σ1,σ2,σ3 时的三种正态曲线 N0,σ2 的图象,那么 σ1,σ2,σ3 的大小关系是 .
【答案】 σ1<σ2<σ3
4. 已知正态分布 Nμ,σ2 的密度曲线函数是 fx=12πσe-x-μ22σ2,x∈-∞,+∞,给出以下四个命题:
①对任意 x∈-∞,+∞ 都有 fμ-x=fμ+x 成立;
②如果随机变量 X∼Nμ,σ2,且 Fx=PX2=p,则 P090 的学生比例是 .
【答案】 0.1585
【分析】 u-σ=60,u+σ=90,P6090=121-P60130 的概率为 121-0.6826=0.1587.
所以 ξ⩾90 的概率为 0.6826+0.1587=0.8413.
所以及格的人数为 54×0.8413≈45(人).
130 分以上的人数为 54×0.1587≈9(人).
7. 已知某车间正常生产的某种零件的尺寸满足正态分布 N27.45,0.052,质量检验员随机抽查了 10 个零件,测量得它们的尺寸如下:
27.34,27.49,27.55,27.23,27.40
27.46,27.38,27.58,27.54,27.68
请你根据正态分布的小概率事件,帮助质量检验员确定哪些应该判定为非正常状态下生产的零件.
【解】 根据小概率事件在一次试验中几乎不可能发生的思想,我们对落在区间 27.45-3×0.05,27.45+3×0.05 之外的零件尺寸做出拒绝接受零件是正常状态下生产的假设,有尺寸为 27.23 和 27.68 的两个零件不符合落在区间 27.45-3×0.05,27.45+3×0.05 内这一条件,判定它们就是在非正常状态下生产的.
8. 如图,面积为 S 的正方形 ABCD 中有一个不规则的图形 M,可按下面方法估计 M 的面积:在正方形 ABCD 中随机投掷 n 个点,若 n 个点中有 m 个点落入 M 中,则 M 的面积的估计值为 mnS,假设正方形 ABCD 的边长为 2,M 的面积为 1,并向正方形 ABCD 中随机投掷 10000 个点,以 X 表示落入 M 中的点的数目.
附表:Pk=t=0kC10000t×0.25t×0.7510000-t.
K2424242525742575Pk0.04030.04230.95700.9590
(1)求 X 的均值 EX;
【解】 根据题意知,每个点落在 M 内的概率是相同的为 14,
故 X∼B10000,14,根据二项分布期望公式知:
EX=10000×14=2500.
(2)求用以上方法估计 M 的面积时,M 的面积的估计值与实际值之差在区间 -0.03,0.03 内的概率.
【解】 依题意所求概率为 P-0.034=0.4,则 Pξ>0= .
3. 已知某电子元件的使用寿命(单位:小时)服从正态分布 N1000,502,那么该电子元件的使用寿命超过 1000 小时的概率为 .
4. 正态变量在 u-σ,u+σ 内取值的概率为 ,正态变量在 u-2σ,u+2σ 内取值的概率为 ,正态变量在 u-3σ,u+3σ 内取值的概率为 .
5. 在标准正态总体N0,1中 ,若 ϕ1=a,ϕ2=b ,则该总体在 1,2 内的概率为 .
6. 已知随机变量 ξ 服从正态分布 N2,σ2,Pξ⩽4=0.84,则 Pξ⩽0= .
7. 设在某次英语考试中,考生的分数 ξ∼N90,202,则得分在 70 分 ∼110 分的学生约占总人数的 .
8. 抽样调查表明,某校高三学生成绩(总分 750 分)近似服从正态分布,已知一次考试的平均成绩为 500 分,P4002= .
11. 某城市从南区某地乘公共汽车前往北区火车站有两条线路可走,第一条线路穿过市区,路线较短,但交通拥挤,所需时间(单位:min)服从正态分布 N50,102;第二条线路沿环城公路走,路程较长,但交通阻塞少,所需时间服从正态分布 N60,42.
(1)若只有 70min 可用,问应走哪条路线?
(2)若只有 60min 可用,问应走哪条路线?
12. 正态总体 N0,1 的概率密度函数是 fx=12πe-x22,x∈R.
(1)求证:fx 是偶函数;
(2)求 fx 的最大值;
(3)利用指数函数的性质说明 fx 的增减性.
13. 工厂制造的某机械零件尺寸 X 服从正态分布 N4,19,问在一次正常的试验中,取 1000 个零件时,不属于区间 3,5 这个尺寸范围的零件大约有多少个?
14. 一台机床生产一种尺寸为 10 mm 的零件,现在从中抽测 10 个,它们的尺寸分别如下(单位: mm ): 10.2,10.1,10,9.8,9.9,10.3,9.7,10,9.9,10.1 ,如果机床生产零件的尺寸 η 服从正态分布,求正态分布的概率密度函数表达式.
15. 若一个正态分布的概率密度函数是一个偶函数,且该函数的最大值为 142π.求该正态分布的概率密度函数的解析式.
16. 在某市组织的一次数学竞赛中全体参赛学生的成绩近似服从正态分布 N60,100,已知成绩在 90 分以上的学生有 13 人.
(1)求此次参加竞赛的学生总数共有多少人?
(2)若计划奖励竞赛成绩排在前 228 名的学生,问受奖学生的分数线是多少?
17. 一批电池(一节)用于手电筒的寿命服从均值为 35.6 小时、标准差为 4.4 小时的正态分布,随机从这批电池中任意取一节,问这节电池可持续使用不少于 40 小时的概率是多少?
18. 是否存在常数 μ,σσ>0 使得随机变量 ξ 服从正态分布 Nμ,σ2 ,且同时满足 Pξ<0.5=0.0778,Pξ⩾1.5=0.7611 ;若不存在,说明理由;若存在,试求 P0.6<ξ<1.2 的值.
19. 设在一次数学考试中,某班学生的分数 X∼N110,202,且知试卷满分 150 分,这个班的学生共 54 人,求这个班在这次数学考试中及格(即 90 分以上)的人数和 130 分以上的人数.
20. 在标准正态总体 N0,1 下,定义 Φx0 表示随机变量 X 取值小于 x0 的概率,即 Φx0=PX<x0(x0⩾0).某正态随机变量 X 的概率密度函数是偶函数,而且该函数的最大值为 12π,试用 Φ0.2,Φ1.2 表示随机变量 X 落入区间 -1.2,0.2 之间的概率.
连续型随机变量-出门考
姓名 成绩
1. 设随机变量 ξ∼N2,22,则 D12ξ= .
2. 一个随机变量如果是 、 、 偶然因素作用之和,它就服从或近似服从正态分布.
3. 某种零件的尺寸服从正态分布 N0,22,则不属于区间 -4,4 范围的零件约占总数的 .
4. 设随机变量 ξ 服从正态分布 N0 ,1,a>0 ,则下列结论正确的是 .
① P∣ξ∣a
5. 设随机变量 ξ 服从正态分布 N0,1,记 Φx=Pξ-1=34,则 Pξ>5= .
8. 已知 ξ 服从正态分布 N5,8 ,则 η=ξ-3 服从 .
9. 设随机变量 X 满足正态分布 X∼N-1,σ2,若 P-3⩽x⩽-1=0.4,则 P-3⩽x⩽1= .
10. 设随机变量 ξ 服从正态分布 N2,9,若 Pξ>c+2=Pξ0.1.
13. 某年级的一次信息技术测验成绩近似服从正态分布 N70,102,如果规定低于 60 分为不及格,求:
(1)成绩不及格的人数占多少?
(2)成绩在 80∼90 内的学生占多少?
14. 在某校举行的数学竞赛中,全体参赛学生的竞赛成绩近似服从正态分布 N70,100.已知成绩在 90 分以上(含 90 分)的学生有 12 名.
(1)试问此次参赛的学生总数约为多少人?
(2)若该校计划奖励竞赛成绩排在前 50 名的学生,试问设奖的分数约为多少分?
可供查阅的(部分)标准正态分布表 Φx0=Px<x0:
x001234567891.20.88490.88690.88880.89070.89250.89440.89620.89800.89970.90151.30.90320.90490.90660.90820.90990.91150.91310.91470.91620.91771.40.91920.92070.92220.92360.92510.92650.92780.92920.93060.93191.90.97130.97190.97260.97320.97380.97440.97500.97560.97620.97672.00.97720.97780.97830.97880.97930.97980.98030.98080.98120.98172.10.98210.98260.98300.98340.98380.98420.98460.98500.98540.9857
15. 某校高中二年级期末考试的物理成绩 ξ 服从正态分布 N70,102.
(1)若参加考试的学生有 100 人,学生甲得分为 80 分,求学生甲的物理成绩排名;
(2)若及格(60 分及其以上)的学生有 101 人,求第 20 名的物理成绩.已知标准正态分布表 φ0.97=0.833.
16. 设正态总体落在区间 -∞,-1 和区间 3,+∞ 内的概率相等,落在区间 -2,4 内的概率为 99.74% ,求该正态总体对应的正态曲线的最高点的坐标.
17. 对于正态曲线 fx=102πe-50x-12 与标准的正态曲线 gx=12πe-x22 解答下列问题:
(1)求两个正态总体的均值与方差.
(2) fx 的图象可由 gx 的图象经过怎样的平移和伸缩变换得到?
18. 如果随机变量 ξ∼Nμ,σ2,Eξ=Dξ=1,求 P-1<ξ<1 的值.
19. 美军轰炸机向巴格达某铁路控制枢纽投弹,炸弹落弹点与铁路控制枢纽的距离 x 的密度函数为 fx=100-∣x∣10000,∣x∣⩽1000,∣x∣>100,若炸弹落在目标 40 米以内时,将导致该铁路枢纽破坏,已知投弹 3 颗,求巴格达铁路控制枢纽被破坏的概率.
20. 为了监控某种零件的一条生产线的生产过程,检验员每天从该生产线上随机抽取 16 个零件,并测量其尺寸(单位:cm).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布 N(μ,σ2).
(1)假设生产状态正常,记 X 表示一天内抽取的 16 个零件中其尺寸在 (μ-3σ,μ+3σ) 之外的零件数,求 P(X⩾1) 及 X 的数学期望;
(2)一天内抽检零件中,如果出现了尺寸在 (μ-3σ,μ+3σ) 之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
(i)试说明上述监控生产过程方法的合理性;
(ii)下面是检验员在一天内抽取的 16 个零件的尺寸:
9.9510.129.969.9610.019.929.9810.0410.269.9110.1310.029.2210.0410.059.95
经计算得 x=116i=116xi=9.97,s=116i=116(xi-x)2=116(i=116xi2-16x2)≈0.212,其中 xi 为抽取的第 i 个零件的尺寸,i=1,2,⋯,16.
用样本平均数 x 作为 μ 的估计值 μ,用样本标准差 s 作为 σ 的估计值 σ,利用估计值判断是否需对当天的生产过程进行检查?剔除 (μ-3σ,μ+3σ) 之外的数据,用剩下的数据估计 μ 和 σ(精确到 0.01).
附:若随机变量 Z 服从正态分布 N(μ,σ2),则 P(μ–3σ
查看更多