- 2021-06-15 发布 |
- 37.5 KB |
- 5页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2018-2019学年贵州省遵义航天高级中学高二上学期期中考试数学(文)试题(Word版)
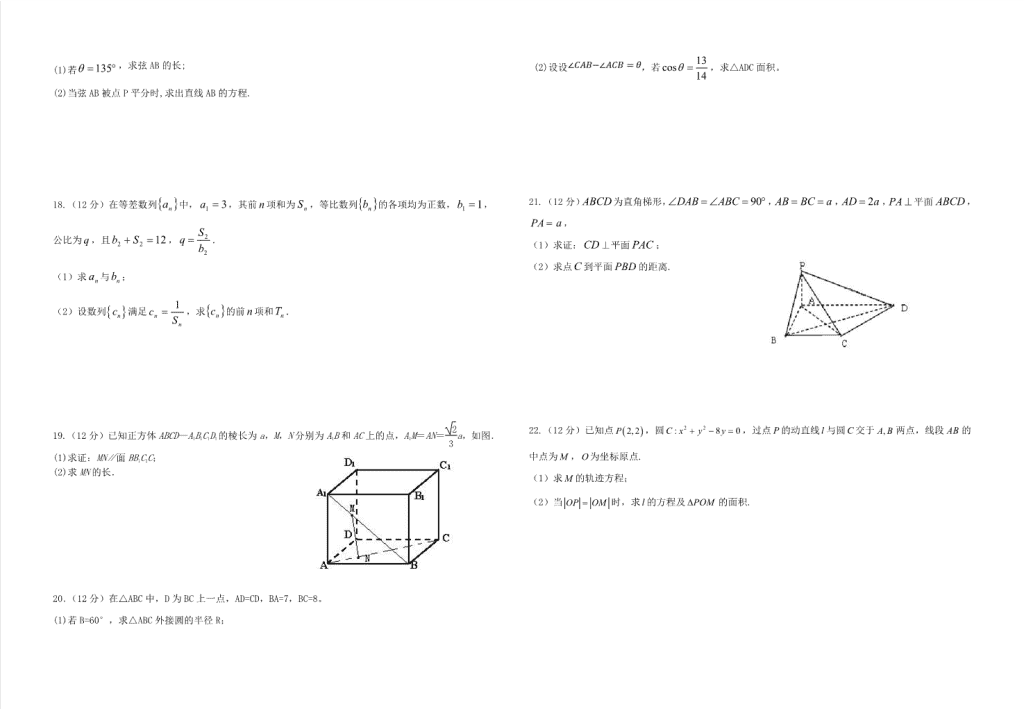
2018-2019 学年贵州省遵义航天高级中学高二上学期期中考试 数 学(文科) 一.选择题。(每题 5 分) 1.点 P(a,b,c)到坐标平面 xOy 的距离是( ) A. a2+b2 B.|a| C.|b| D.|c| 2.过两点 )3,2(),,4( ByA 的直线的倾斜角为 45 ,则 y ( ) A. 2 3 B. 2 3 C. 1 D. 1 3.直线 3x+4y=b 与圆 2 2 2 2 1 0x y x y 相切,则 b=( ) A. -2 或 12 B. 2 或-12 C.-2 或-12 D.2 或 12 4.已知 m , n 为两条不同的直线, , 为两个不同的平面,则下列命题中正确的是( ) A. ////,//,, nmnm B. nmnm //,,// C. //, nnmm D. mnmn ,// 5.等差数列{ }na 中, 1 4 7 39a a a , 3 6 9 27a a a ,则数列{ }na 的前 9 项的和 S9 等于( ) A.99 B. 66 C.144 D.297 6.直线(a+2)x+(1-a)y-3=0 与(a-1)x+(2a+3)y+2=0 互相垂直,则 a 等于( ) A.-1 B.1 C.±1 D.-3 2 7.一只蚂蚁在边长分别为 3,4,5 的三角形区域内随机爬行,则其恰在离三个顶点距离都大于 1 的地方的 概率为( ) A. B.1﹣ C.1﹣ D.1﹣ 8、一个直棱柱被一个平面截去一部分后所剩几何体的三视图如图所示, 则该 几何体的体积为( ) A. 9 B. 10 C. 11 D. 12 9.已知,,,则的取值范围是( ) A. B. C. D. 10.在正四面体 ABCD 中,E,F 分别为 AB,CD 的中点,则 EF 与 AC 所成角为( ) A.90° B.60° C.45° D.30° 11. 若圆 222 )5()3( ryx 上有且只有两个点到直线 0234 yx 的距离等于 1,则半径 r 的取 值范围是( ) A.(4,6) B.[4,6] C.(4,5) D.(4,5] 12.已知 QP, 分别是直线 02: yxl 和圆 1: 22 yxC 上的动点,圆 C 与 x 轴正半轴交于点 )0,1(A ,则 PQPA 的最小值为( ) A. 15 B. 2 C. 2 D. 12 102 二.解答题。(每空 5 分) 13.若 ,x y 满足约束条件 0 2 0 0 x y x y y ,则 3 4z x y 的最小值为__________. 14.若曲线 21 xy 与直线 bxy 始终有两个交点,则b 的取值范围是________. 15.三棱锥 P ABC 中, 2, 2 2, 2 3PA AB BC PB AC PC ,则三棱锥 P ABC 的外接 球的表面积为__________. 16.如图,矩形 ABCD 中, 2 4AB AD , E 为边 AB 的中点,将 ADE 沿直线 DE 翻转成 1A DE , 构成四棱锥 1A BCDE ,若 M 为线段 1AC 的中点,在翻转过程中有如下四个命题: ① / /MB 平面 1A DE ; ②存在某个位置,使 1DE AC ; ③存在某个位置,使 1A D CE ; ④点 1A 在半径为 2 的圆周上运动: 其中正确的命题是__________. 三.解答题。 17.(10 分)已知圆 2 2x y =9 内有一点 P(-1,2),AB 为过点 P 的弦且倾斜角为 . (1)若 135 ,求弦 AB 的长; (2)当弦 AB 被点 P 平分时,求出直线 AB 的方程. 18.(12 分)在等差数列 na 中, 31 a ,其前 n 项和为 nS ,等比数列 nb 的各项均为正数, 11 b , 公比为 q ,且 1222 Sb , 2 2 b Sq . (1)求 na 与 nb ; (2)设数列 nc 满足 n n Sc 1 ,求 nc 的前 n 项和 nT . 19.(12 分)已知正方体 ABCD—A1B1C1D1 的棱长为 a,M,N 分别为 A1B 和 AC 上的点,A1M=AN= 2 3 a,如图. (1)求证:MN∥面 BB1C1C; (2)求 MN 的长. 20.(12 分)在△ABC 中,D 为 BC 上一点,AD=CD,BA=7,BC=8。 (1)若 B=60°,求△ABC 外接圆的半径 R; (2)设设 ,若 14 13cos ,求△ADC 面积。 21.(12 分)ABCD 为直角梯形, 90DAB ABC ,AB BC a , 2AD a ,PA 平面 ABCD , PA a , (1)求证:CD ⊥平面 PAC ; (2)求点C 到平面 PBD 的距离. 22.(12 分)已知点 2,2P ,圆 2 2: 8 0C x y y ,过点 P 的动直线 l 与圆 C 交于 ,A B 两点,线段 AB 的 中点为 M ,O为坐标原点. (1)求 M 的轨迹方程; (2)当 OP OM 时,求 l 的方程及 POM 的面积. 高二文数答案 一、选择题 1-5 DCDDA 6-10 CDCDC 11-12 AA 二、填空题 13.-1 14. 15. 16. ƒ④ 三.解答题 17.(1)解: 设 A(x1,y1),B(x2,y2), 依题意:直线 AB 的斜率为-1 所以直线 AB 的方程为 x+y-1=0,联立直线方程与圆的方程得: x2-x-4=0,则 x1+x2= - 1 , x1x2= - 4 由弦长公式得 AB= (2)设直线 AB 的斜率为 k. 则直线 AB 的方程为 y-2=k(x+1) ; 因为 P 为 AB 的中点,则 OP 丄 AB 由斜率公式易求得直线 OP 斜率为-2,则-2k=-1,k= 所以,直线 AB 的方程为:x-2y+5=0 18.解:(Ⅰ)设 的公差为 , 因为 所以 解得 或 (舍), . 故 , . (Ⅱ)因为 ,所以 . 故 19.解 (1)证明:作 NP⊥AB 于 P,连接 MP.NP∥BC, ∴ AP AB= AN AC= A1M A1B, ∴MP∥AA1∥BB1, ∴面 MPN∥面 BB1C1C. MN⊂面 MPN, ∴MN∥面 BB1C1C. (2) NP BC= AN AC= a a= 1 3,NP= 1 3a, 同理 MP= 2 3a. 又 MP∥BB1, ∴MP⊥面 ABCD,MP⊥PN. 在 Rt△MPN 中 MN= 1 a2= 5 3a. 20.(1) 在△ABC 中,由余弦定理得 , 所以 , 由正弦定理得 , 所以 . 故△ABC 外接圆的半径 R 为 . (2)由 AD=CD,得∠DCA=∠DAC, 所以 . 所以 . 设 BD= ,则 DC=8 ,DA=8 . 在△ABD 中, , 由余弦定理得 , 得 . 所以 BD=3,DA=5, 由正弦定理得 ,即 , 所以 . 所以 故 .] 21.(1) 证明:取 中点为 ,连接 ,则 为正方形 ∴ 又 ∵ ,∴ 中有 ,即 ∵ 平面 , 平面 ∴ ,又 ∴ ⊥平面 (2)解:设点 到平面 的距离为 ,点 到平面 的距离为 ∵ ∴ 22.(1)圆 的方程可化为 ,所以圆心为 ,半径为 4. 设 ,则 , 由题设知 ,故 , 即 .由于点 在圆 的内部, 所以 的轨迹方程是 (2)由(1)可知 的轨迹是以点 为圆心, 为半径的圆. 由于 ,故 在线段 的垂直平分线上, 又 在圆 上,从而 . 因为 的斜率为 3,所以 的斜率为 ,故 的方程为 又 , 到 的距离为 ,所以 , ,故 的面积为 .查看更多