数学文卷·2017届山西省临汾一中、忻州一中、长治二中等五校高三上学期第五次联考(期末)(2017
2016~2017年度高三第五次联合考试(期末)
数学试卷(文科)
第I卷
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是
符合题目要求的.)
1.已知集合A={-1,0,l,2,3,4),B={x|x2<16,z∈N),则A B等于
A.{一1,0,1,2,3) B.{0,1,2,3,4) C.{1,2,3} D.{0,l,2,3)
2.复数的共轭复数在复平面内对应的点位于
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.变量x,y之间的一组相关数据如下表所示:
若x,y之间的线性回归方程为 =x+12. 28,则的值为
A. -0. 92 B. -0. 94 C. -0. 96 D. -0. 98
4.在平行四边形ABCD中,AB=3,AD=4,则等于
A.-7 B.1 C.7 D.25
5.在我国明代数学家吴敬所著的《九章算术比类大全》中,有一道数学名题叫“宝塔装灯”,内容为“远望巍巍塔七层,红灯点点倍加增;共灯三百八十一,请问顶层几盏灯?”(“倍加增”指灯的数量从塔的顶层到底层按公比为2的等比数列递增).根据此诗,可以得出塔的顶层和底层共有
A.3盏灯 B.192盏灯 C.195盏灯 D.200盏灯
6.执行如图所示的程序框图,若输出的k=8,则输入的k为
A.0
B.1
C.2
D.3
7.某几何体的三视图如图所示,则该几何体的表面积为
A. 8(+1)+ B.8(+1)+2
C.8(+1)一 D.8(+l)
8.将函数y=cos(2x+)的图象向左平移个单位后,得到f(x)的图象,则
A.f(x)=-sin 2x
B.f(x)的图象关于x= 一对称
C. f()=
D.f(x)的图象关于(1,0)对称
9.已知奇函数f(x)满足f(x一2)=f(x),当0
0,b>0)的右支上一点,A为右顶点,O为坐标原点,
若∠AOB=60°,则该双曲线的渐近线方程为
A.y=± B.y=± C.y=± D.y=±
11.已知三棱锥A- BCD内接于球O,且BC= BD=CD=2,若三棱锥A- BCD体积的最大值为4,则球O的表面积为
A.16 B.25 C.36 D.64
12.已知定义在R上的偶函数f(x)在[0,+∞)上递减,若不等式2f(-ax+lnx+1)+f(ax-lnx-1)≥3f(l)对x∈[1,3]恒成立,则实数a的取值范围是
A.[2,e] B. [ ,+∞) C.[,e] D.[,]
第Ⅱ卷
二、填空题(本大题共4小题,每小题5分,共20分,把答案填在答题卡中的横线上.)
13.抛物线x2=一10y的焦点在直线2mx+my+1=0上,则m=
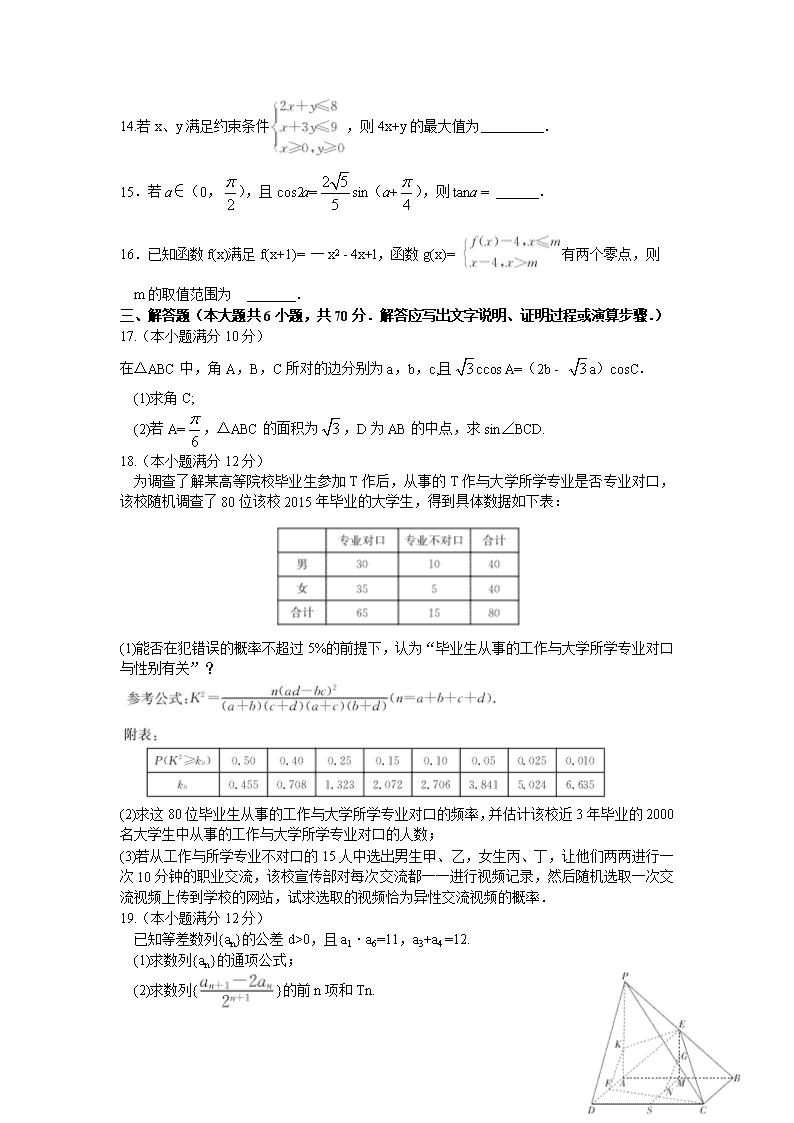
14.若x、y满足约束条件,则4x+y的最大值为 .
15.若a∈(0,),且cos2a=sin(a+),则tana = .
16.已知函数f(x)满足f(x+1)= 一x2 - 4x+l,函数g(x)= 有两个零点,则
m的取值范围为 .
三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
17.(本小题满分10分)
在△ABC中,角A,B,C所对的边分别为a,b,c,且ccos A=(2b - a)cosC.
(1)求角C;
(2)若A=,△ABC的面积为,D为AB的中点,求sin∠BCD.
18.(本小题满分12分)
为调查了解某高等院校毕业生参加T作后,从事的T作与大学所学专业是否专业对口,该校随机调查了80位该校2015年毕业的大学生,得到具体数据如下表:
(1)能否在犯错误的概率不超过5%的前提下,认为“毕业生从事的工作与大学所学专业对口与性别有关”?
(2)求这80位毕业生从事的工作与大学所学专业对口的频率,并估计该校近3年毕业的2000名大学生中从事的工作与大学所学专业对口的人数;
(3)若从工作与所学专业不对口的15人中选出男生甲、乙,女生丙、丁,让他们两两进行一次10分钟的职业交流,该校宣传部对每次交流都一一进行视频记录,然后随机选取一次交流视频上传到学校的网站,试求选取的视频恰为异性交流视频的概率.
19.(本小题满分12分)
已知等差数列{an}的公差d>0,且a1·a6=11,a3+a4 =12.
(1)求数列{an}的通项公式;
(2)求数列{}的前n项和Tn.
20.(本小题满分12分)
在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为矩形,
点E、F、M、S分别为棱PB、AD、AB、CD的中点,G为线段EM
的中点,且PA=AB=2AD=4,N为SM上一点,且NG∥平面CEF.
(1)确定N的位置,并求线段NG的长;
(2)平面CEF与PA交于点K,求三棱锥B-CKN的体积.
21.(本小题满分12分)
已知a∈R,函数f(x)=x3-ax2+ax+a,g(x)=f(x)+(a-3)x.
(1)求证:曲线y=f(x)在点(1,f(1))处的切线过点(2,4);
(2)若g(1)是g(x)在区间(0,3]上的极大值,但不是最大值,求实数a的取值范围.
21.(本小题满分12分)
设点F为椭圆C:=1(m>0)的左焦点,直线y=x被椭圆C截得的弦长为.
(1)求椭圆C的方程;
(2)圆P:(x+)2+(y一)2=r2(r>0)与椭圆C交于A,B两点,M为线段AB上任一点,直线FM交椭圆C于P,Q两点,若AB为圆P的直径,且直线FM的斜率大于1,求的取值范围.