数学理卷·2018届江西省崇仁二中高三上学期第四次月考（2017

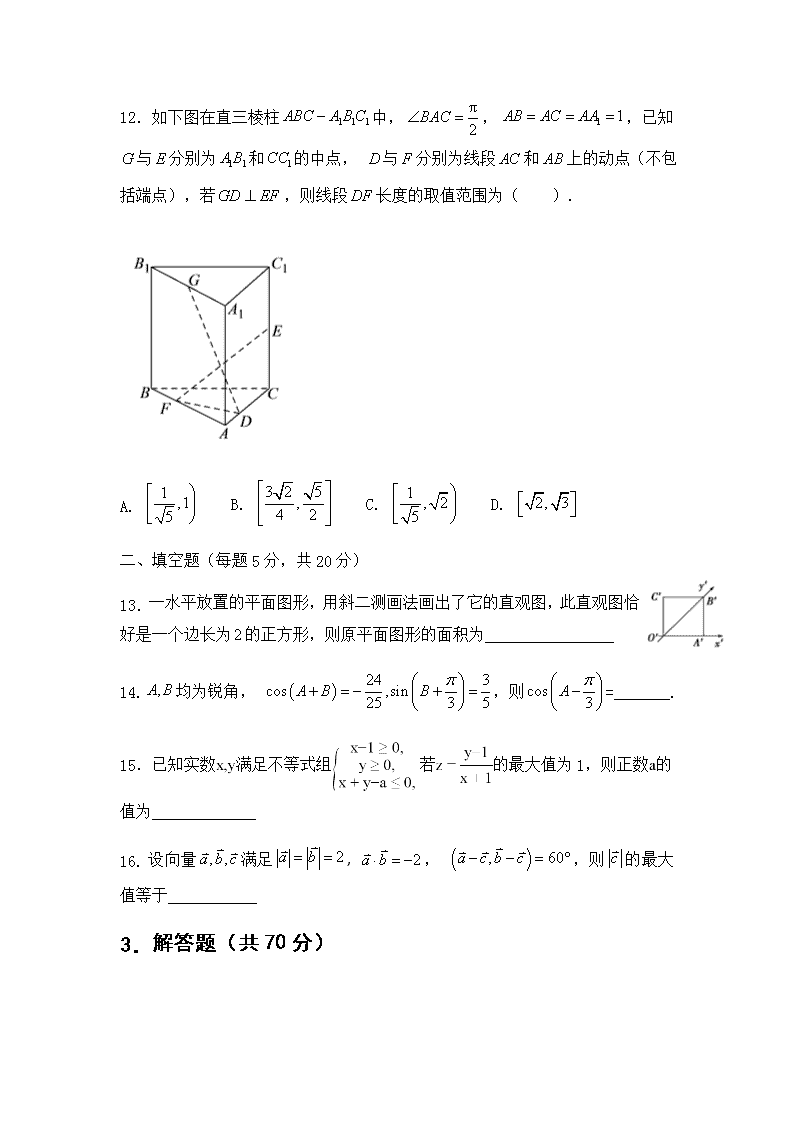
数学理卷·2018届江西省崇仁二中高三上学期第四次月考（2017

高三第四次月考数学（理）考试试卷 一．选择题（每题只有一个正确的选项，每个选项5分，共60分）‎ ‎1．设全集，集合， ，则（ ）‎ ‎ A. B. C. D. ‎ ‎2．设，则（ ）‎ ‎ A. 2i B. ‎2 C. 0 D. 1+i ‎3．“”是“函数在区间内单调递减”的（ ）‎ ‎ A. 必要不充分条件 B. 充分不必要条件 ‎ C. 充分必要条件 D. 既不充分也不必要条件 ‎4．已知向量.若,则实数（ ）‎ ‎ A. B. C. D. ‎ ‎5．在中，若， ，则（ ）‎ ‎ A. 1 B. C. D. ‎ ‎6．在长方体中，已知， ， ，‎ ‎ 若长方体的各顶点均在同一球面上，则该球的体积为（ ）．‎ ‎ A. B. C. D. ‎ ‎7．已知成等差数列， 成等比数列， 则的值是（ ）‎ ‎ A. B. C. 或 D. ‎ ‎8．函数f(x)＝3x＋x－2的零点所在的一个区间是(　　)‎ ‎ A. (－2，－1) B. (－1,0) C. (0,1) D. (1,2)‎ ‎9．已知函数，为得到函数的图象，可以将的图象（ ）‎ A. 向左平移个单位长度 B. 向左平移个单位长度 C. 向右平移个单位长度 D. 向右平移个单位长度 ‎10．若、n是互不相同的空间直线，α、β是不重合的平面，则下列命题中为真命题的是（ ）‎ A. 若，则 B. 若，则 C. 若则 D. 若，则 ‎11．已知正实数a，b满足，则的最小值（　　）‎ ‎ A. 1 B. C. D. ‎ ‎12．如下图在直三棱柱中， ， ，已知与分别为和的中点， 与分别为线段和上的动点（不包括端点），若，则线段长度的取值范围为（ ）.‎ A. ‎ B. C. D. ‎ 二、填空题（每题5分，共20分）‎ 13． 一水平放置的平面图形，用斜二测画法画出了它的直观图，此直观图恰好是一个边长为的正方形，则原平面图形的面积为 ‎ ‎14.均为锐角， ，则=_______.‎ ‎15．已知实数满足不等式组若的最大值为1，则正数的值为 ‎ 16. 设向量满足, ， ，则的最大值等于 ‎ 3． 解答题（共70分）‎ ‎17.（10分）已知数列是公比为2的等比数列，且成等差数列． 求数列的通项公式； 记，求数列的前n项和． 18.（12分）在中，内角所对的边分别为，已知． 求B； 若，求的面积． 19.（12分）已知数列的前n项和为，且， 求数列的通项公式； 若，设数列的前n项和为，证明． ‎ ‎20.（12分）如图，在四棱锥中，底面ABCD是矩形，平面以BD的中点O为球心、BD为直径的球面交PD于点M． 求证：平面ABM； 求直线PC与平面ABM所成的角的正切．‎ ‎ ‎ ‎21.（12分）如图，在直三棱柱中，是BC中点． 求证：平面； 在棱上存在一点M，满足，求平面与平面所成锐二面角的余弦值． ‎ ‎ 22.（12分）设函数． Ⅰ求函数的单调区间； Ⅱ记过函数两个极值点的直线的斜率为，问函数是否存在零点，请说明理由． ‎ ‎高三第四次月考数学（理）考试试卷答案 1． 选择题：（每题5分共60分）‎ ‎1.A 2.B 3.B 4.C 5.D 6.D 7.A 8.C 9.A 10.D ‎ 11.C 12.A 二：填空题：（每题5分共20分）‎ ‎ 13. 14. 15.4 16.4‎ 三：解答题：‎ 17. ‎（10分）‎ 解：（Ⅰ）由题意可得2（a3+1）=a2+a4，  即2（‎2a2+1）=a2+‎4a2，解得：a2=2．  ∴a1==1．  ∴数列{an}的通项公式为an=2n-1．  （Ⅱ）bn=an+log2an+1=2n-1+n，  Tn=b1+b2+b3+…+bn=（1+2+3+…+n）+（20+21+22+…+2n-1）  =  =．‎ 18. ‎（12分）‎ 解：（1）根据题意，atanB=2bsinA⇒a=2bsinA⇒asinB=2bsinAcosB，  由正弦定理可得sinAsinB=2sinBsinAcosB，  变形可得2cosB=1，即cosB=‎ ‎，  又由0＜B＜π，  故B=，  （2）由（1）可得：B=，  则C=π--=，  由正弦定理=，可得c=×sinC=，  S△ABC=bcsinA=×××=． 19.（12分）‎ ‎ 解：（1）当n=1时，得a1=1，  当n≥2时，得an=3an-1，  所以，  （2）由（1）得：，  又①  得②  两式相减得：，  故，  所以Tn=-． 20.(12分）‎ 证明：依题设，M在以BD为直径的球面上，则BM⊥PD．  因为PA⊥平面ABCD，  则PA⊥AB，又AB⊥AD，AD∩PA=A，  所以AB⊥平面PAD，  则AB⊥PD，AB∩BM=B，  因此有PD⊥平面ABM．  （2）解：设平面ABM与PC交于点N，  因为AB∥CD，所以AB∥平面PCD，  则AB∥MN∥CD，  由（1）知，PD⊥平面ABM，则MN是PN在平面ABM上的射影，  所以∠PNM就是PC与平面ABM所成的角，  且∠PNM=∠PCD，  tan．  故直线PC与平面ABM所成的角的正切值为2． ‎ 21. ‎(12分）‎ 证明：（1）连结A‎1C交AC1于点O，连结EO，  ∵ACC‎1A1是正方形，∴O为A‎1C的中点，  又E为CB的中点，∴EO∥A1B，  ∵EO⊂平面AEC1，A1B⊄平面AEC1，  ∴A1B∥平面AEC1．  解：（2）以A为原点，AB为x轴，AC为y轴，AA1为z轴，建立空间直角坐标系，  则A（0，0，0），B（2，0，0），B1（2，0，2），C（0，2，0），C1（0，2，2），E（1，1，0），  设M（0，0，m），（0≤m≤2），则=（-2，0，m-2），=（1，-1，-2），  ∵B‎1M⊥C1E，∴=-2-2（m-2）=0，解得m=1，  ∴M（0，0，1），=（1，1，-1），=（0，2，1），  设平面MEC1的法向量 ‎=（x，y，z），  则，取y=-1，得=（3，-1，2），  ∵AC⊥平面ABB‎1A1，∴取平面ABB‎1A1的法向量为=（0，2，0），  ∴cos＜＞==-，  ∴平面MEC1与平面ABB‎1A1所成锐二面角的余弦值为．‎ ‎22.(12分） 解：（Ⅰ），x＞0，求导，  令y′=0，解得：x=，或x=2，  当y′＞0，解得：0＜x＜，或x＞2，当y′＜0，解得：＜x＜2，…（3分）  ∴函数y=‎2f（x）‎-5g（x）在上递增，在上递减，在（2，+∞）上递增．…（5分）  （Ⅱ），，  设p（x）=x2-mx+1，设两个极值点A（x1，y1），B（x2，y2），…（6分）  ∵函数有两个大于零极值点，  ∴△=m2-4＞0，得m＞2且x1+x2=m，x1x2=1，  AB斜率=…（8分）  ，  由题意函数存在零点即有解，两根均为正且x1x2=1，…（9分）  若x1＜x2，则0＜x1＜1，x2＞1，消元得整理得  令，则，  ∴q（x）在区间（1，+∞）上单调递增，  ∴q（x）＞q（1）=0，  ∴函数y=h（m）+‎2m-2没有零点．…（12分）‎ ‎ ‎